To make a later integration valid, we have to name the semi-axes of the ellipsoid c > a > b > 0, so that b < c and
The Surface Area Of An Ellipsoid
A. Dieckmann, Universität Bonn, July 2003
This short note shows a way to the formula for the surface area of an ellipsoid. The result is given for example in the formula gallery of the Mathematica Book (Ref. 1), but with a typo. There was no instruction accessible to me, how it is obtained, and I had to try for myself. It proved harder than I first thought, so I think it is worthwhile to put the derivation on the internet.
To make a later integration valid, we have to name the semi-axes of the ellipsoid c > a > b > 0, so that b < c and ![]() The axes may be renamed at the end.
The axes may be renamed at the end.
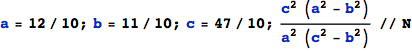
![]()
Now calculate the area numerically – for reference:
![]()
![]()
Symmetry allows the reduction of the integration domain:

![]()
Integrate symbolically with respect to θ :
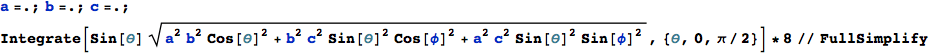
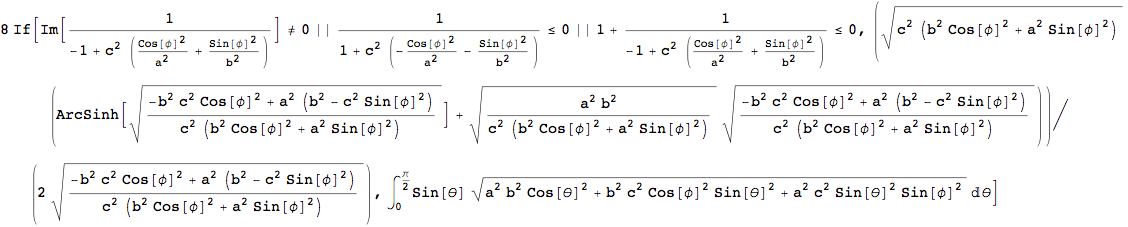
After numerical integration with respect to φ the area comes out correctly:

![]()
Express ArcSinh by ArcTanh:

![]()
![]()
And the integral can be reduced to a simpler form by substituting ![]()
![]()
![]()
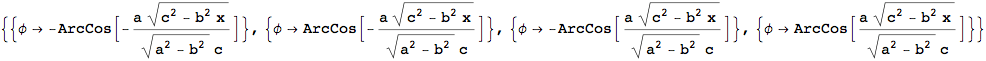
The Jacobian dφ/dx is:
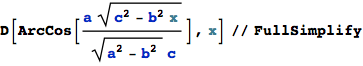
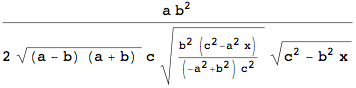
Check the new, 'simple' form :
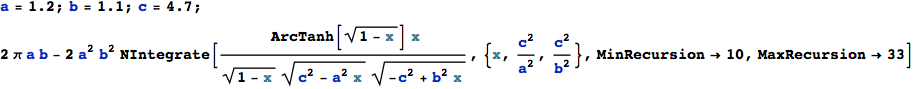
![]()
Then integrate by parts with ![]()
![]()
![]()
![]()
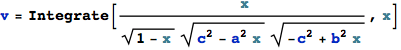
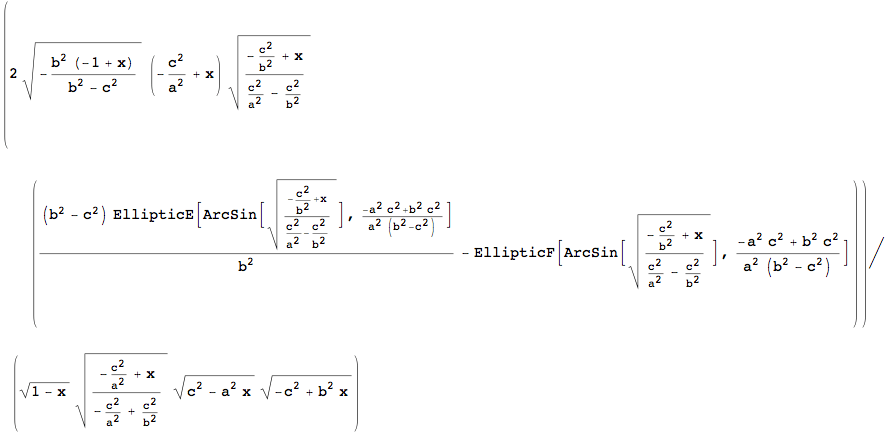
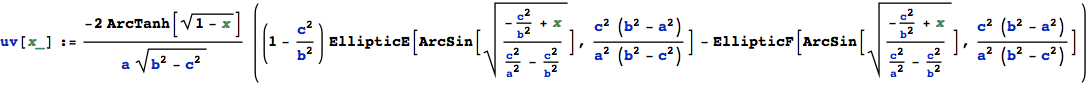
![]()
![]()
uv(upper limit) - uv(lower limit):
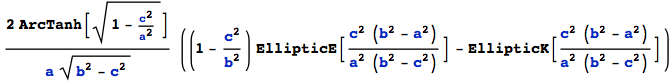
![]()
![]()
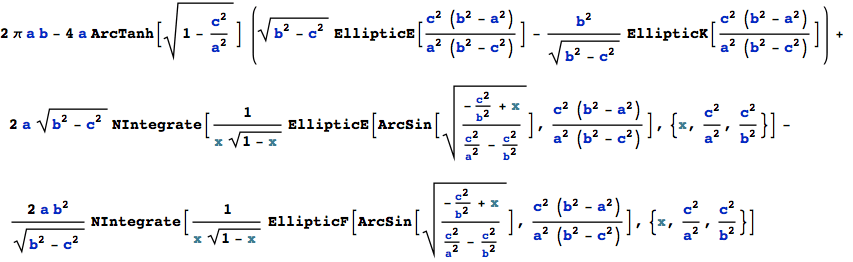
![]()
There are now two integrals left to attack, but luckily, both have already been done – about 130 years ago. The first is:

![]()
![]()
![]()
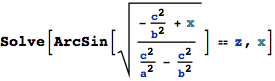
![]()
![]()
![]()
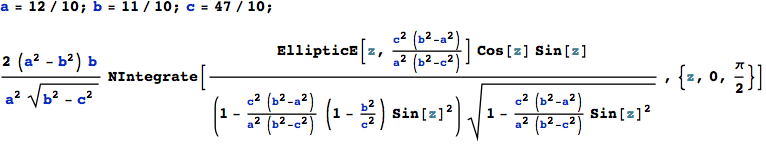
![]()
If the conditions cited at the beginning
• 0 < ( t = ArcCos[b/c] ) < π/2, or equivalently b < c, and
• 0 < k < 1
are all fulfilled, then this integral has a solution, found with Gradshteyn Ryzhik (6.123) (Ref.2) to be :
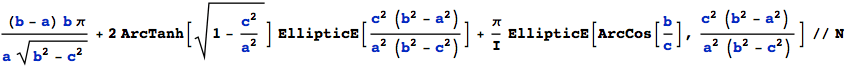
![]()
The second integral is very similar to the first :

![]()
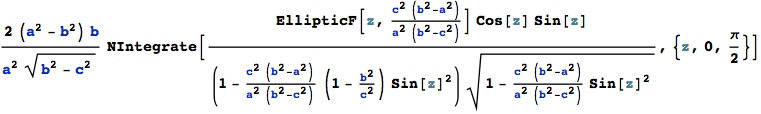
![]()
This is – with Gradshteyn Ryzhik (6.113-2) – :
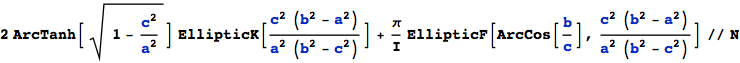
![]()
Put them into the formula for the surface area above :
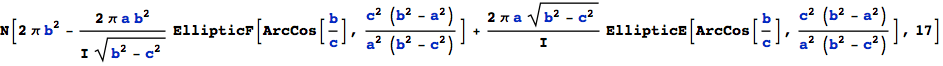
![]()
This is already the correct expression. Now rename the axes, that a > b > c :
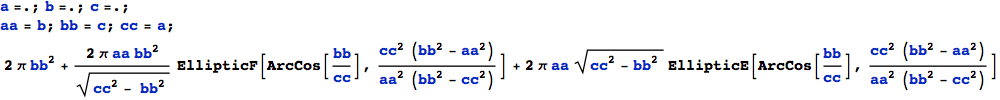
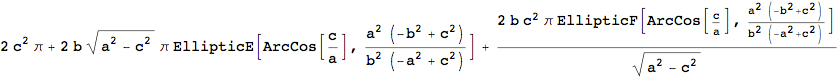
The final result is ( incidentally valid for any set of semi-axes – if a ≠ b ≠ c) :
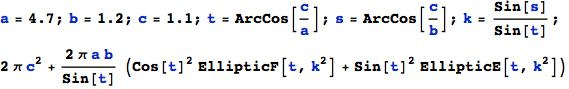
![]()
Prolate case: b→c ; surface of revolution (radius c)
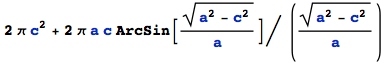
Oblate case: b→a ; surface of revolution (radius a)
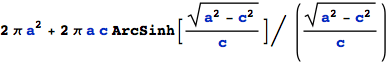
c→a ; surface of sphere
![]()
As a 'pocket calculator' approximation to the surface area of an ellipsoid, that is better than 1.2% (if a > b ≥ c), we may use:
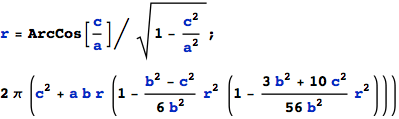
![]()
This formula is shorter and has a smaller more symmetric error than the one given in a previous version of this note (2003).
Note that the first two terms correspond to the prolate surface of revolution.
References
1. Wolfram: The Mathematica Book, Wolfram Media, Inc., Fourth Edition, 1999
2. Gradshteyn/Ryzhik: Table of Integrals, Series and Products, Academic Press, Second Printing, 1981