


Nächste Seite: Freiheitsgrade in Kernmaterie
Aufwärts: Ziele und Arbeitsprogramm
Vorherige Seite: Ziele und Arbeitsprogramm
Präzise Daten für die Nukleonformfaktoren und die Observablen der
sind der Schlüssel für das Verständnis der Nukleonstruktur.
Die Nukleonresonanzen werden charakterisiert durch Anregungsenergie,
Resonanzbreite und den Verlauf der Übergangsformfaktoren
als Funktion des Impulsübertrags. Wichtige Hinweise über die
Struktur sind auch in den Verzweigungsverhältnissen der Zerfälle
enthalten.
Eine systematische Untersuchung wird durch die großen
Resonanzbreiten bei gleichzeitig geringem Abstand der Resonanzenergien
erheblich erschwert. Im Mittelpunkt des Meßprogramms stehen
deshalb zunächst keine ,,flächendeckenden`` Untersuchungen über das
ganze Anregungsspektrum der Nukleonresonanzen, sondern sehr
gezielte Fragestellungen.
Mit Blick auf das Verständnis der Kernkräfte ist das Studium
der niedrigliegenden Resonanzen von besonderem Interesse.
Bei der Anregung der ersten magnetischen Resonanz, 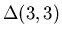 ,
ist nicht die Bestimmung der dominierenden magnetischen
Dipolamplitude das Ziel, sondern die Messung der mehr als eine Größenordnung
kleineren elektrischen Quadrupolamplitude. Diese ist sensitiv auf die Abweichungen
von einer radialsymmetrischen Übergangsladungsverteilung ist.
Solche nicht-radialsymmetrischen Verteilungen sind
eine Signatur nicht-zentralsymmetrischer Kräfte.
sind Kräfte mit einer nicht-trivialen Abhängigkeit von der
Orientierung der Nukleonspins;
das Quadrupolmoment des Deuterons
ist ein schönes Beispiel für die Präsenz von Tensorkräften als Komponente
der Kernkraft.
Nachdem in den letzten Jahren Messungen an ELSA
mit der Reaktion
,
ist nicht die Bestimmung der dominierenden magnetischen
Dipolamplitude das Ziel, sondern die Messung der mehr als eine Größenordnung
kleineren elektrischen Quadrupolamplitude. Diese ist sensitiv auf die Abweichungen
von einer radialsymmetrischen Übergangsladungsverteilung ist.
Solche nicht-radialsymmetrischen Verteilungen sind
eine Signatur nicht-zentralsymmetrischer Kräfte.
sind Kräfte mit einer nicht-trivialen Abhängigkeit von der
Orientierung der Nukleonspins;
das Quadrupolmoment des Deuterons
ist ein schönes Beispiel für die Präsenz von Tensorkräften als Komponente
der Kernkraft.
Nachdem in den letzten Jahren Messungen an ELSA
mit der Reaktion 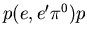 und an MAMI
mit der Reaktion
und an MAMI
mit der Reaktion
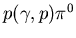 klar etabliert haben,
daß eine Abweichung von einer Radialsymmetrie des N/
klar etabliert haben,
daß eine Abweichung von einer Radialsymmetrie des N/ existiert,
gilt es nun, durch Messung des Quadrupolübergangsformfaktors
die räumliche Verteilung zu bestimmen. Mit einem Flugzeitspektrometer
mit großer Impuls- und Raumwinkelakzeptanz werden die
Rückstoßprotonen der Reaktion
existiert,
gilt es nun, durch Messung des Quadrupolübergangsformfaktors
die räumliche Verteilung zu bestimmen. Mit einem Flugzeitspektrometer
mit großer Impuls- und Raumwinkelakzeptanz werden die
Rückstoßprotonen der Reaktion 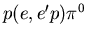 azimutsymmetrisch
um die Richtung der partiell polarisierten virtuellen Photonen
spektroskopiert. Z. Zt. einzigartig wird die Messung derselben Observablen
am im Deuteron gebundenen Proton und Neutron sein. Bindungseffekte könnten
hier den am freien Nukleon gemessenen Wert verändern.
Deswegen wird am Deuteron neben dem Neutron simultan auch das Proton
gemessen, damit dort eine denkbare Änderung festgestellt werden kann.
Es sind auch Messungen
der gleichen Reaktion mit einem polarisierten Elektronenstrahl
vorgesehen. Die Daten einer solchen Messung sind wichtig
zum Verständnis kleinerer, nicht-resonanter Beiträge,
deren Unkenntnis die Größe des systematischen Fehlers bestimmt.
azimutsymmetrisch
um die Richtung der partiell polarisierten virtuellen Photonen
spektroskopiert. Z. Zt. einzigartig wird die Messung derselben Observablen
am im Deuteron gebundenen Proton und Neutron sein. Bindungseffekte könnten
hier den am freien Nukleon gemessenen Wert verändern.
Deswegen wird am Deuteron neben dem Neutron simultan auch das Proton
gemessen, damit dort eine denkbare Änderung festgestellt werden kann.
Es sind auch Messungen
der gleichen Reaktion mit einem polarisierten Elektronenstrahl
vorgesehen. Die Daten einer solchen Messung sind wichtig
zum Verständnis kleinerer, nicht-resonanter Beiträge,
deren Unkenntnis die Größe des systematischen Fehlers bestimmt.
Die Quadrupolamplitude der Photoproduktion wird von jüngsten
Rechnungen [28] gut wiedergegeben.
Resultate von früheren Rechnungen für die
Elektroproduktion stimmen mit dem kleinen, mit relativ großem Fehler
behafteten Datensatz nicht überein.
Die in der Anregungsenergie nächsthöhere Resonanz
nach der  -Resonanz ist die Roper-Resonanz.
Sie hat die gleichen Quantenzahlen wie das Nukleon.
Als
-Resonanz ist die Roper-Resonanz.
Sie hat die gleichen Quantenzahlen wie das Nukleon.
Als
- skalare Anregung des Nukleons
nimmt sie eine
Sonderstellung ein. In Quarkmodellen wird sie als
radiale Anregung der Quarkverteilung beschrieben.
Die niedrige Masse und der Verlauf der elektromagnetischen
Übergangsformfaktoren wird von den meisten Modellrechnungen
nicht richtig wiedergegeben. Es werden deshalb gerade für die
Beschreibung dieser Resonanz immer wieder Modelle vorgeschlagen, die
von anderen Freiheitsgraden ausgehen. So entsteht diese Resonanzanregung
im Rahmen von hadronischen Freiheitsgraden durch eine
resonante Kopplung zwischen Nukleon und Pionwolke [29].
Bei anderen Ansätzen gilt die Roper-Resonanz auch als Evidenz für das
Vorhandensein von expliziten Gluonfreiheitsgraden [30].
Die vorhandenen Daten sind aber nicht genau genug,
um zu entscheiden, ob einem dieser Ansätze der Vorzug zu geben
ist. Messungen der Reaktion
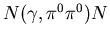 am Neutron und Proton werden ebenso durchgeführt wie
Messungen der Elektroproduktion bei Impulsüberträgen
bis zu
am Neutron und Proton werden ebenso durchgeführt wie
Messungen der Elektroproduktion bei Impulsüberträgen
bis zu 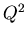 = 0.5
= 0.5 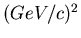 . Besonders interessant, weil
modelldiskriminierend, ist dabei der Verlauf des Übergangsformfaktors
in der Nähe des Photonenpunkts und die Stärke
des longitudinalen/skalaren Anteils. Zur Trennung der
verschiedenen Anteile werden polarisierte Strahlen und
Targets nötig sein.
. Besonders interessant, weil
modelldiskriminierend, ist dabei der Verlauf des Übergangsformfaktors
in der Nähe des Photonenpunkts und die Stärke
des longitudinalen/skalaren Anteils. Zur Trennung der
verschiedenen Anteile werden polarisierte Strahlen und
Targets nötig sein.
Das Anregungsspektrum des Nukleons wurde gut mit der Reaktion
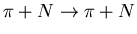 vermessen. Mit dieser Reaktion
wurden auch die meisten der experimentell gesicherten
Resonanzen gefunden. Rechnungen im Rahmen des
nicht-relativistischen Quarkmodells sagen aber ein viel reicheres
Anregungsspektrum von Resonanzen voraus.
Wenn die vorausgesagten Zustände
nicht existieren, ist das ein Hinweis auf weniger interne
Freiheitsgrade. Modelle einer reduzierten Zahl von Baryonen-Resonanzen
sind z. B. Diquarkmodelle, in denen zwei Quarks so stark gebunden sind,
daß Freiheitsgrade wegfallen. Es stellt sich die Frage, ob diese Resonanzen
bisher unentdeckt blieben oder ob sie nicht existieren.
Die Suche nach diesen
muß sich auf andere Zerfallskanäle als den bisher untersuchten (
vermessen. Mit dieser Reaktion
wurden auch die meisten der experimentell gesicherten
Resonanzen gefunden. Rechnungen im Rahmen des
nicht-relativistischen Quarkmodells sagen aber ein viel reicheres
Anregungsspektrum von Resonanzen voraus.
Wenn die vorausgesagten Zustände
nicht existieren, ist das ein Hinweis auf weniger interne
Freiheitsgrade. Modelle einer reduzierten Zahl von Baryonen-Resonanzen
sind z. B. Diquarkmodelle, in denen zwei Quarks so stark gebunden sind,
daß Freiheitsgrade wegfallen. Es stellt sich die Frage, ob diese Resonanzen
bisher unentdeckt blieben oder ob sie nicht existieren.
Die Suche nach diesen
muß sich auf andere Zerfallskanäle als den bisher untersuchten (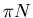 )-Kanal
konzentrieren. Aus theoretischen Überlegungen wird
erwartet, daß zumindest einige Resonanzen sich stark an Zerfallskanäle wie
)-Kanal
konzentrieren. Aus theoretischen Überlegungen wird
erwartet, daß zumindest einige Resonanzen sich stark an Zerfallskanäle wie
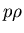 ,
, 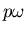 und
und 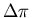 und auch
und auch 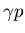 koppeln.
Besonders gut geeignet für die Suche nach fehlenden Resonanzen
ist der (
koppeln.
Besonders gut geeignet für die Suche nach fehlenden Resonanzen
ist der (
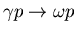 )-Kanal. Mit dem Großraumdetektor
SAPHIR an ELSA kann das
)-Kanal. Mit dem Großraumdetektor
SAPHIR an ELSA kann das
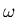 -Meson wegen seiner kleinen Zerfallsbreite gut nachgewiesen werden.
Da das
-Meson wegen seiner kleinen Zerfallsbreite gut nachgewiesen werden.
Da das 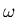 - Meson Isospin I = 0 hat, werden nur Übergänge des
Isospinkanals I = 1/2
selektiert. Diese Selektion eliminiert Beiträge von
- Meson Isospin I = 0 hat, werden nur Übergänge des
Isospinkanals I = 1/2
selektiert. Diese Selektion eliminiert Beiträge von  -Anregungen
und gestattet daher eine gute Identifikation
einer Resonanz. Eine starke Kopplung an den
-Anregungen
und gestattet daher eine gute Identifikation
einer Resonanz. Eine starke Kopplung an den 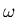 -Kanal
[31] wird z. B. für eine Anregung bei 1.950 GeV
vorausgesagt. Diesen Vorteilen steht auch ein Nachteil
gegenüber; wegen der diffraktiven Konkurrenzprozesse
muß bei relativ hohen Impulsüberträgen gemessen werden - mit entsprechend
kleinen
Wirkungsquerschnitten.
Die Ereignisrate ist aber groß genug, um Resonanzen dieser Art zu finden.
-Kanal
[31] wird z. B. für eine Anregung bei 1.950 GeV
vorausgesagt. Diesen Vorteilen steht auch ein Nachteil
gegenüber; wegen der diffraktiven Konkurrenzprozesse
muß bei relativ hohen Impulsüberträgen gemessen werden - mit entsprechend
kleinen
Wirkungsquerschnitten.
Die Ereignisrate ist aber groß genug, um Resonanzen dieser Art zu finden.
Oberhalb einer Energie von 940 MeV ist es möglich, Hyperonen zu produzieren. Die
Ersetzung z. B. eines
der u-Quarks im Proton durch ein Strange-Quark macht aus dem Proton
ein 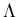 . Die größere Masse und das Einbringen
des Strange-Freiheitsgrades erlaubt erweiterte sensitive Tests
der Baryonmodelle. Neben dem Studium von Resonanzen kann bei höheren Energien
die Dynamik der Quarks unter diesen neuen
Gesichtspunkten berechnet werden.
Durch Beobachtung der Zerfallsteilchen des Hyperons gelingt
auf relativ einfache Weise die Messung der Polarisation der erzeugten
Hyperonen. Mit einem polarisierten Strahl und einem polarisierten
Target wird eine vollständige Bestimmung der Amplituden dieser
Reaktion möglich werden. Darüber hinaus gelingt eine
Isospinzerlegung der Amplituden durch Messungen am
Neutron und am Proton. Mit den Resultaten dieser Messungen
und den begleitenden theoretischen Untersuchungen wird
die Frage nach dem
. Die größere Masse und das Einbringen
des Strange-Freiheitsgrades erlaubt erweiterte sensitive Tests
der Baryonmodelle. Neben dem Studium von Resonanzen kann bei höheren Energien
die Dynamik der Quarks unter diesen neuen
Gesichtspunkten berechnet werden.
Durch Beobachtung der Zerfallsteilchen des Hyperons gelingt
auf relativ einfache Weise die Messung der Polarisation der erzeugten
Hyperonen. Mit einem polarisierten Strahl und einem polarisierten
Target wird eine vollständige Bestimmung der Amplituden dieser
Reaktion möglich werden. Darüber hinaus gelingt eine
Isospinzerlegung der Amplituden durch Messungen am
Neutron und am Proton. Mit den Resultaten dieser Messungen
und den begleitenden theoretischen Untersuchungen wird
die Frage nach dem
- ,,Inhalt an Seltsamkeit`` in der Wellenfunktion des Nukleons
in einem neuen Licht erscheinen.
Der eventuelle Beitrag von Seltsamkeit in der Wellenfunktion
des Nukleons wird bei einer gänzlich anderen Fragestellung
zur Nukleonstruktur wiederum aktuell, nämlich bei der
Frage nach der Spinstruktur des Nukleons. Für die frühe Akzeptanz
des Quarkmodells war die fast quantitative Beschreibung des
Verhältnisses der magnetischen Momente von Proton und Neutron wichtig.
Weitere Daten von magnetischen Momenten z. B. von Hyperonen
stützten die Aussagen der Quarkmodelle bezüglich des Spins.
Es war deshalb eine Überaschung, als Messungen von der
EMC-Kollaboration mit einem hochenergetischen Muonstrahl
das frühere Bild erschütterten, nach dem sich der Spin des Nukleons
aus dem Spin der u- und d-Quarks zusammensetzt.
Nach heutigem Wissen tragen die u- und d-Quarks
mit ihren Spins zu weniger als 50 Prozent zum Gesamtspin
des Nukleons bei. Für den Rest sind Beiträge der
Strange-Quarks und auf die chirale Struktur des QCD-Vakuums zurückzuführende
Anomalien verantwortlich.
Wie im Bereich von hohen Impulsüberträgen
gibt es auch bei niedrigen Energien auf den Eckpfeilern der Theorie
basierende Summenregeln. Die GDH-Summenregel verknüpft den Wert
des magnetischen Moments des Nukleons, also einer statischen Größe,
mit dem Integral über die Energie für den totalen
Absorptionswirkungsquerschnitt von zirkular polarisierten reellen Photonen.
Die Integration muß über einen großen Energiebereich (bis 3 GeV)
durchgeführt werden. Dies ist nur in enger Zusammenarbeit der
beiden Labors in Bonn und Mainz möglich.
Messungen des totalen Wirkungsquerschnitts für zirkular polarisierte
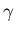 -Quanten
sollen daher sowohl an MAMI für niedrige als auch an ELSA
für hohe Energien durchgeführt werden. Zum Test von Modellen ist auch
eine Überprüfung der Abhängigkeit des GDH-Integrals als
Funktion des Impulsübertrags wichtig. Mit der inklusiven Reaktion
-Quanten
sollen daher sowohl an MAMI für niedrige als auch an ELSA
für hohe Energien durchgeführt werden. Zum Test von Modellen ist auch
eine Überprüfung der Abhängigkeit des GDH-Integrals als
Funktion des Impulsübertrags wichtig. Mit der inklusiven Reaktion
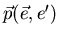 wird diese Reaktion am ELAN-Meßplatz untersucht.
Das vorhandene Magnetspektrometer ist, wegen seiner großen
Impulsakzeptanz, zum Nachweis der gestreuten Elektronen
hervorragend geeignet.
Der nächste Schritt,
wird diese Reaktion am ELAN-Meßplatz untersucht.
Das vorhandene Magnetspektrometer ist, wegen seiner großen
Impulsakzeptanz, zum Nachweis der gestreuten Elektronen
hervorragend geeignet.
Der nächste Schritt,
- die Spinstruktur des Nukleons
zu explorieren, wird mit exklusiven Prozessen der Einfachphotopionproduktion
am Nukleon bei Energien über dem Resonanzbereich angegangen.
Daten vom DESY deuten daraufhin, daß ab Impulsüberträgen
von t = -0.5 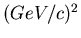 die Produktion der Pionen von der
Absorption der Photonen an Quarks bestimmt wird. Experimente
mit polarisierten Photonen an einem polarisierten Target werden diese
Hypothese überprüfen können. Das Experiment wird aus Intensitätsgründen
an einem Bremsstrahl am ELAN - Meßplatz vorgesehen.
die Produktion der Pionen von der
Absorption der Photonen an Quarks bestimmt wird. Experimente
mit polarisierten Photonen an einem polarisierten Target werden diese
Hypothese überprüfen können. Das Experiment wird aus Intensitätsgründen
an einem Bremsstrahl am ELAN - Meßplatz vorgesehen.
Bei niedrigen Energien in der Nähe des statischen Grenzfalls
kann das Nukleon als punktförmiges Dirac-Teilchen mit einer
Wolke von Goldstone-Bosonen betrachtet werden.
Die relevanten Freiheitsgrade sind hadronischer Natur.
Mit der chiralen Störungstheorie (CHPT) existiert ein Rahmen, der
es gestattet, alle Reaktionen mit 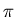 -Mesonen
bei niedrigen Energien miteinander in Beziehung zu setzen. Präzise
Messungen der Photo- und Elektroproduktion von
-Mesonen
bei niedrigen Energien miteinander in Beziehung zu setzen. Präzise
Messungen der Photo- und Elektroproduktion von 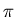 -Mesonen
erlauben deshalb aussagekräftige
-Mesonen
erlauben deshalb aussagekräftige
- Tests der gebrochenen chiralen Symmetrie der QCD
im Sektor der Baryonen. Zu den Goldstone-Bosonen gehören aber auch die
K- und  -Mesonen; eine besondere Rolle spielt zusätzlich das
-Mesonen; eine besondere Rolle spielt zusätzlich das  '-Meson
wegen seiner starken Mischung mit dem
'-Meson
wegen seiner starken Mischung mit dem  -Meson.
Zur Beschreibung derartiger Reaktionen ist sicherlich noch ein langer
Weg zurückzulegen. Um diese Mesonen in den Rahmen der Theorie
aufzunehmen, muß die CHPT um den Freiheitsgrad, den das Strange-Quark
einbringt, erweitert werden. Wegen der großen Strange-Quarkmasse
sind die Schleifenkorrekturen groß, und Rechnungen
müssen höhere Ordnungen berücksichtigen, als dies für den Fall
von u- und d-Quarks nötig ist.
Präzise Daten für die Photo- und Elektroproduktion von
K-,
-Meson.
Zur Beschreibung derartiger Reaktionen ist sicherlich noch ein langer
Weg zurückzulegen. Um diese Mesonen in den Rahmen der Theorie
aufzunehmen, muß die CHPT um den Freiheitsgrad, den das Strange-Quark
einbringt, erweitert werden. Wegen der großen Strange-Quarkmasse
sind die Schleifenkorrekturen groß, und Rechnungen
müssen höhere Ordnungen berücksichtigen, als dies für den Fall
von u- und d-Quarks nötig ist.
Präzise Daten für die Photo- und Elektroproduktion von
K-,  - und
- und  '-Mesonen könnten - wie schon bei der Pionproduktion -
die Initialzündung für
theoretische Untersuchungen für den Strange-Sektor der CHPT geben.
Die Wirkungsquerschnitte in Schwellennähe sind klein, können aber
im Falle der Photoproduktion am Proton mit den Reaktionen
p(
'-Mesonen könnten - wie schon bei der Pionproduktion -
die Initialzündung für
theoretische Untersuchungen für den Strange-Sektor der CHPT geben.
Die Wirkungsquerschnitte in Schwellennähe sind klein, können aber
im Falle der Photoproduktion am Proton mit den Reaktionen
p(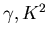 )
)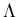 p(
p(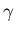 ,p)
,p) /
/ '
untersucht werden. Sehr nahe der Erzeugungsschwelle, also dem hier
interessierenden Gebiet, werden alle Protonen in einen engen Kegel emittiert
und können mit dem an ELAN existierenden Magnetspektrometer
analysiert werden. Auch hier ist wegen der kleinen Produktionsquerschnitte
die Nutzung des Bremsstrahls angebracht.
'
untersucht werden. Sehr nahe der Erzeugungsschwelle, also dem hier
interessierenden Gebiet, werden alle Protonen in einen engen Kegel emittiert
und können mit dem an ELAN existierenden Magnetspektrometer
analysiert werden. Auch hier ist wegen der kleinen Produktionsquerschnitte
die Nutzung des Bremsstrahls angebracht.



Nächste Seite: Freiheitsgrade in Kernmaterie
Aufwärts: Ziele und Arbeitsprogramm
Vorherige Seite: Ziele und Arbeitsprogramm
Frank Frommberger
2000-02-07