Table of Integrals

A. Dieckmann, Physikalisches Institut der Uni Bonn

This integral table contains hundreds of expressions: indefinite and definite integrals of elliptic integrals, of square roots, arcustangents and a few more exotic functions. Most of them are not found in Gradshteyn-Ryzhik.

Sometimes m, n, k denote real parameters and are restricted mostly to 0 < {m, n, k} < 1, at times they represent natural numbers.

Results may be valid outside of the given region of parameters, but should always be checked numerically!

Integrals kindly contributed by Mariusz Iwaniuk are appended at the bottom of this page.

Definite Integrals:

Substitute      and the Feynman-Hibbs Integral can be calculated with Mathematica:

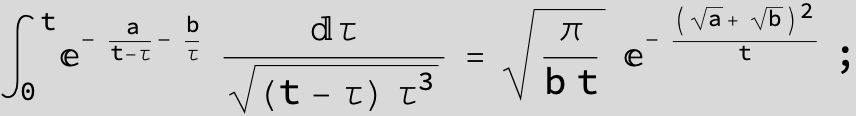
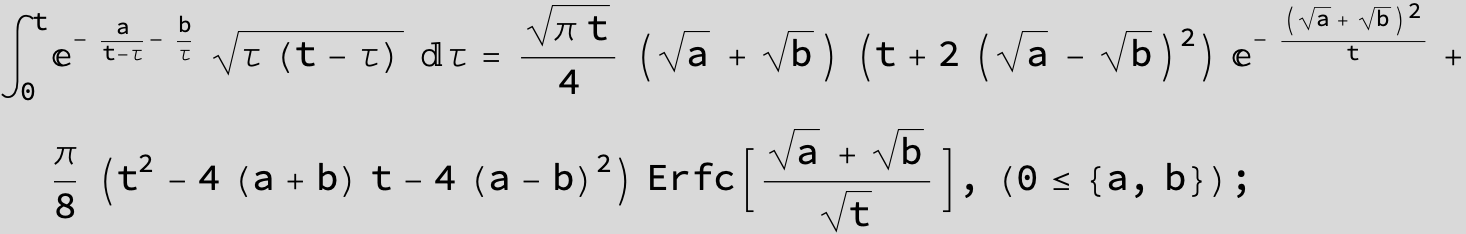
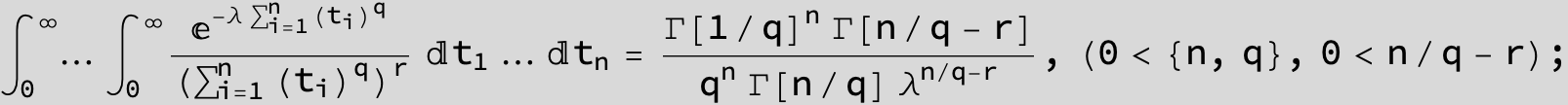
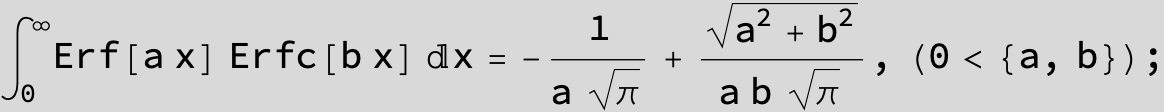
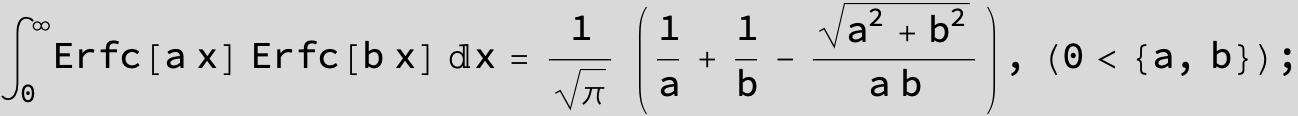
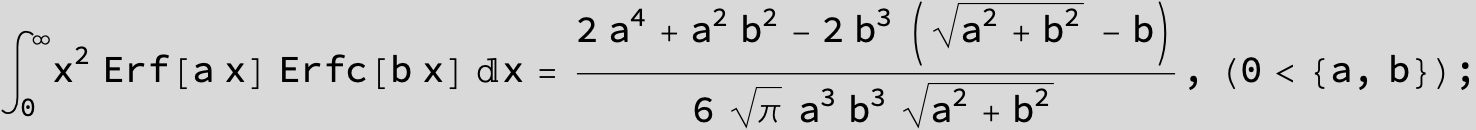
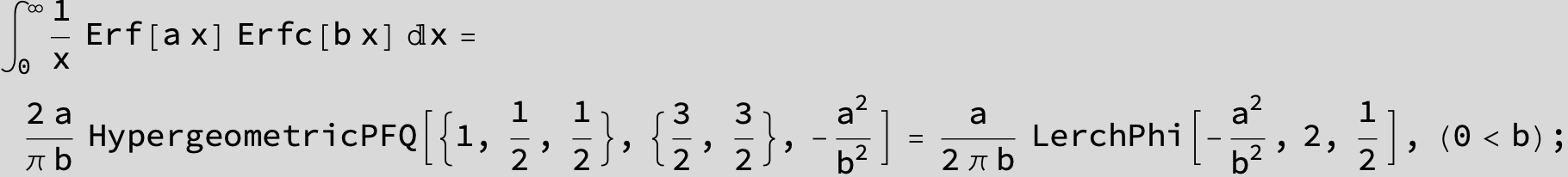
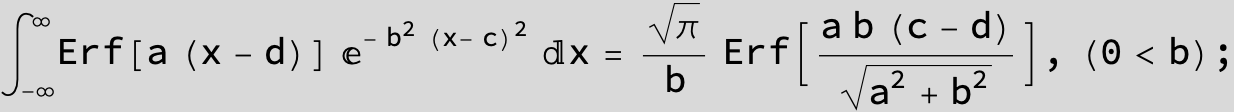
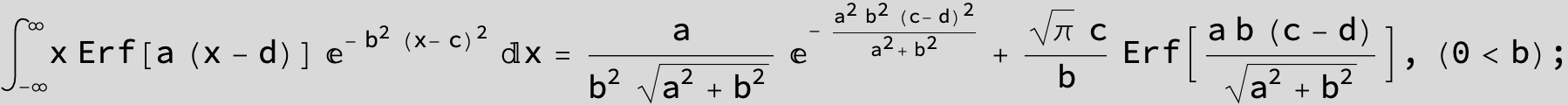
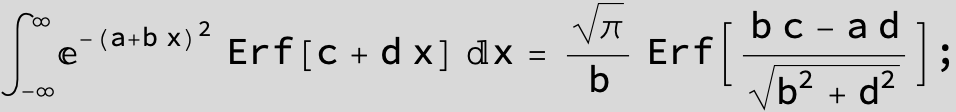
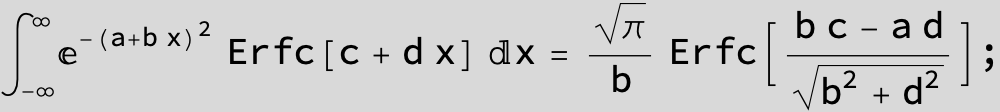
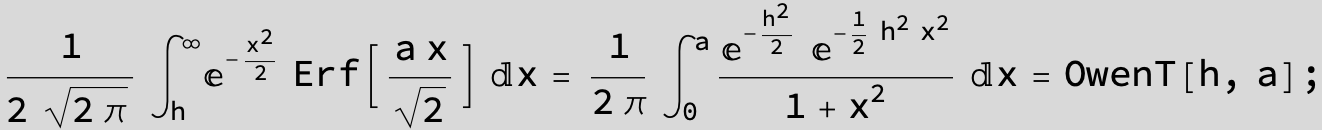
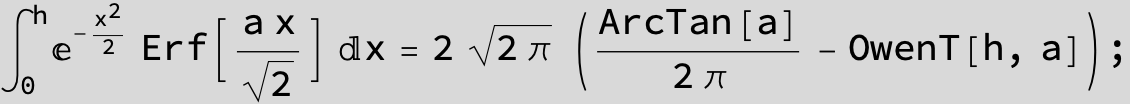
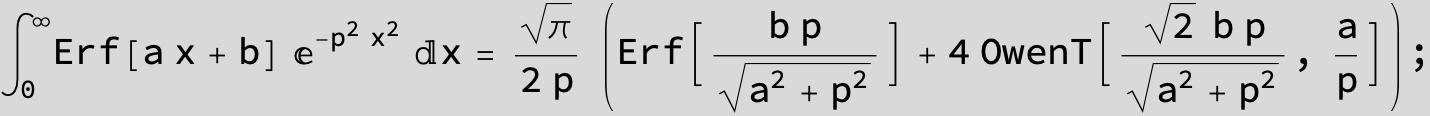
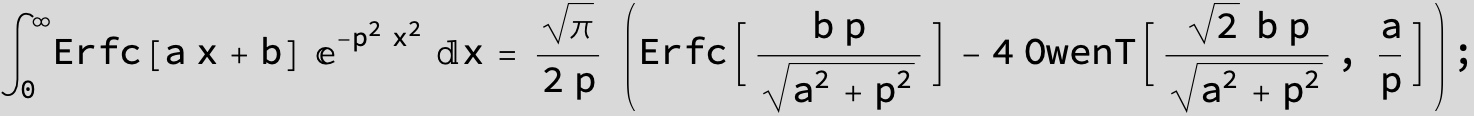
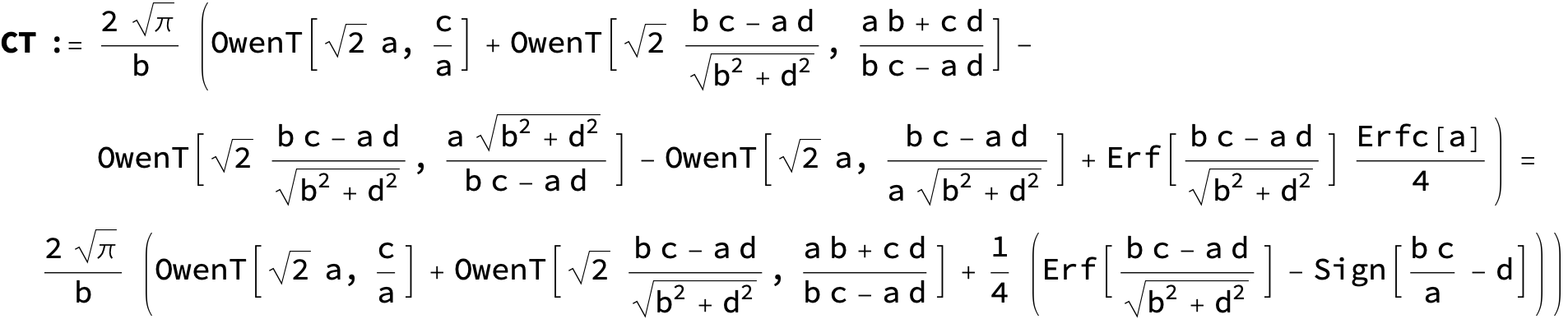
The expression below containing OwenT functions shows up as Common  Term

in the next six integrals combining Gauss- and Error functions with general linear arguments and integration range from Zero to Infinity :

(The integral above got cracked on my daughter' s birthday, so I call it Charlotte' s Integral .)

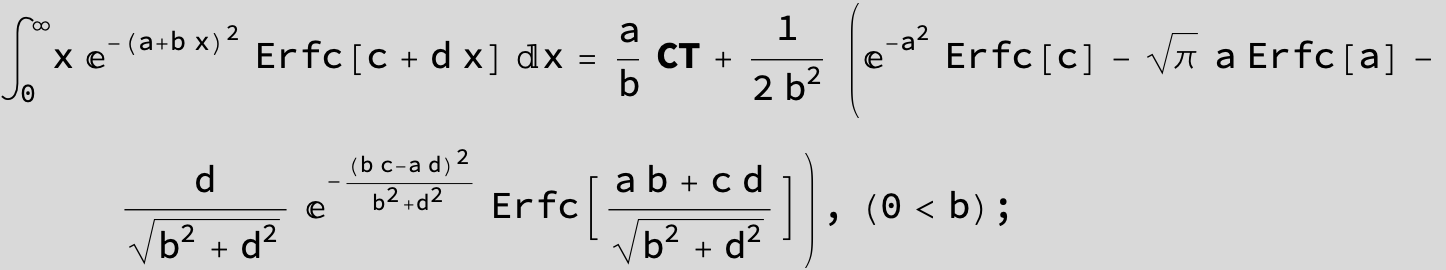
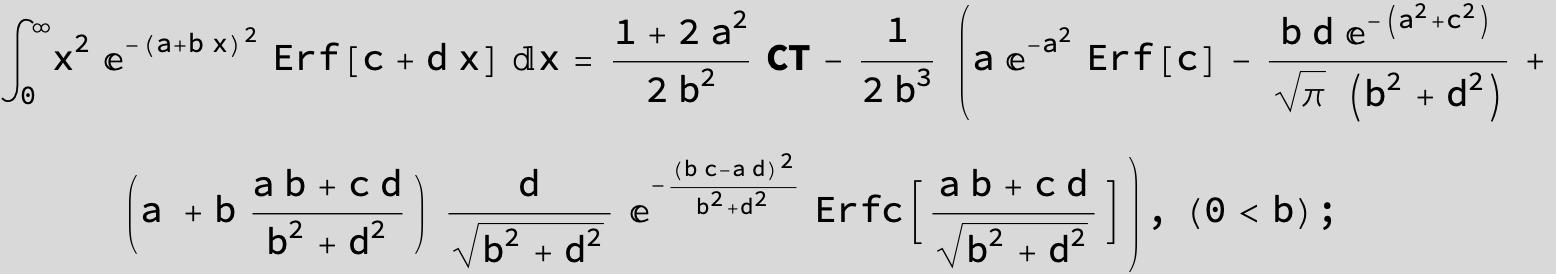
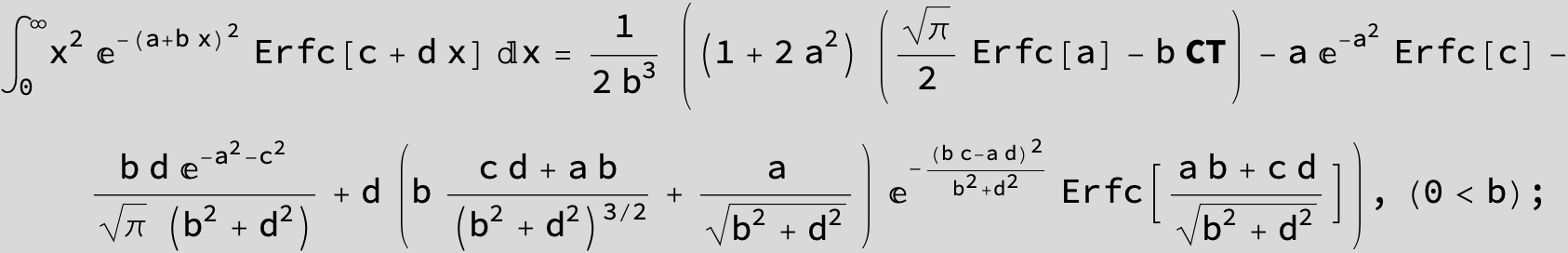
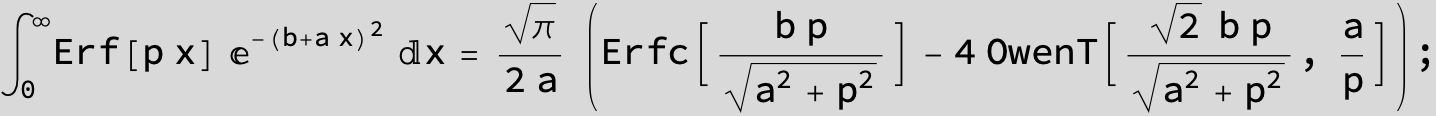
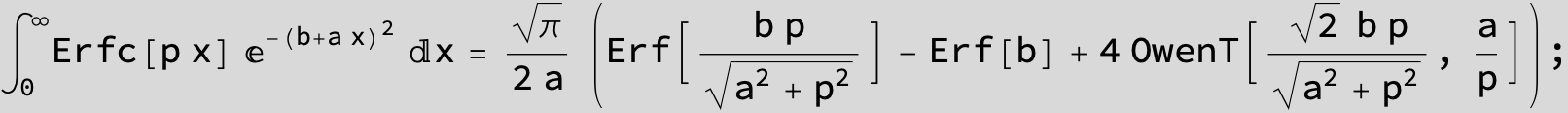
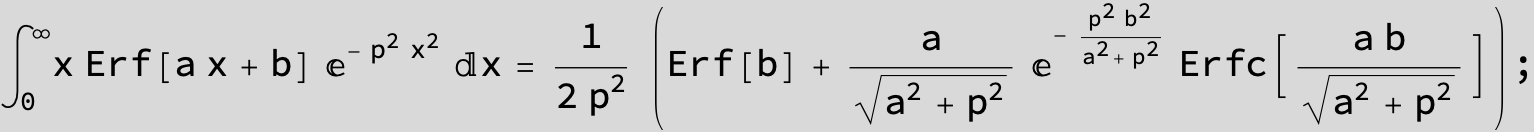
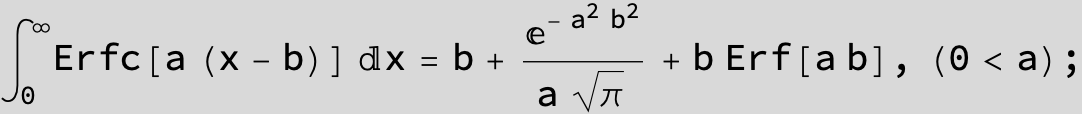
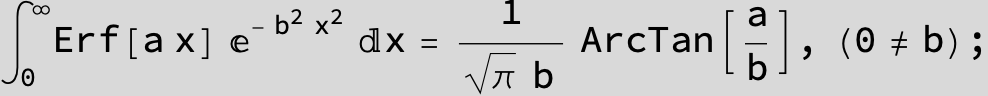
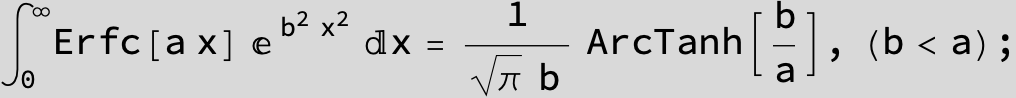
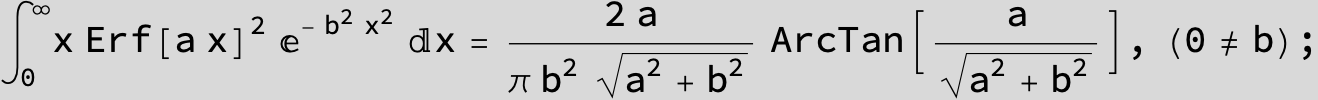
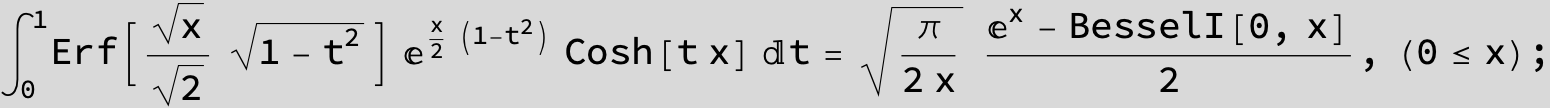
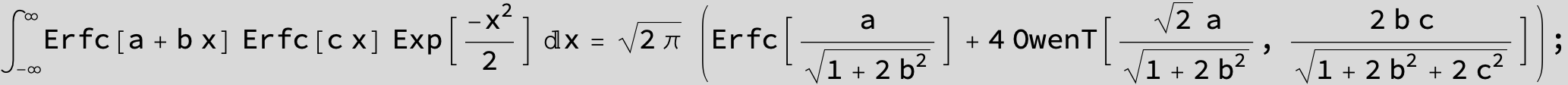
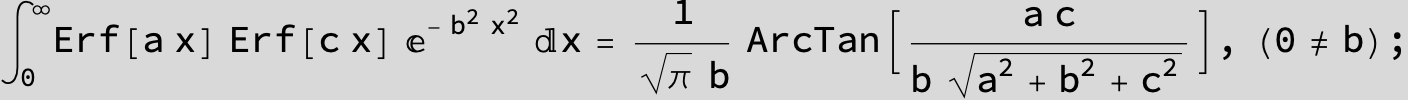
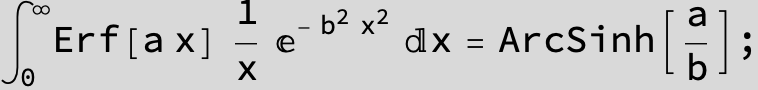
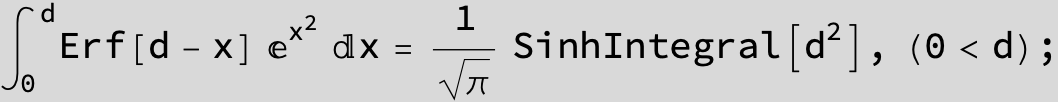
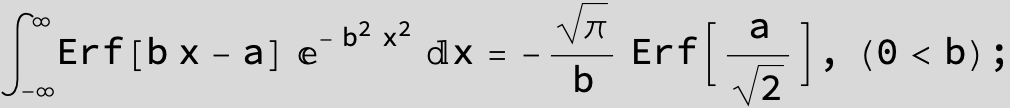
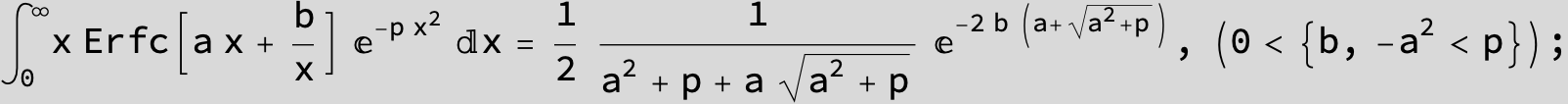
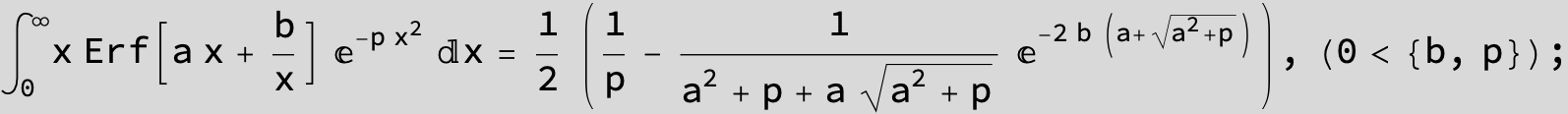
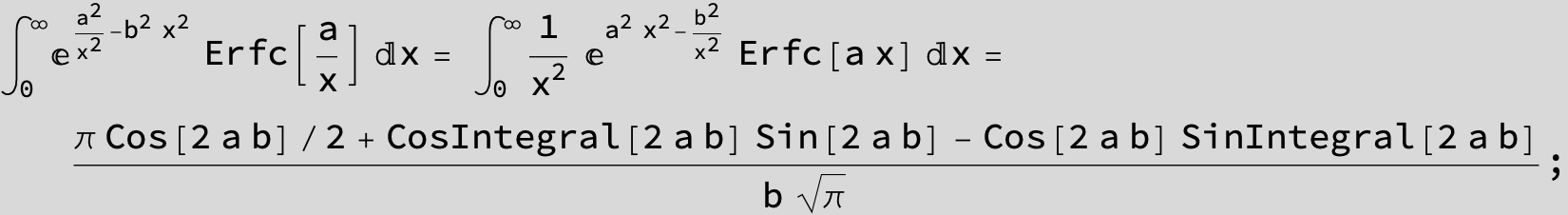
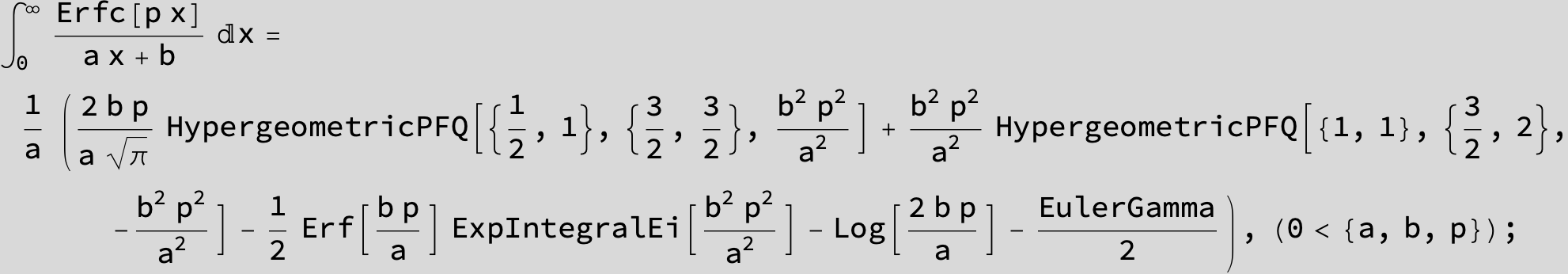
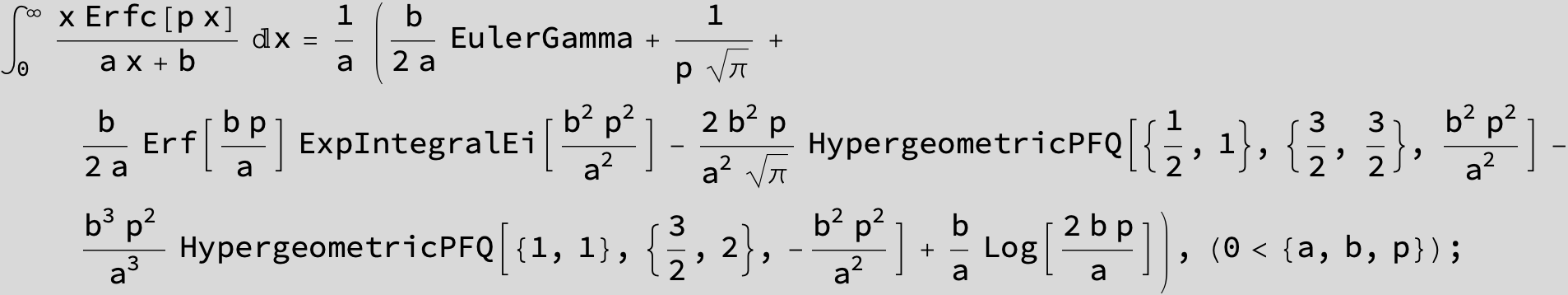
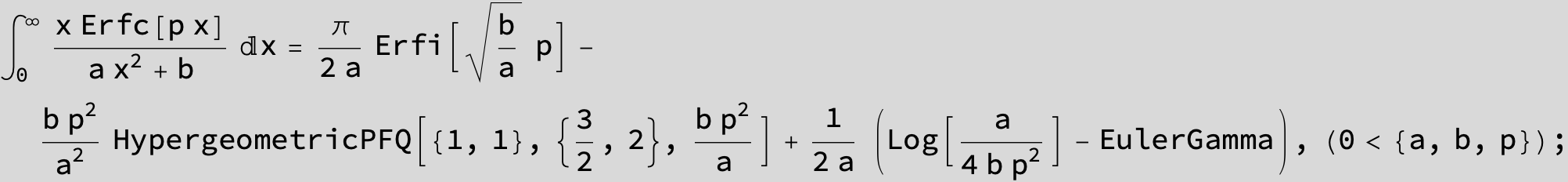
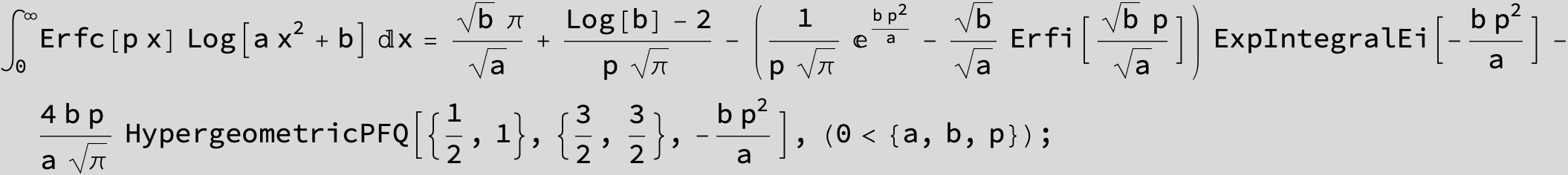
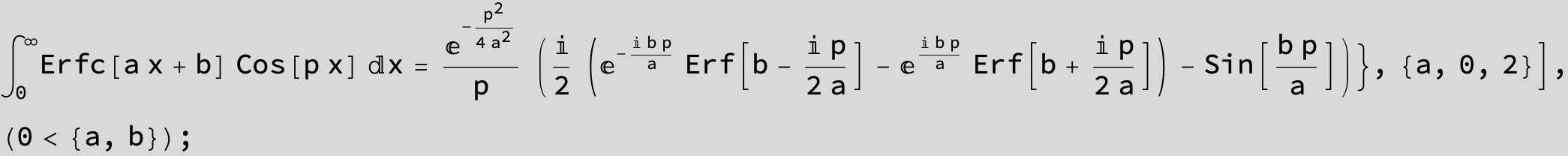
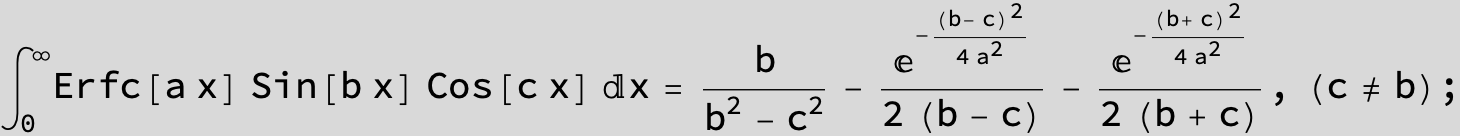
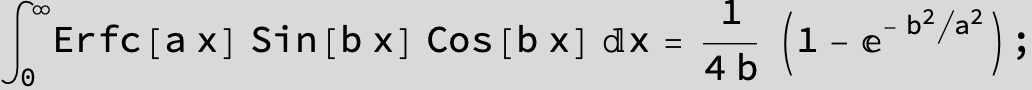
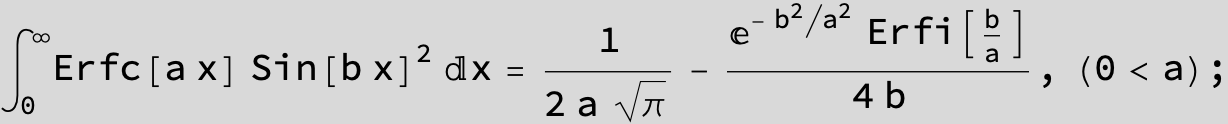
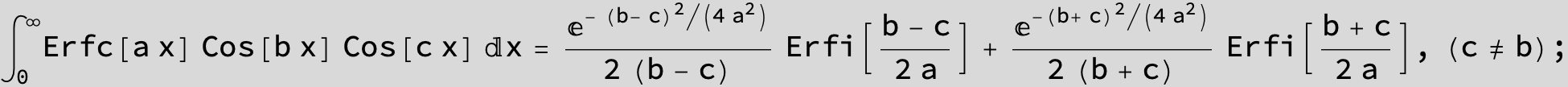
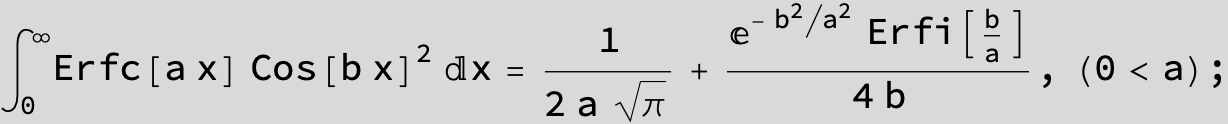
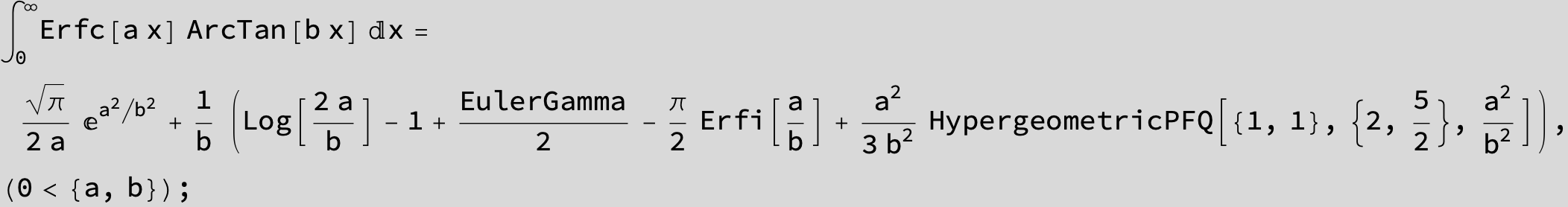
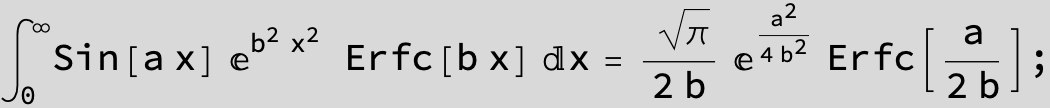
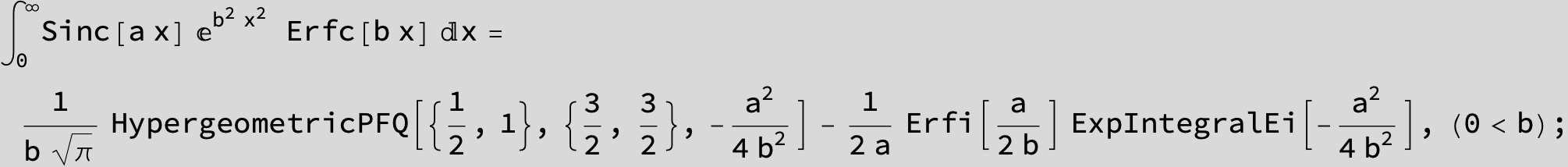
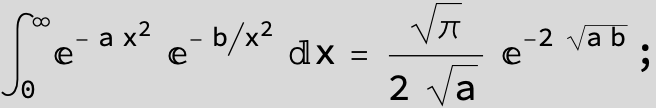
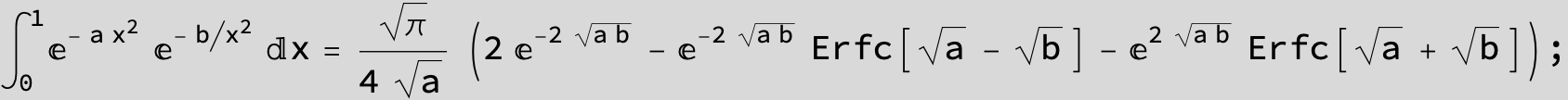
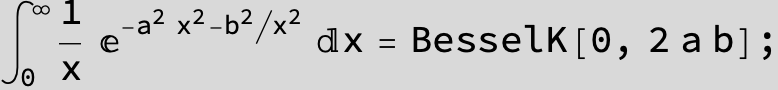
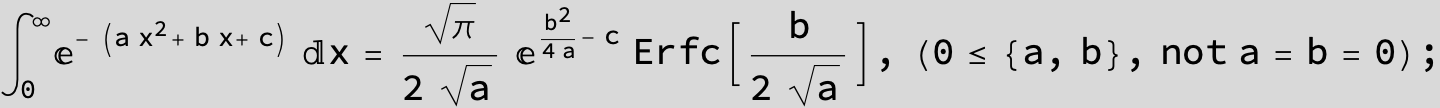
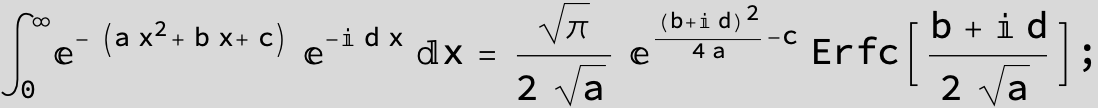
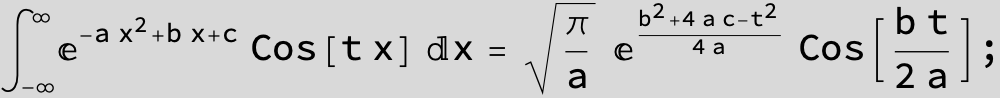
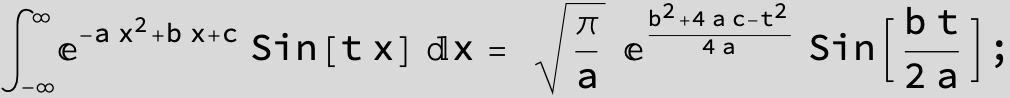
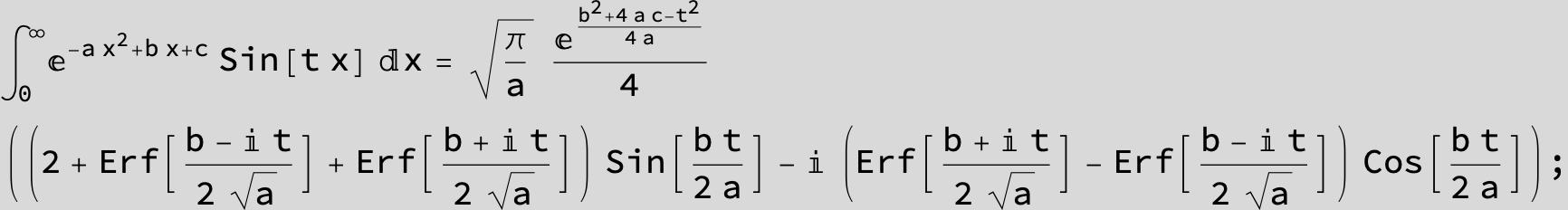
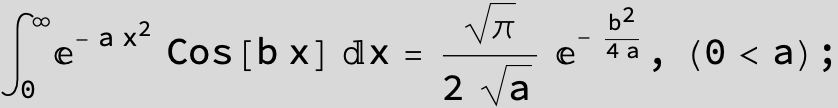
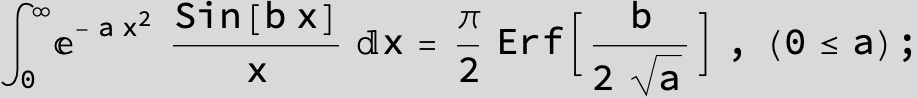
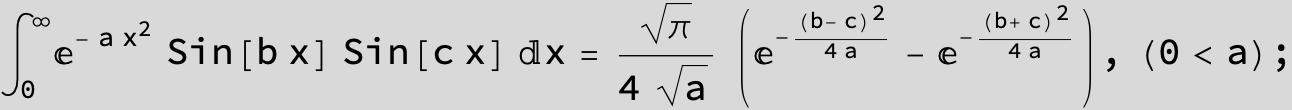
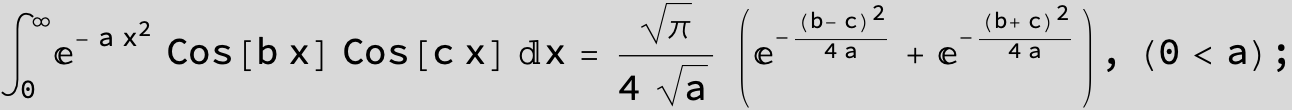
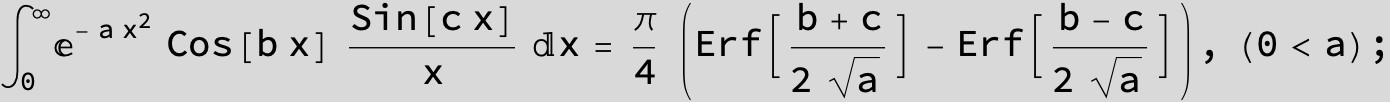
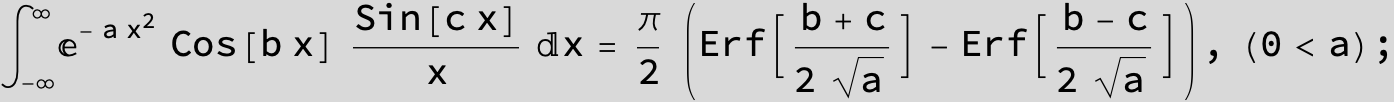
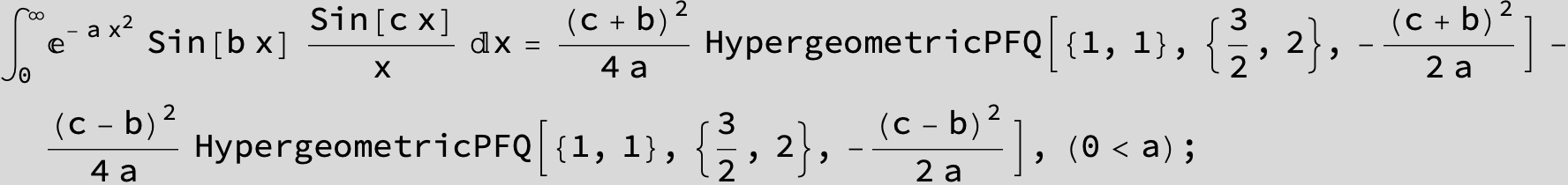
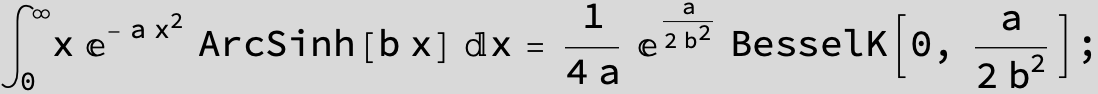
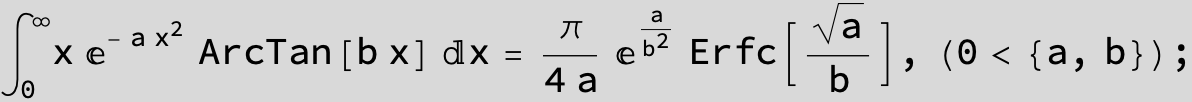
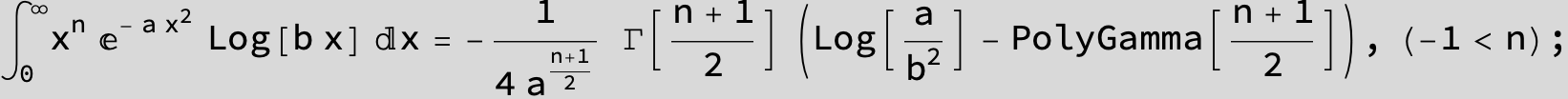
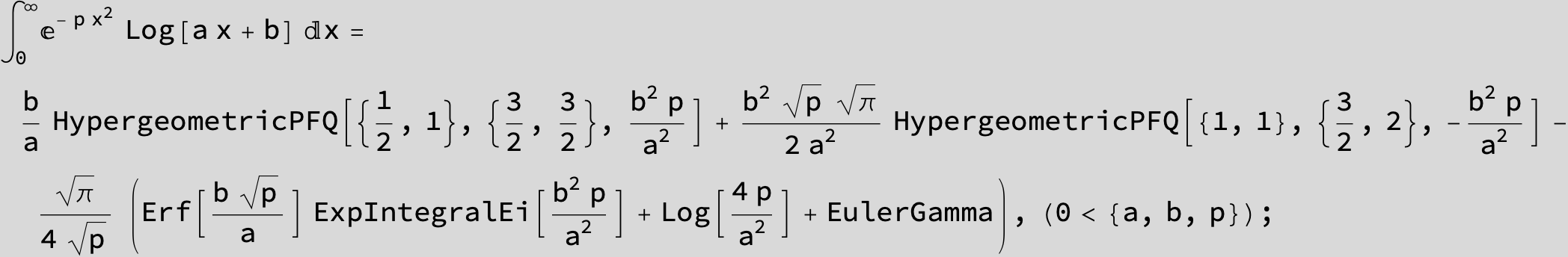
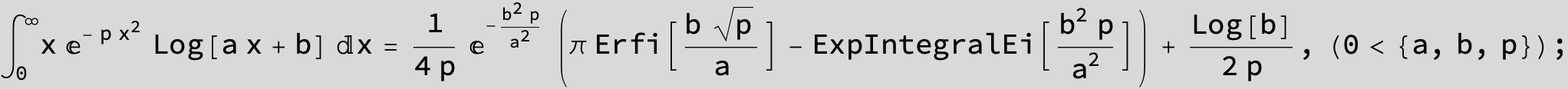
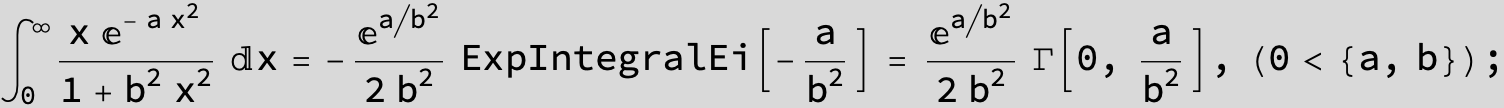
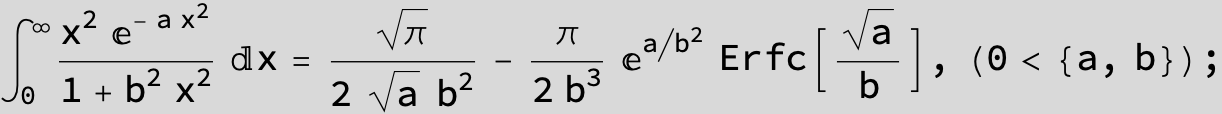
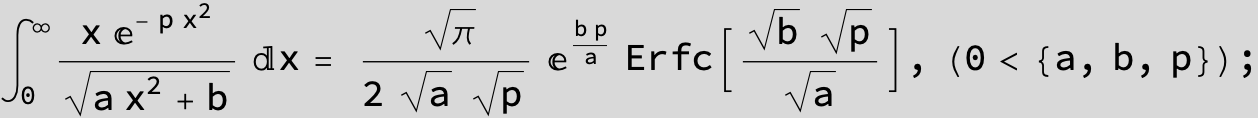
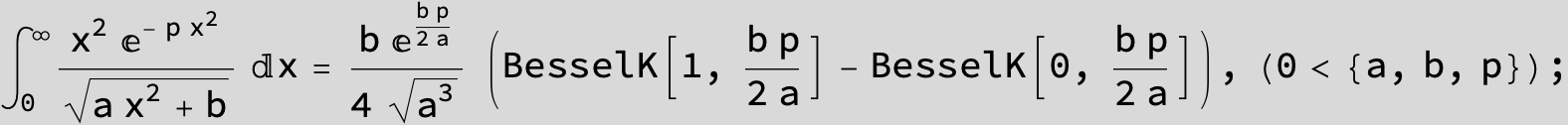
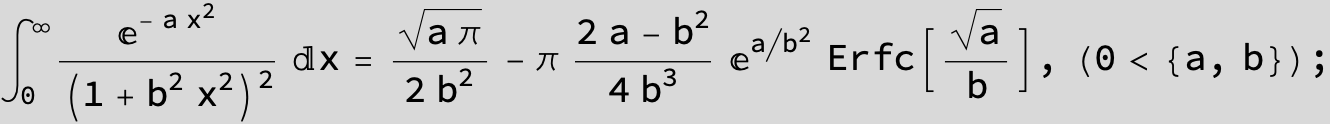
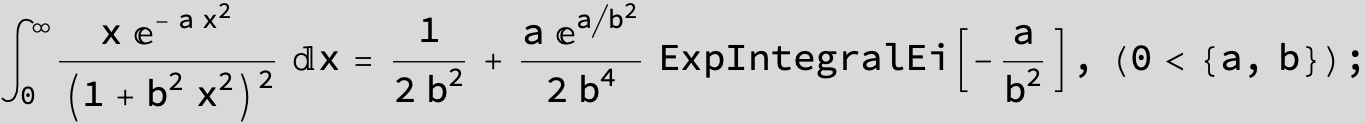
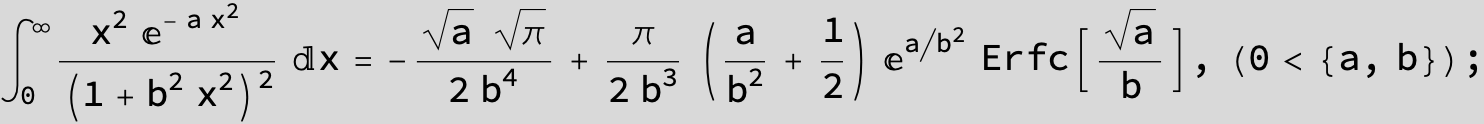
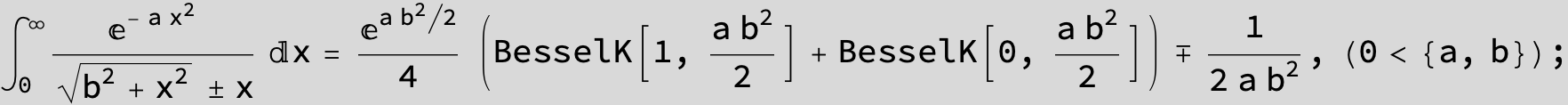
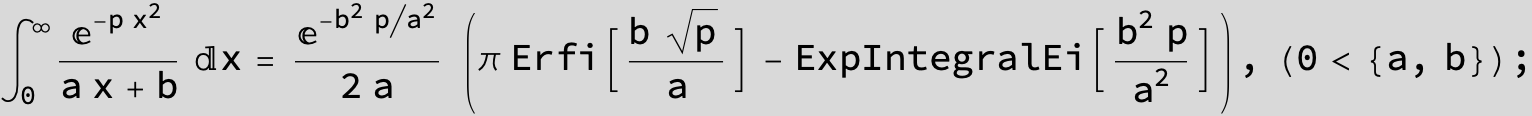
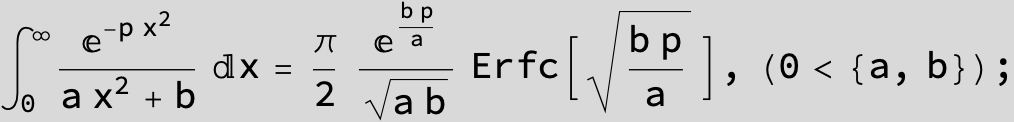
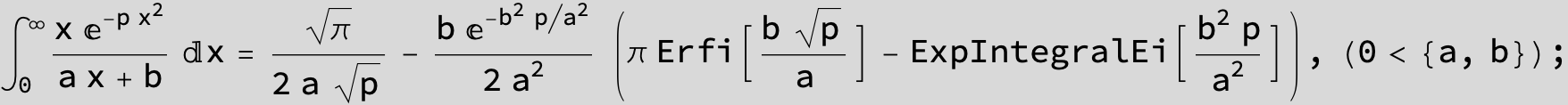
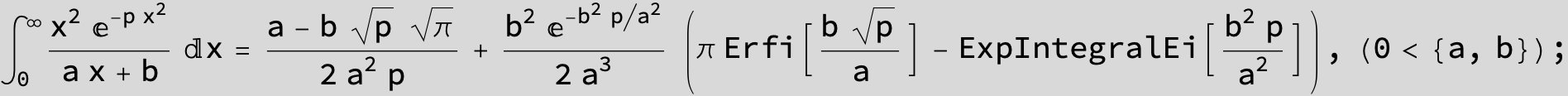
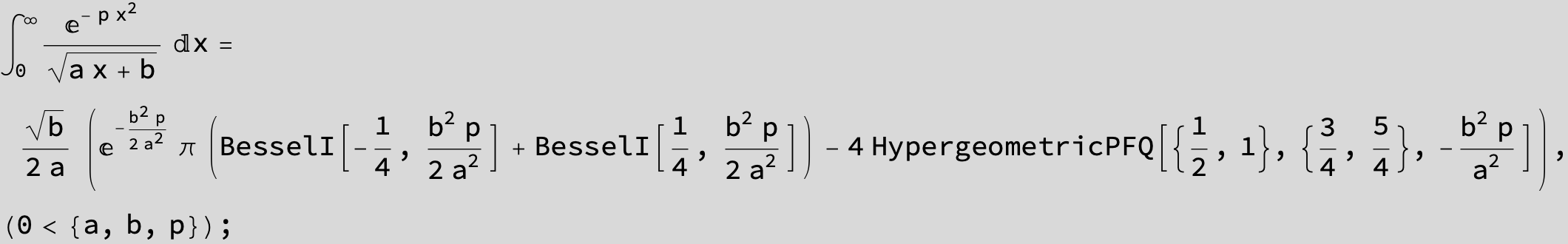
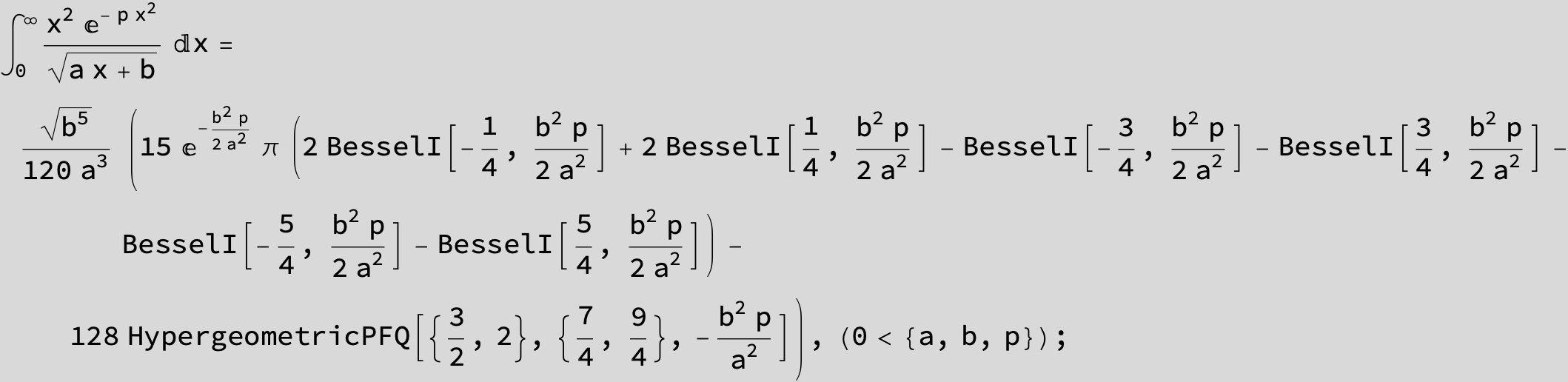
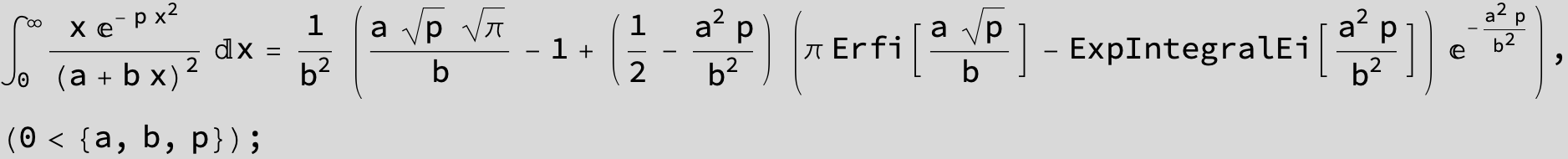
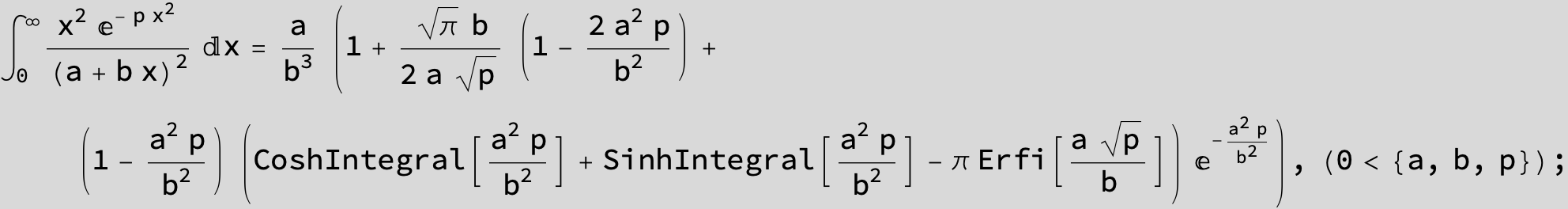
To see a nice cancellation of singularities at work plot the next expression around c = negative Integer:

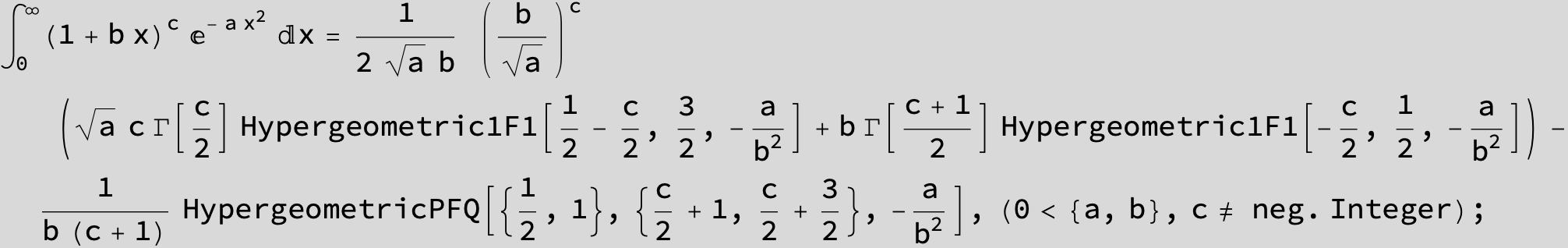
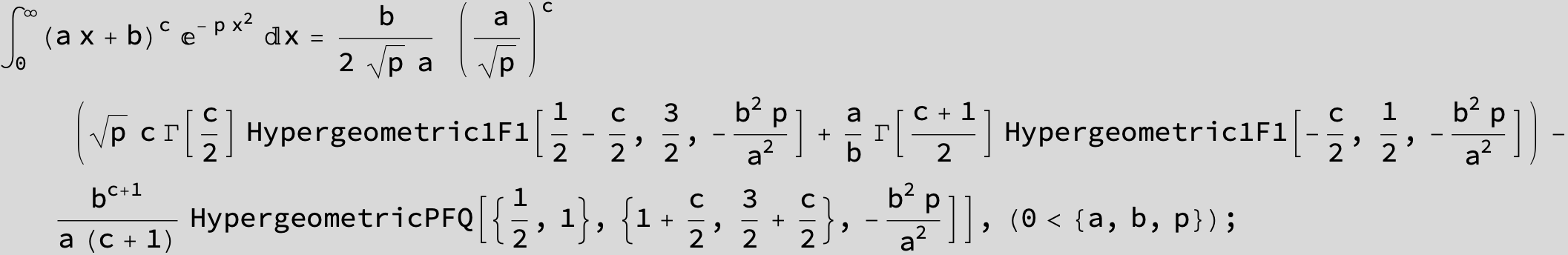
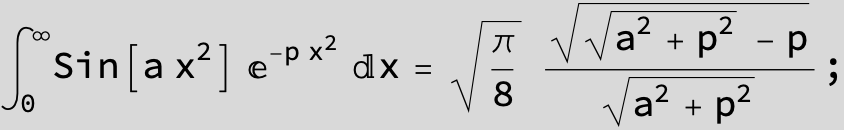
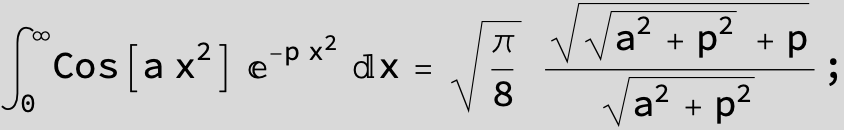
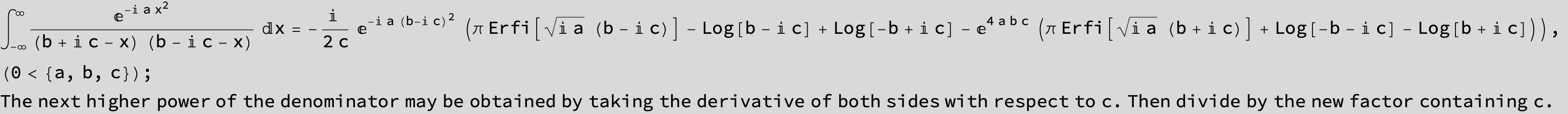
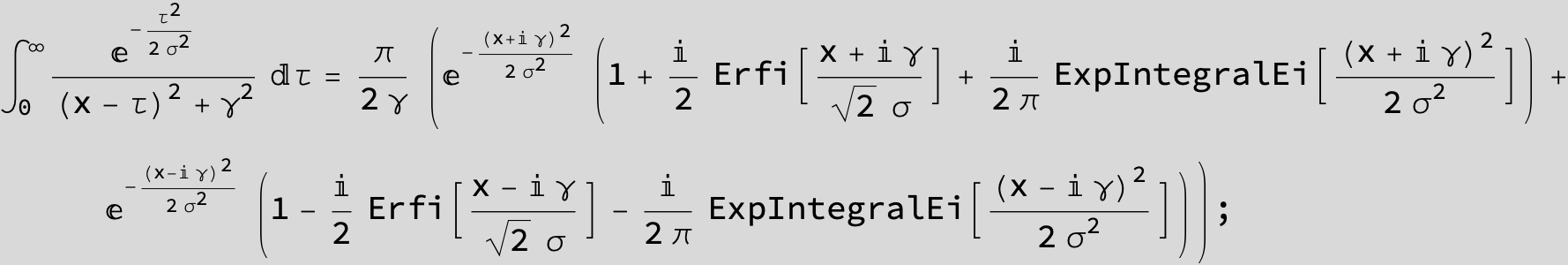
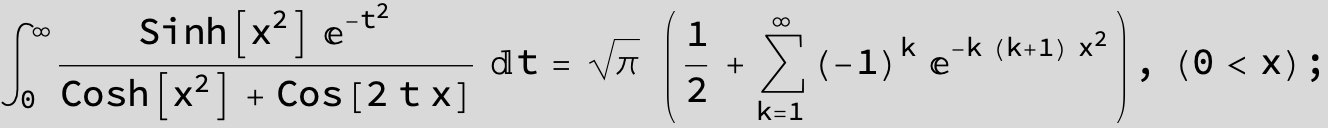
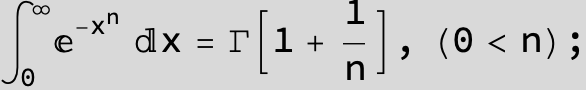
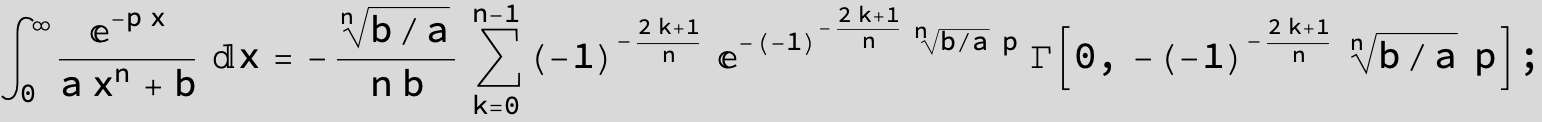
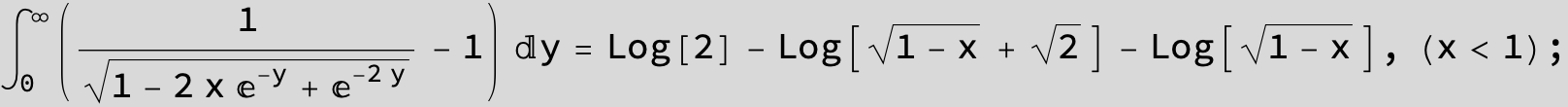
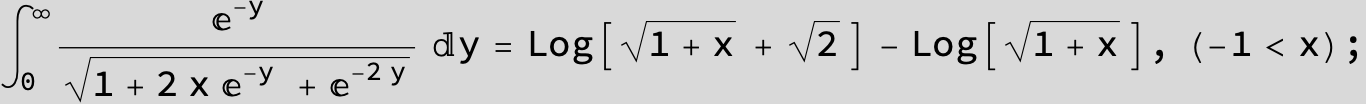
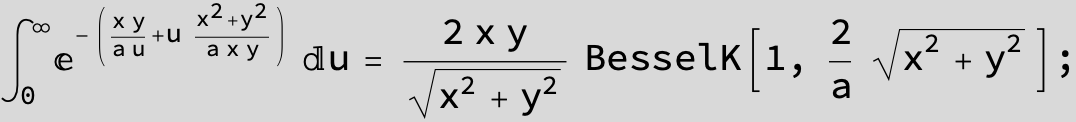
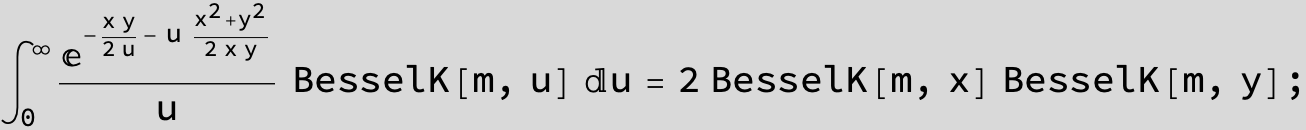
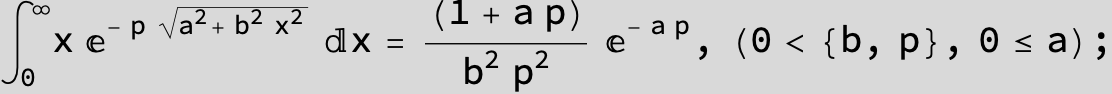
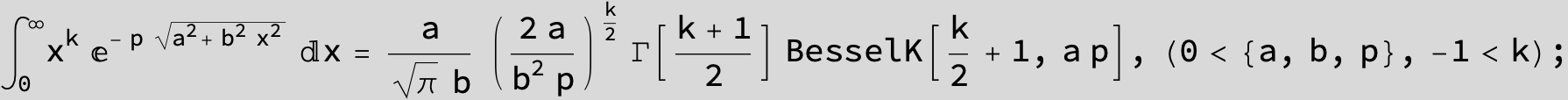
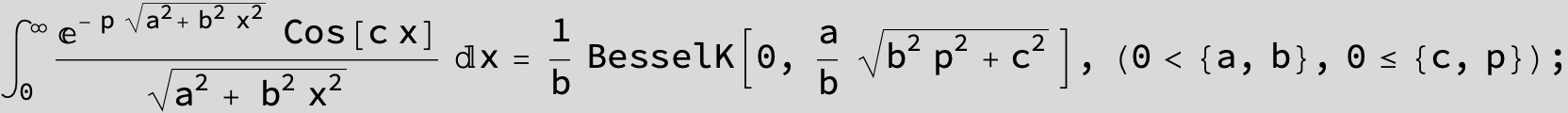
…this is a special case of the next integral below (m = -1 / 2).

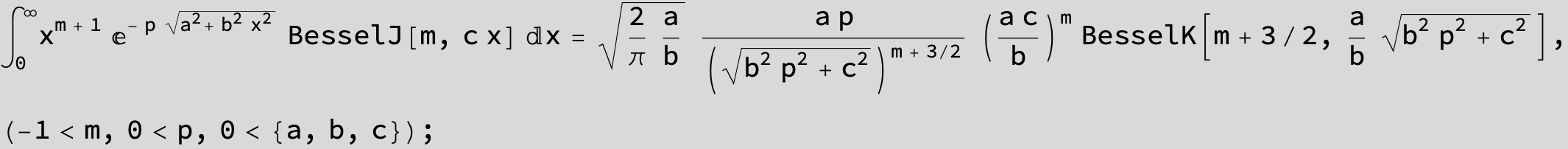
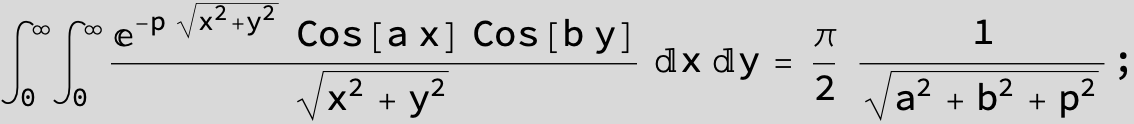
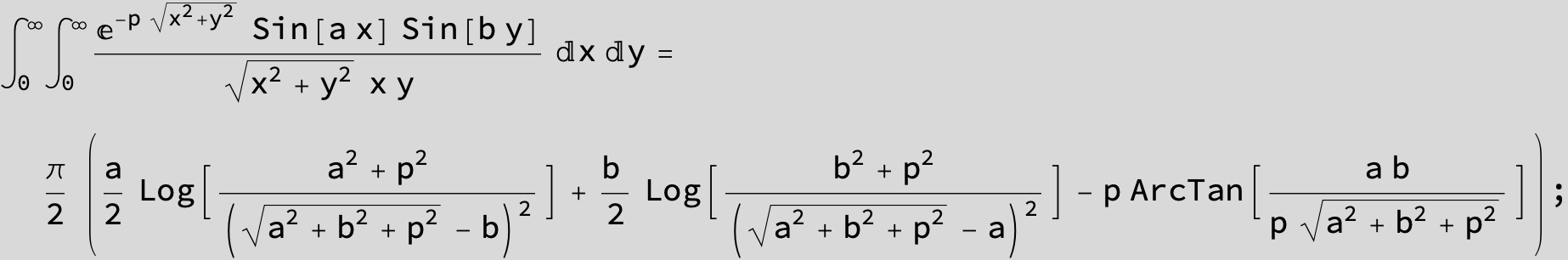
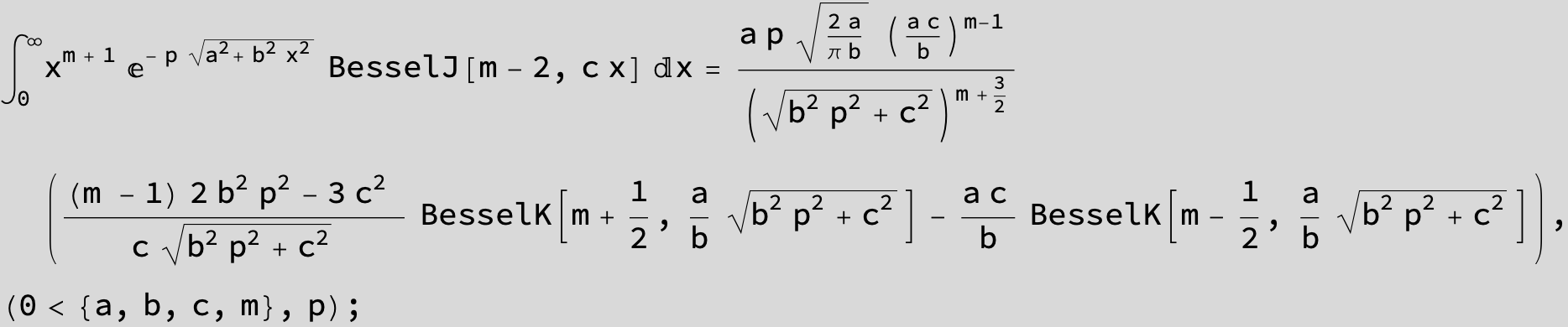
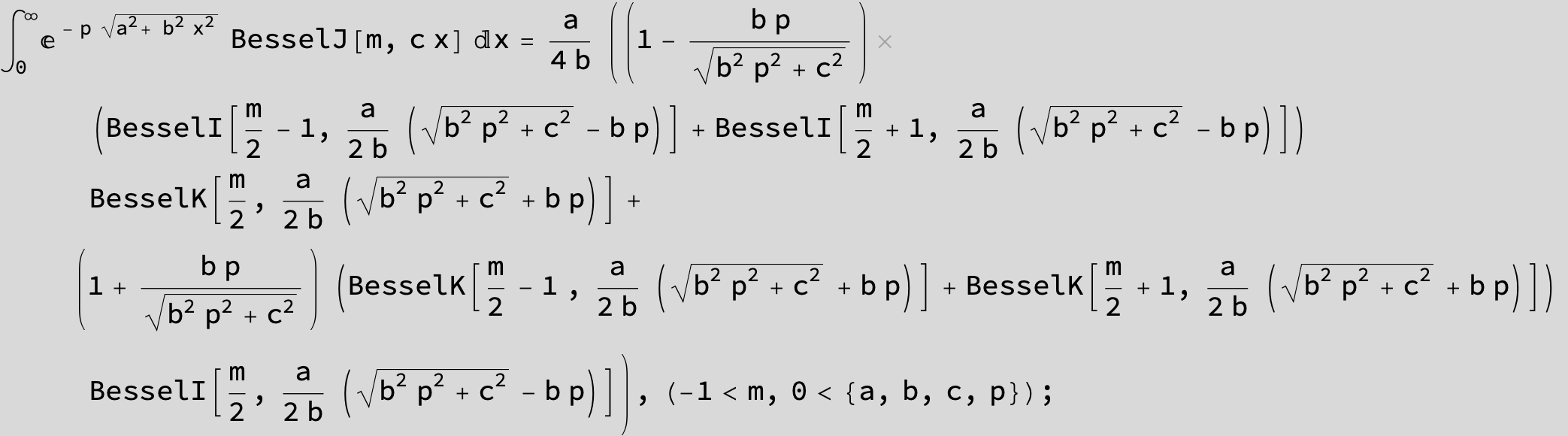
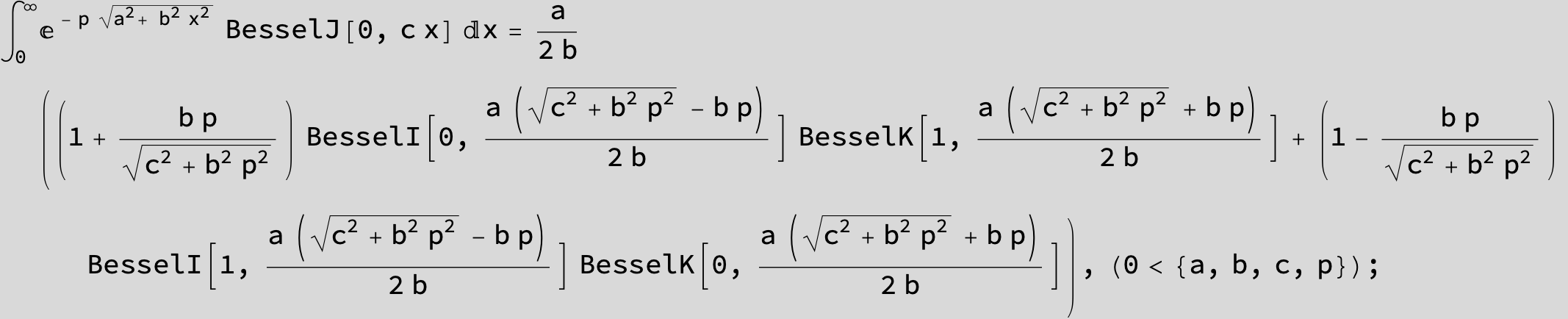
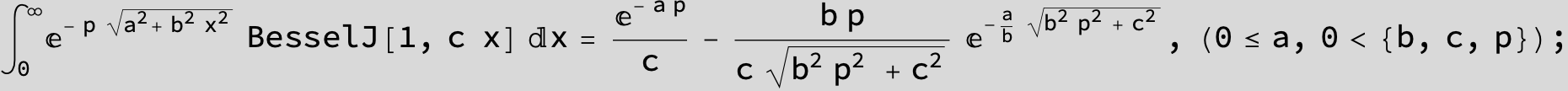
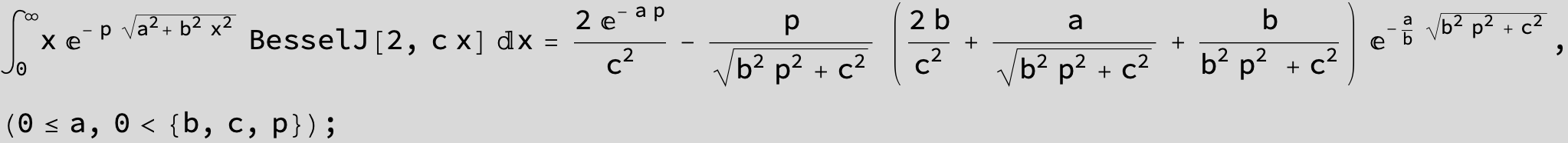
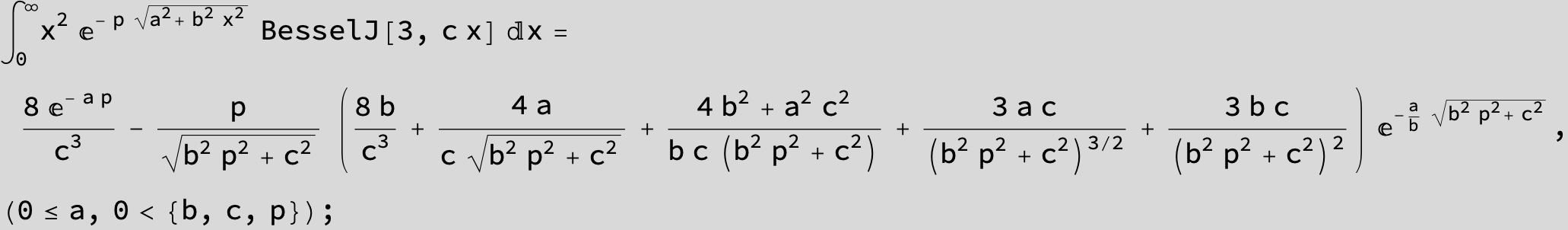
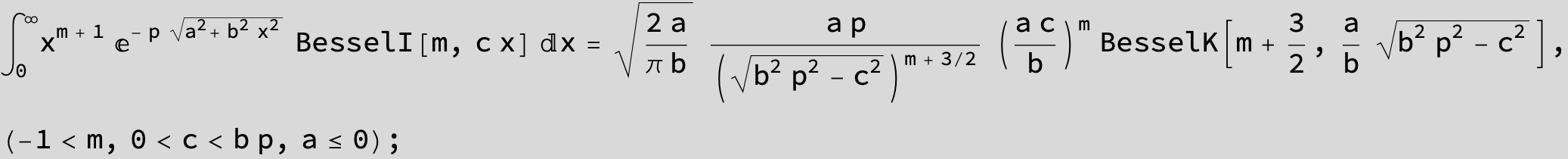
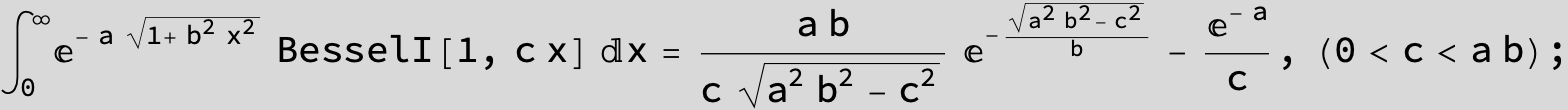
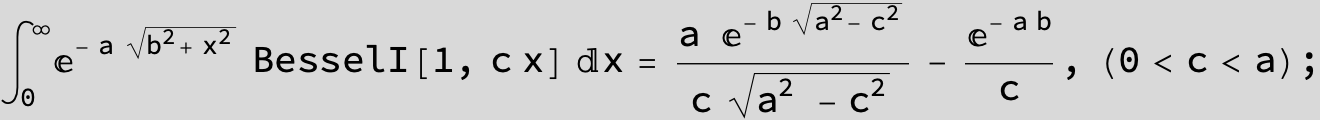
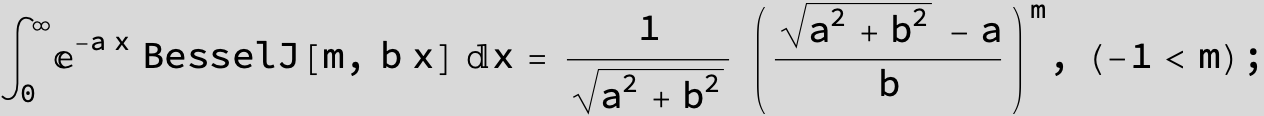
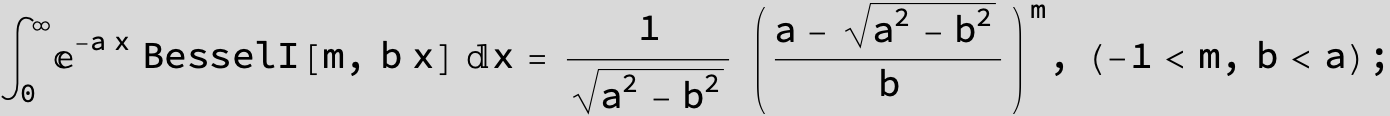
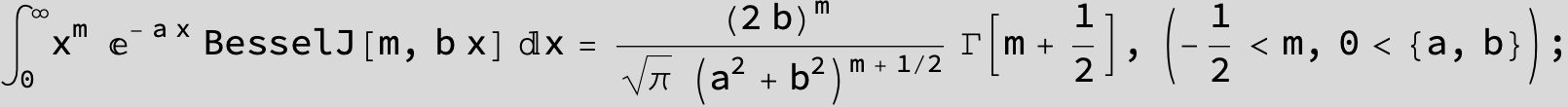
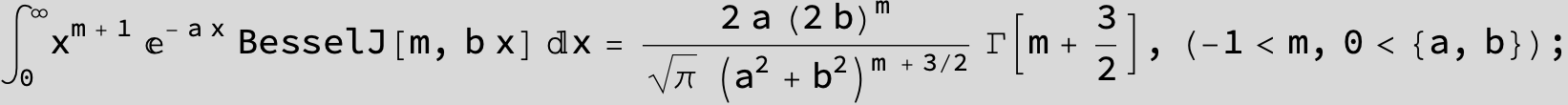
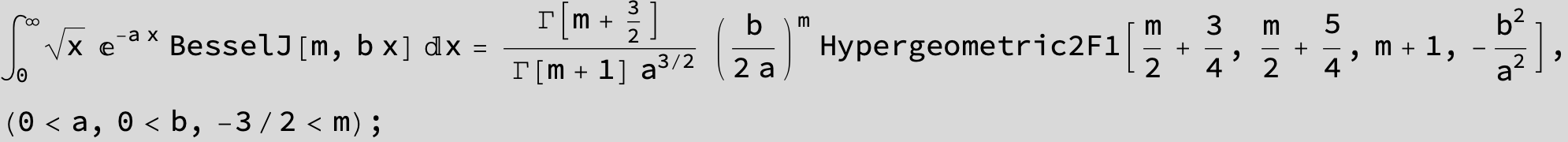
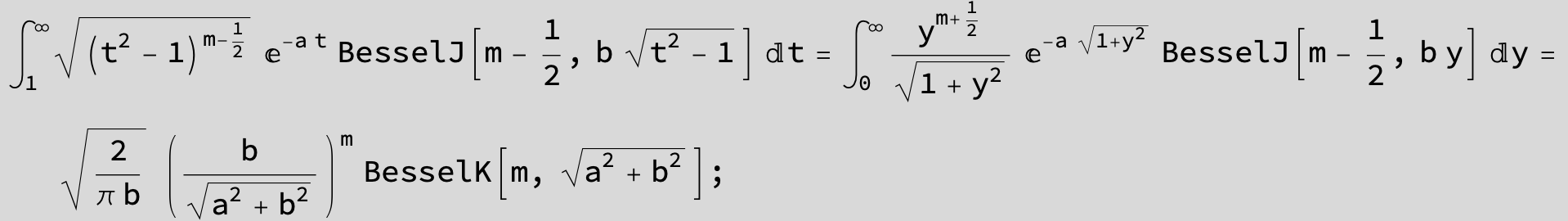
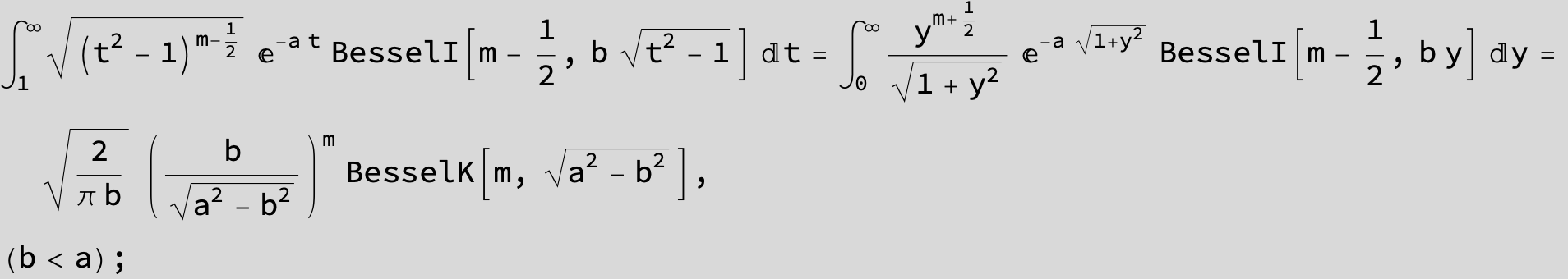
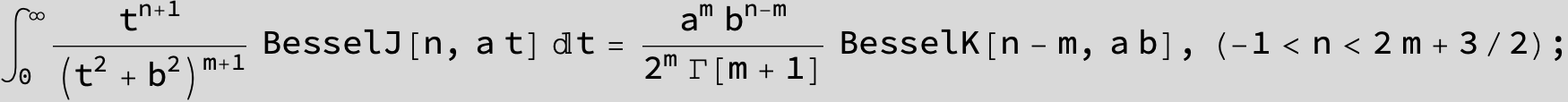
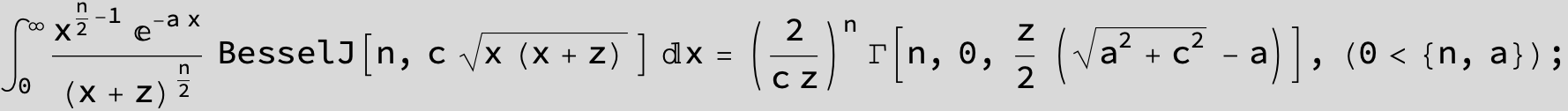
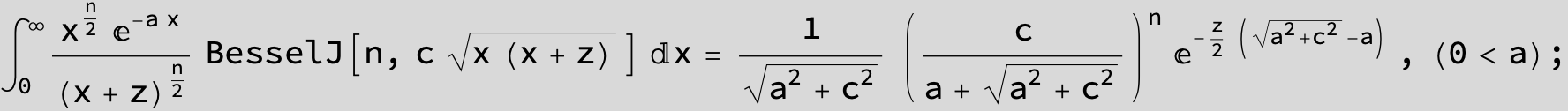
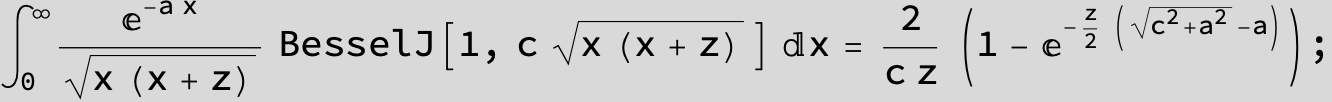
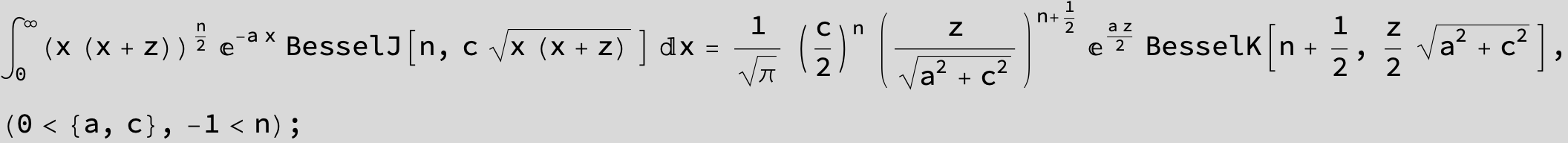
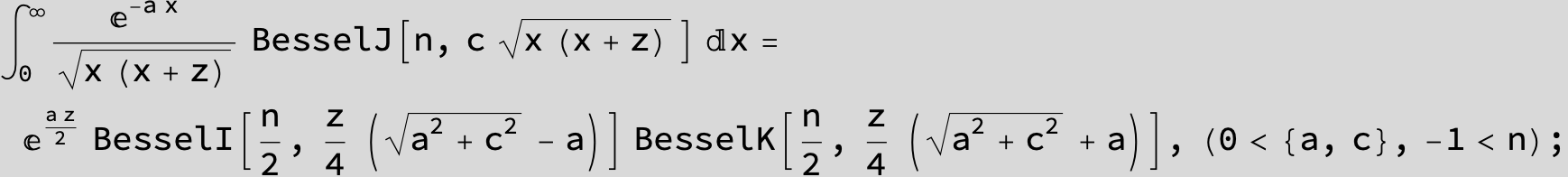
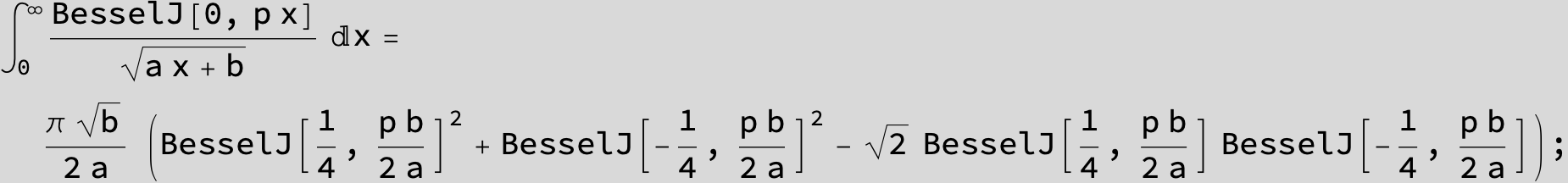
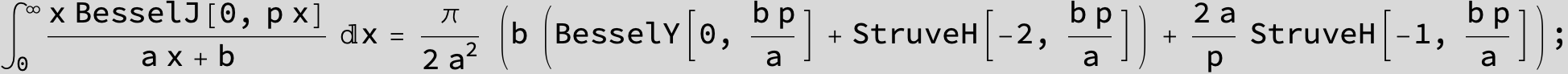
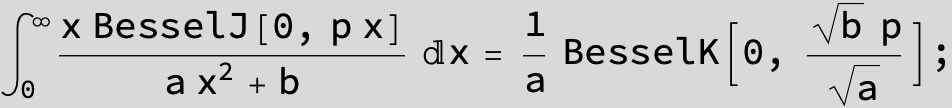
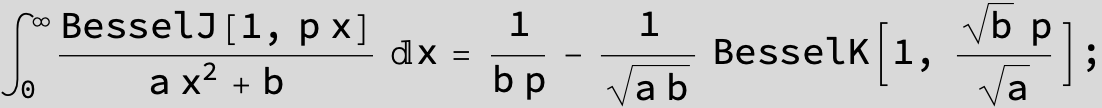
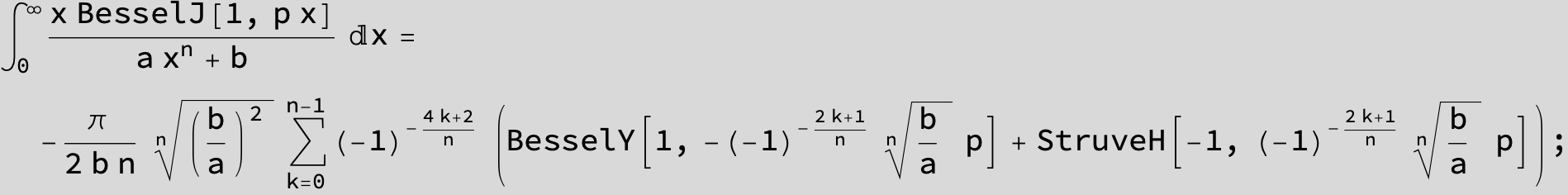
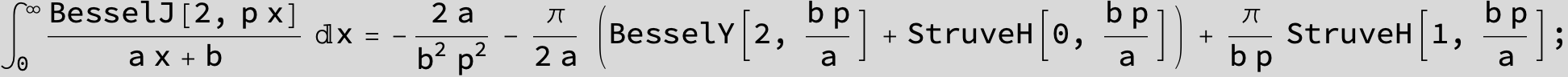
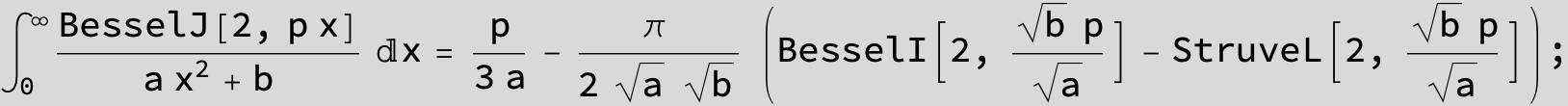
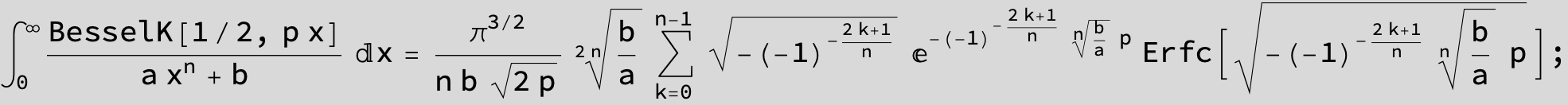
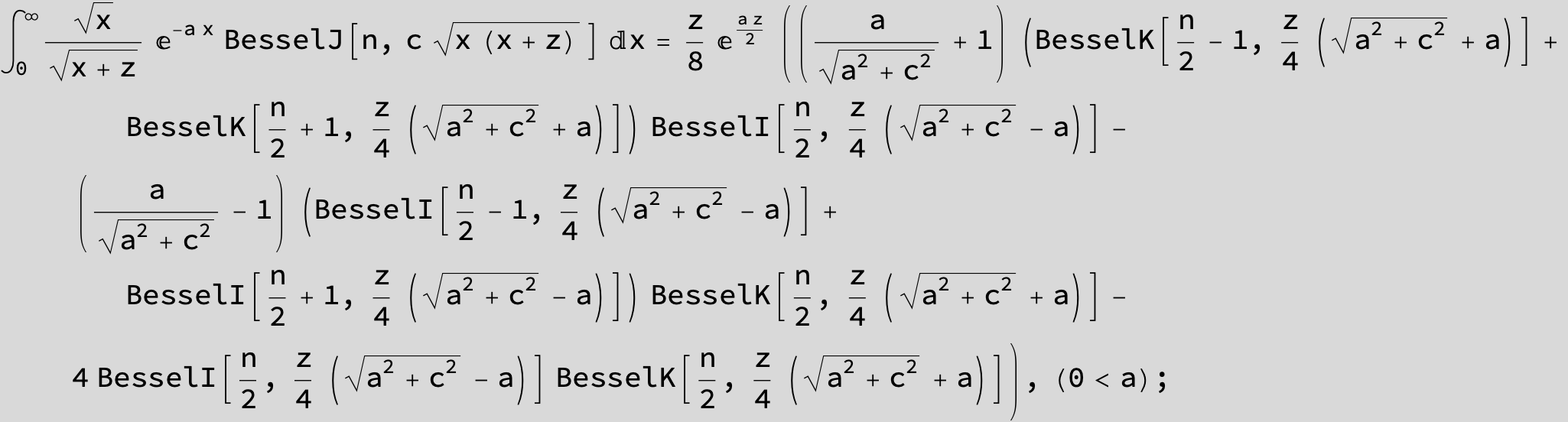
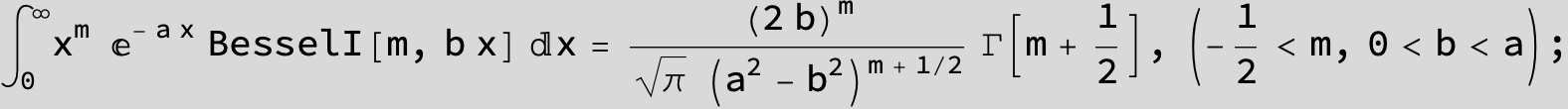
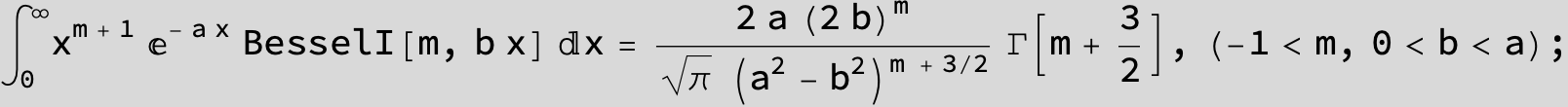
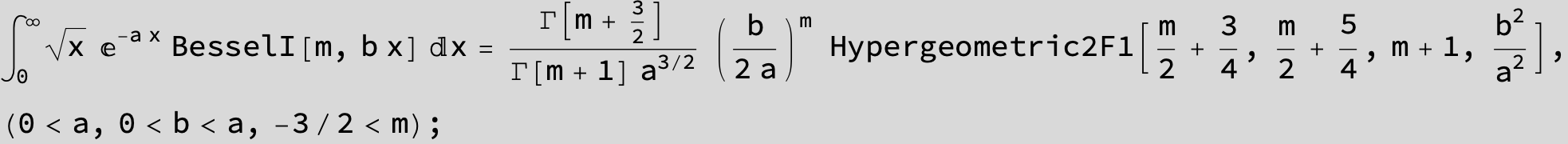
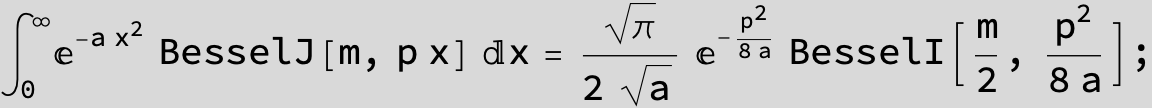
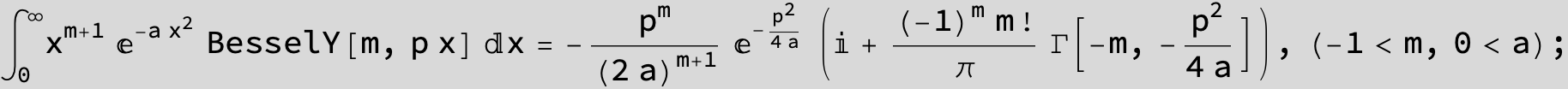
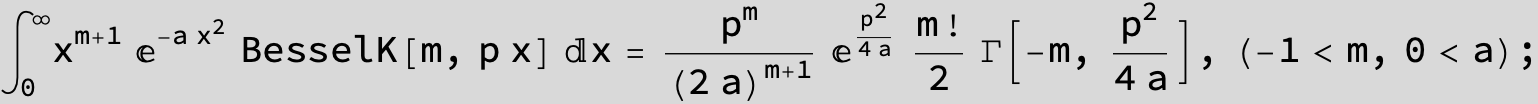
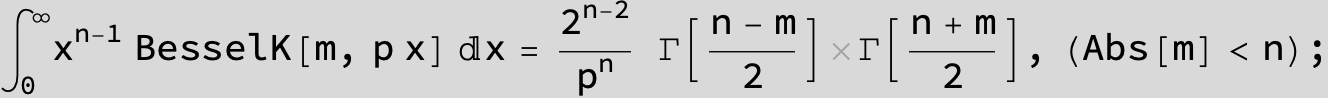
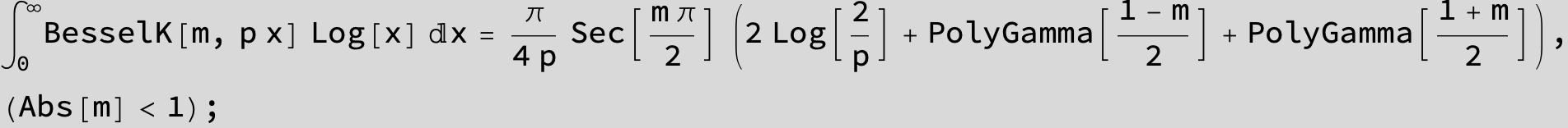
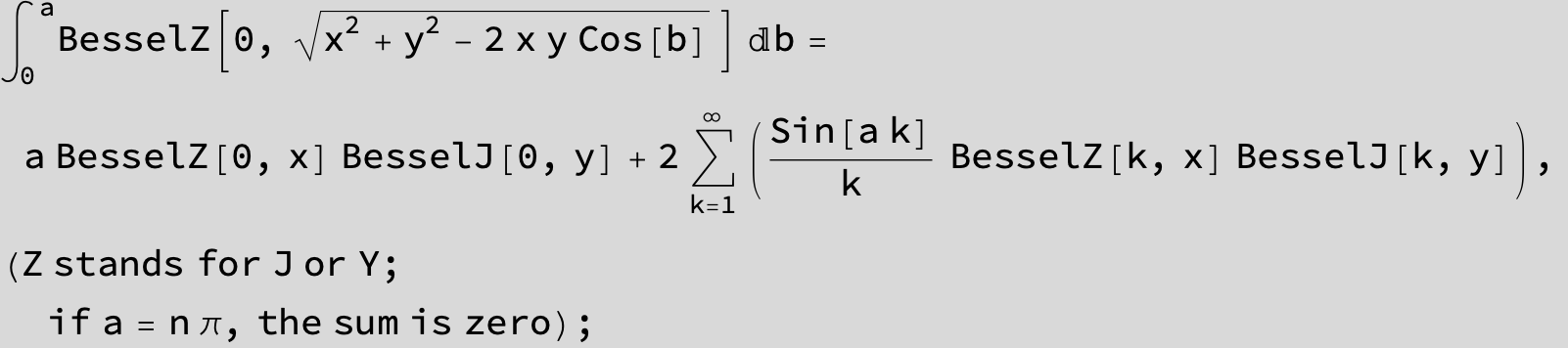
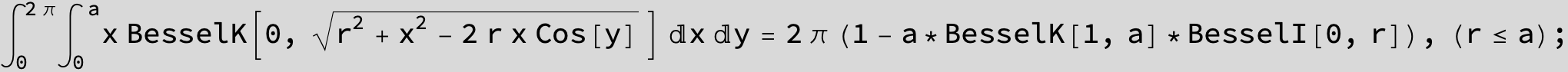
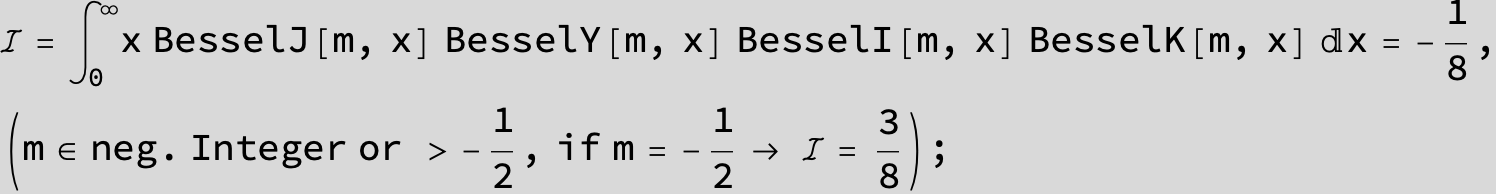
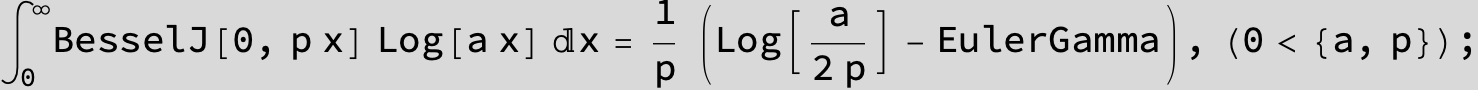
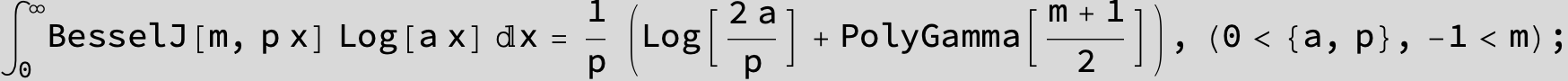
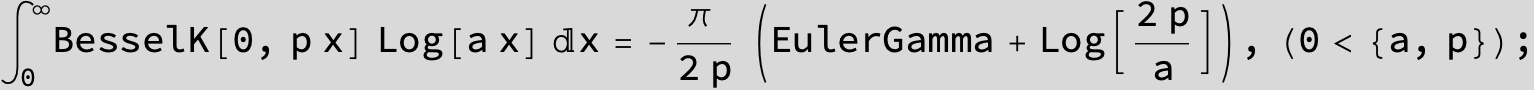
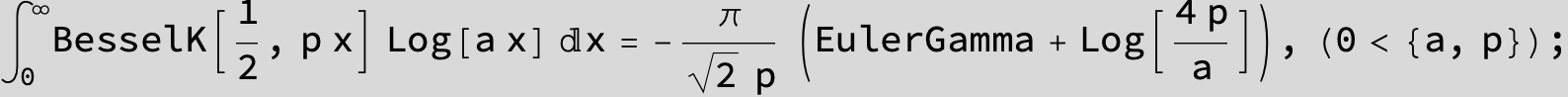
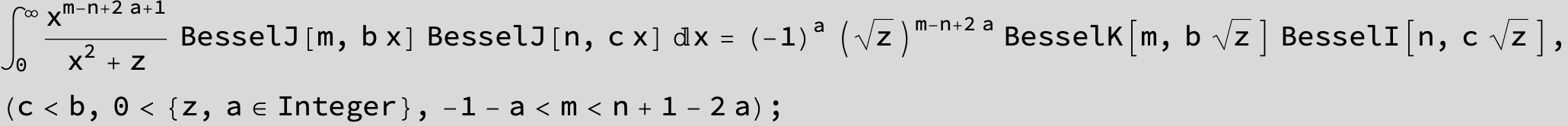
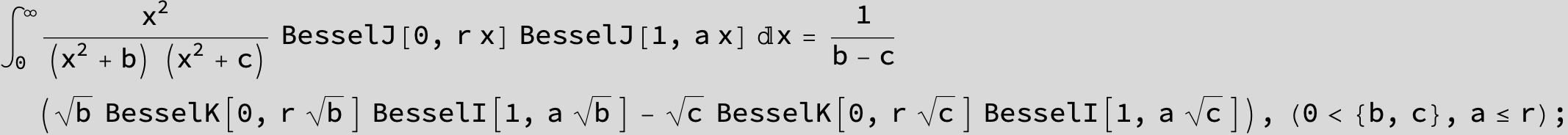
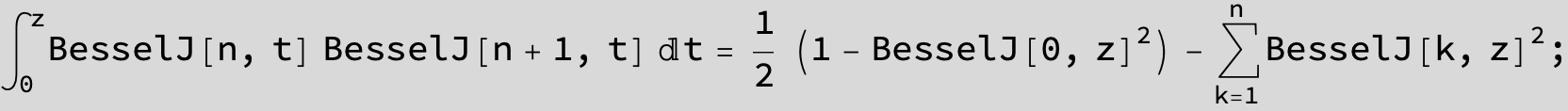
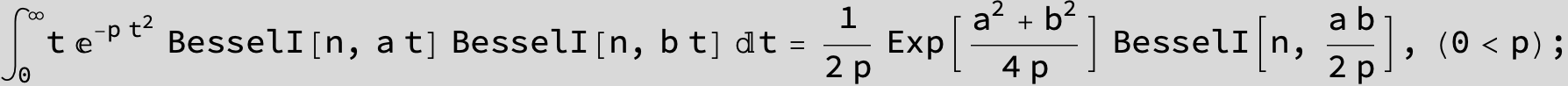
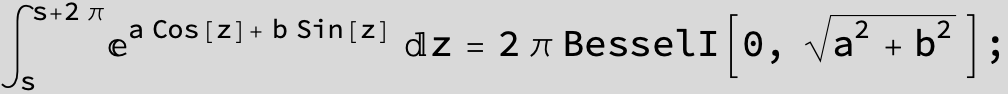
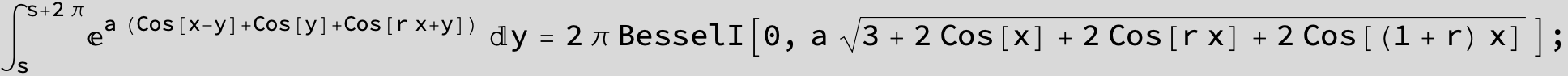
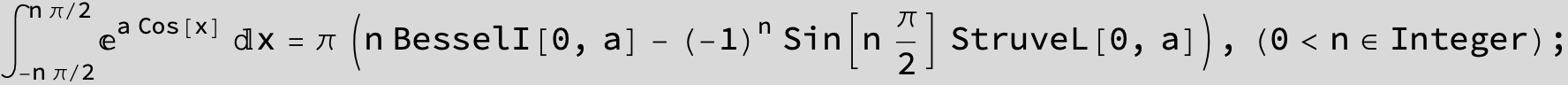
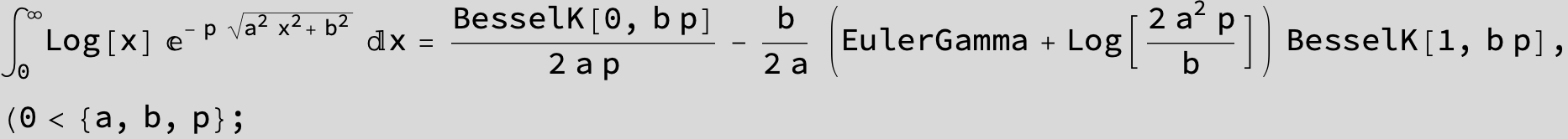
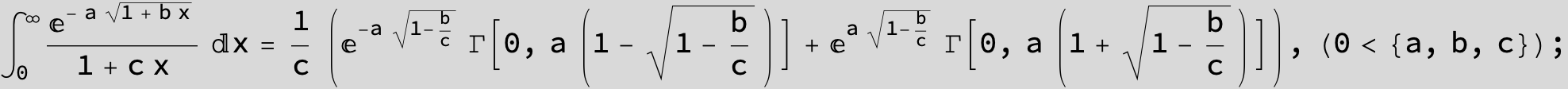
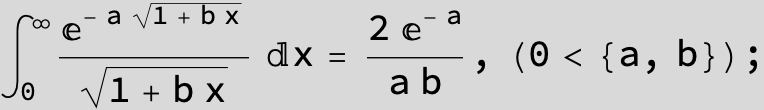
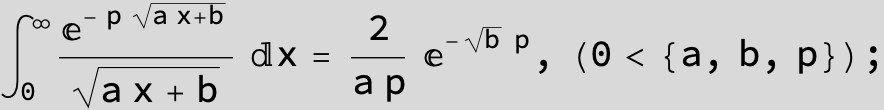
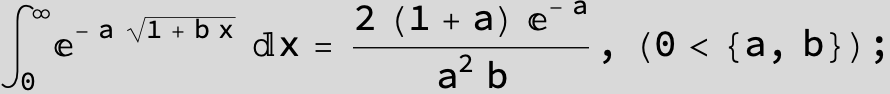
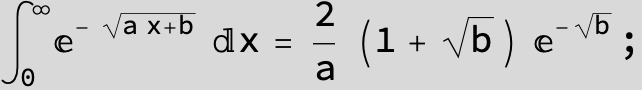
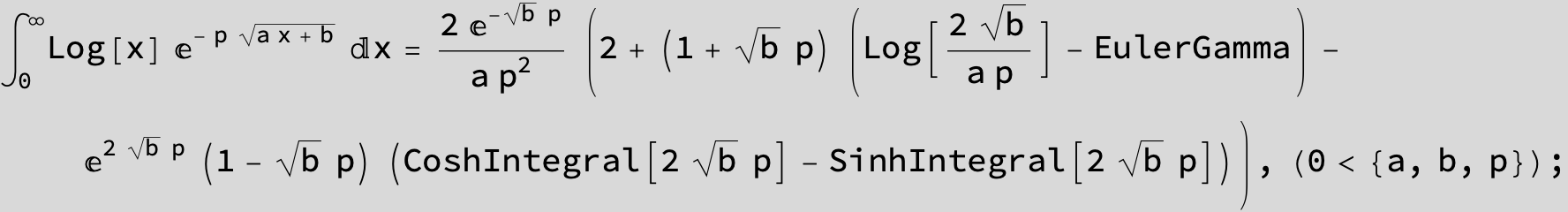
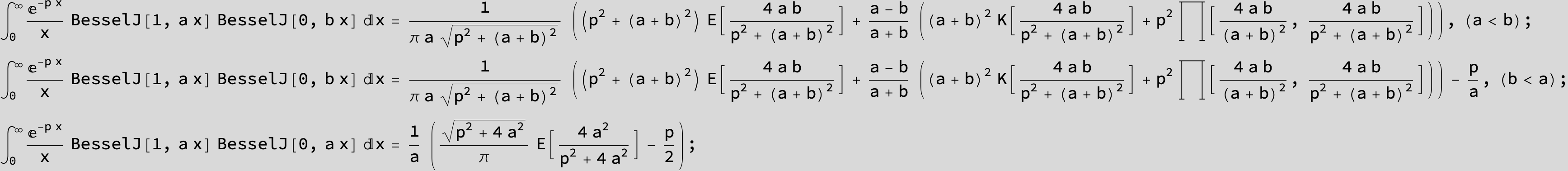
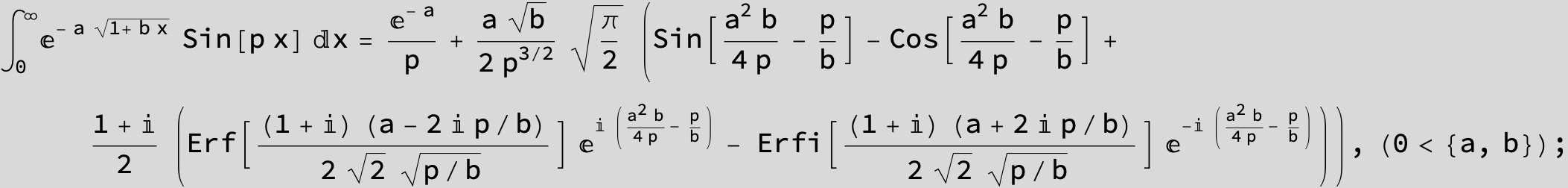
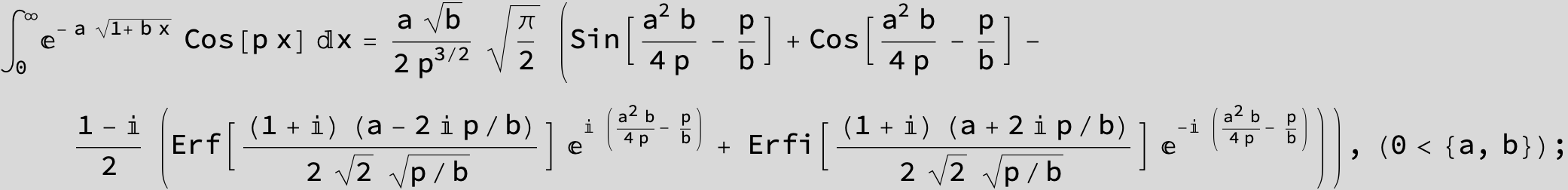
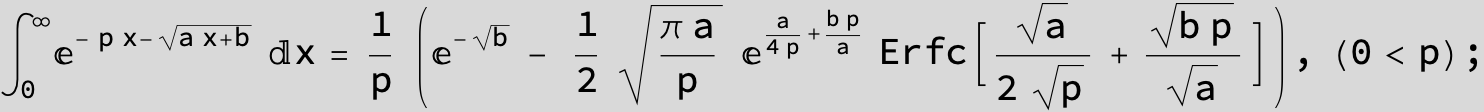
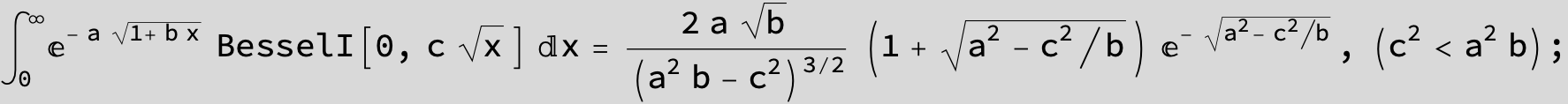
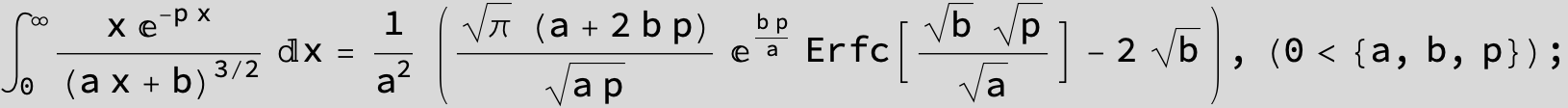
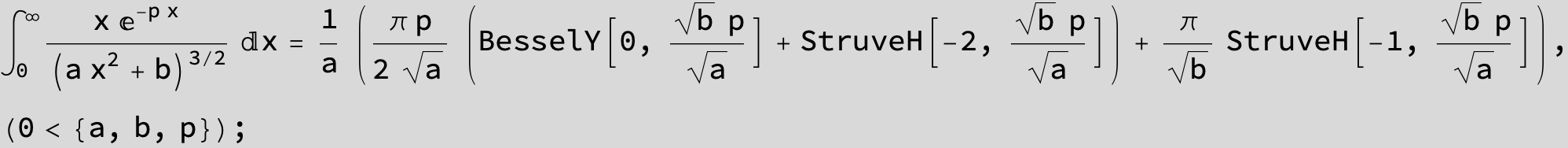
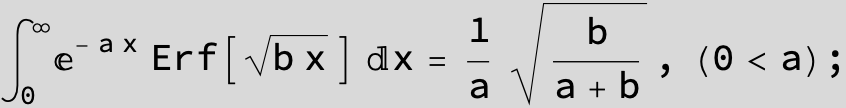
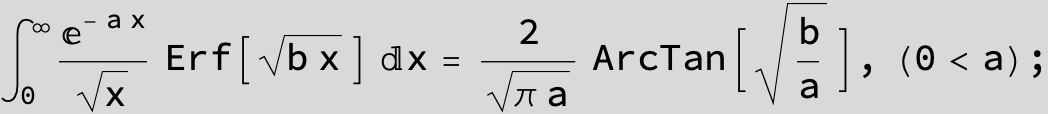
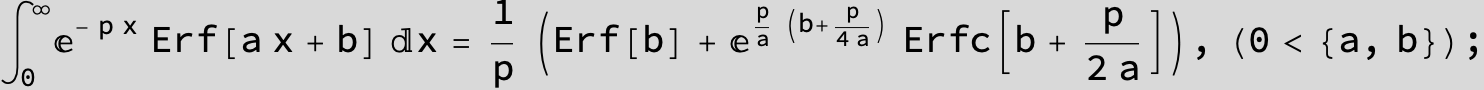
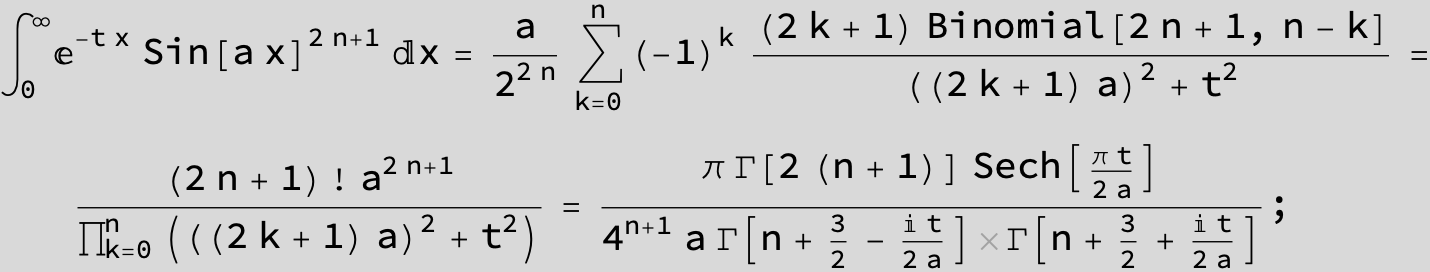
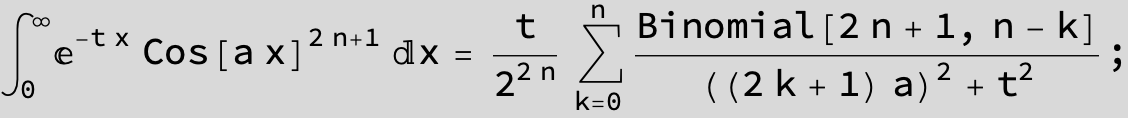
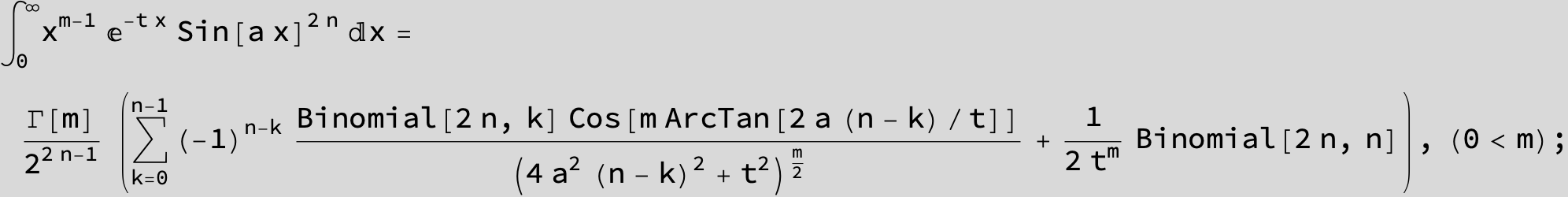
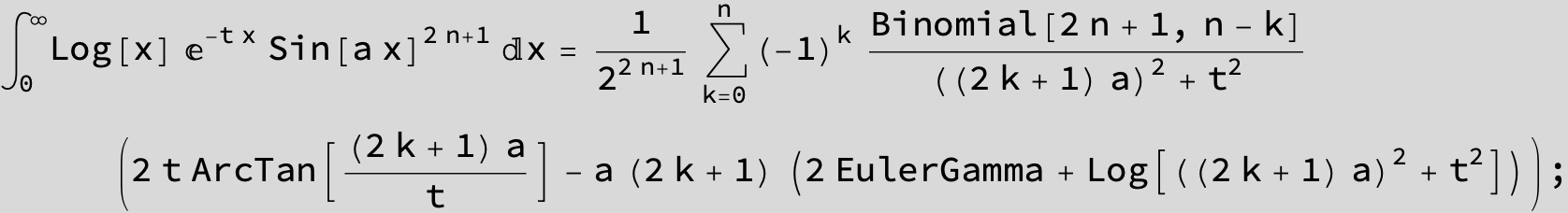
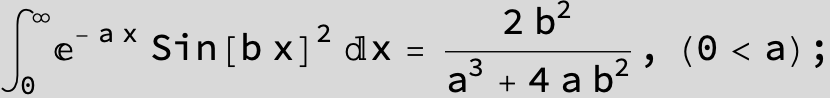
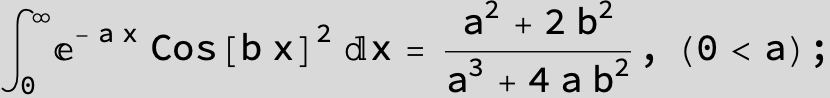
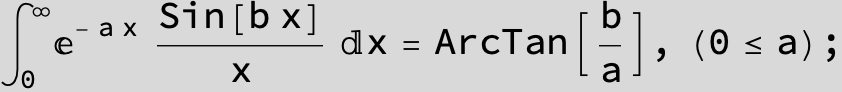
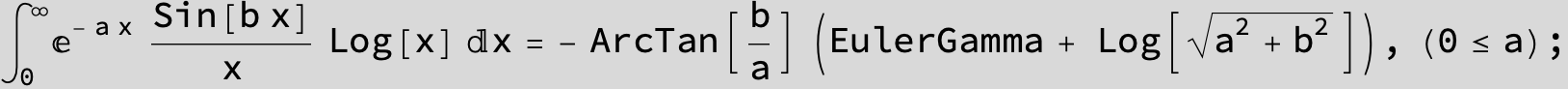
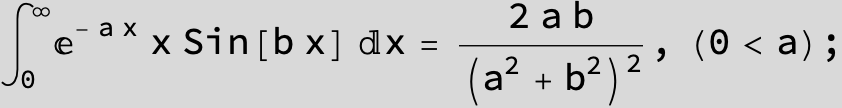
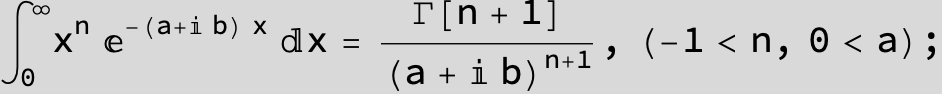
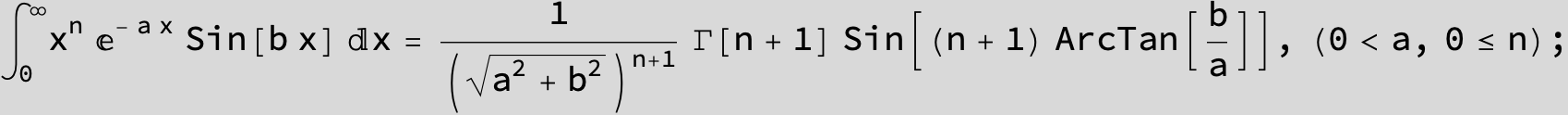
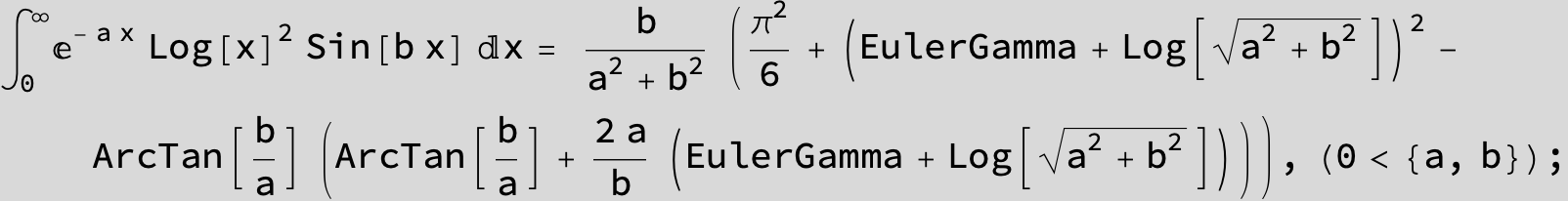
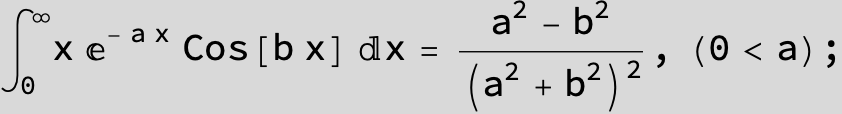
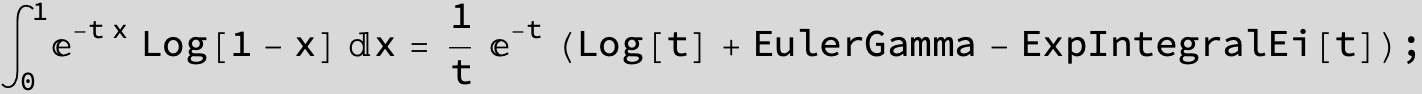
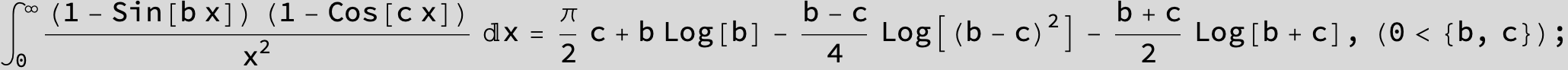
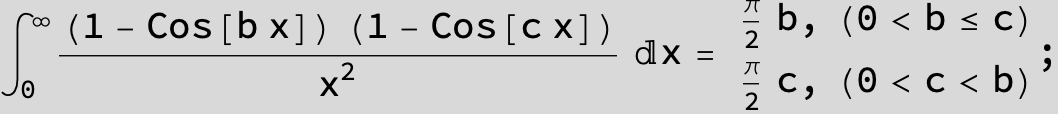
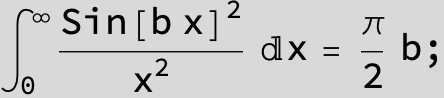
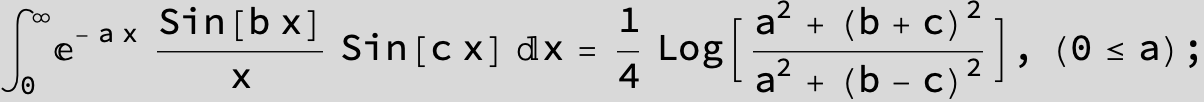
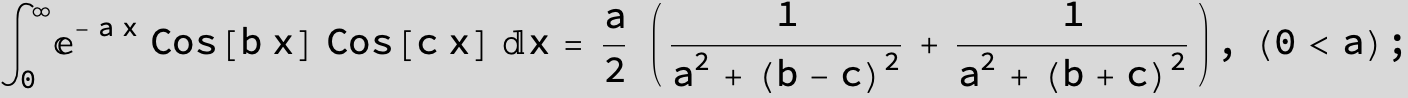
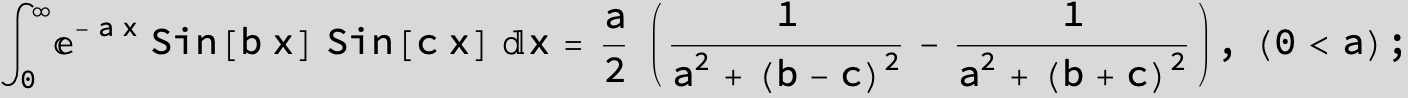
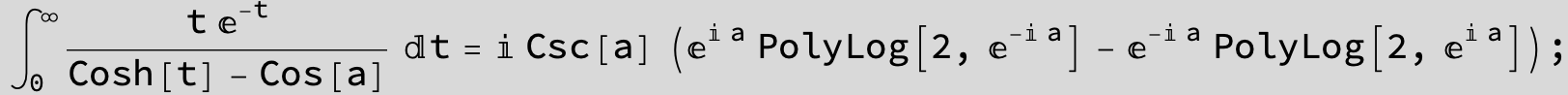
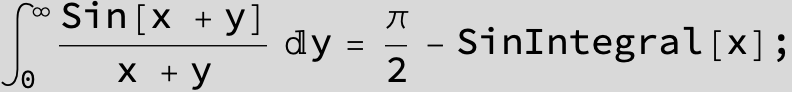
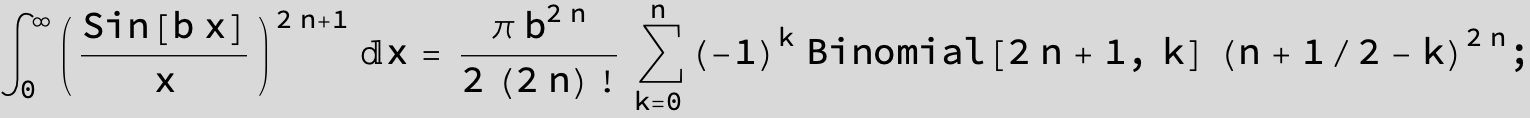
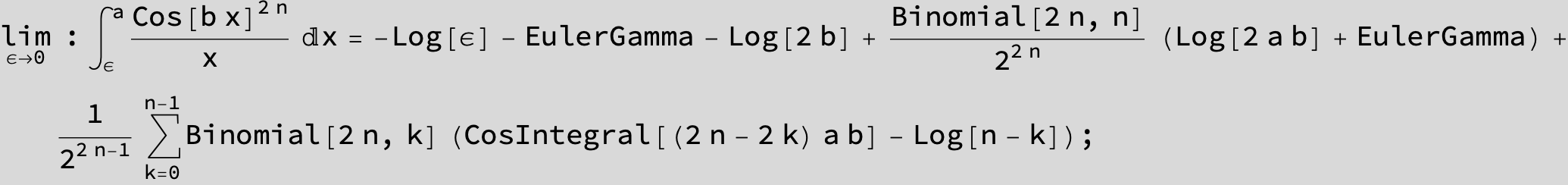
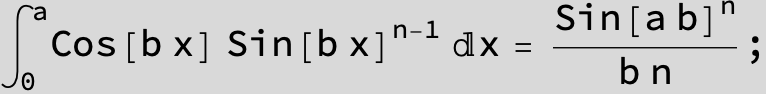
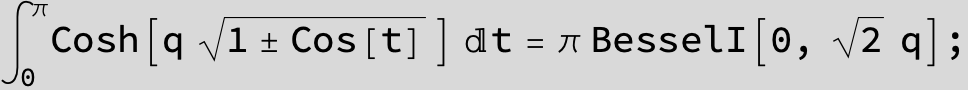
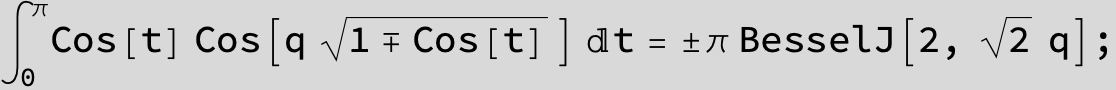
Arclength of of a helix around a torus with major radius R, minor radius r and number of windings n :

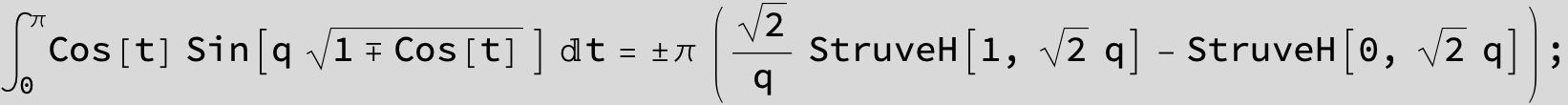
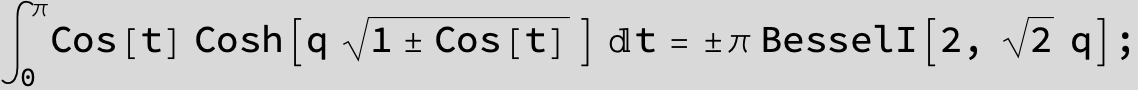
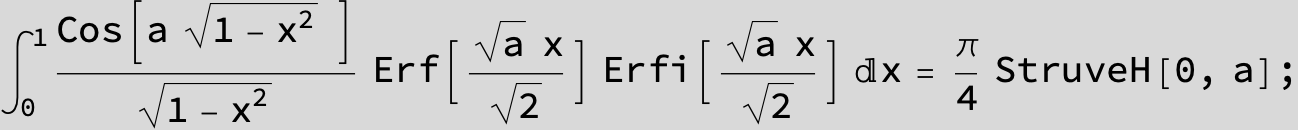
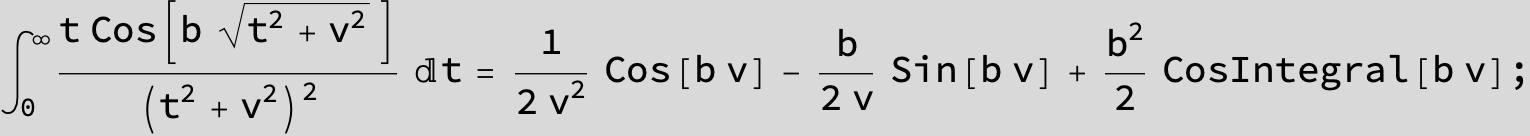
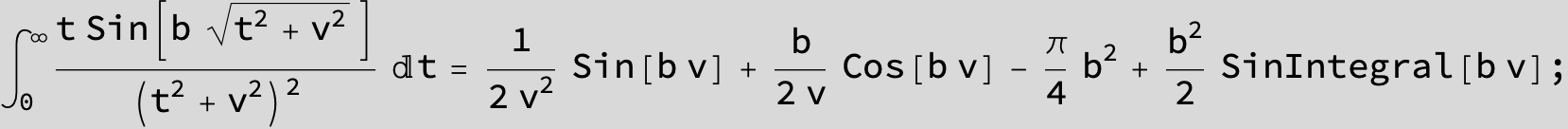
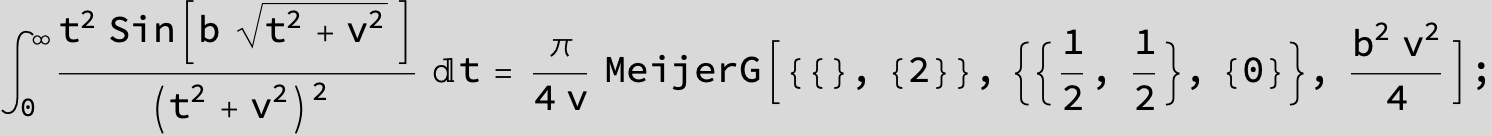
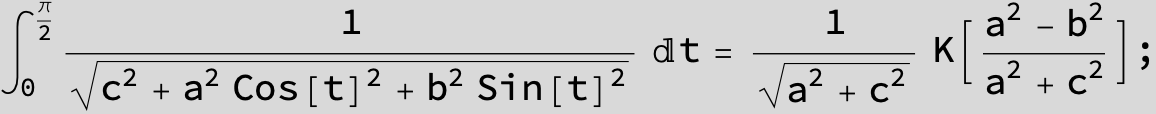
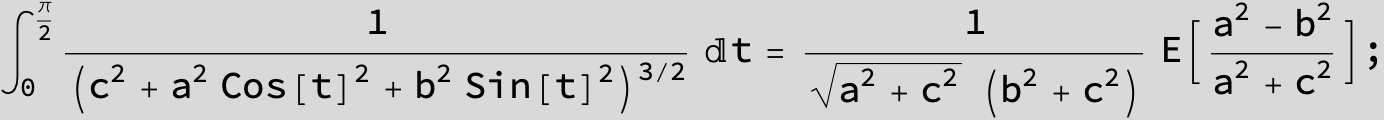
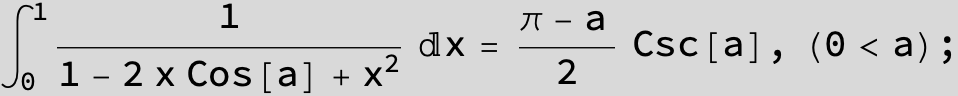
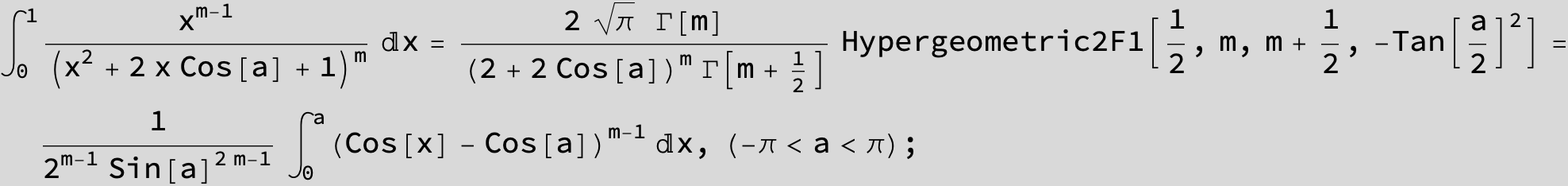
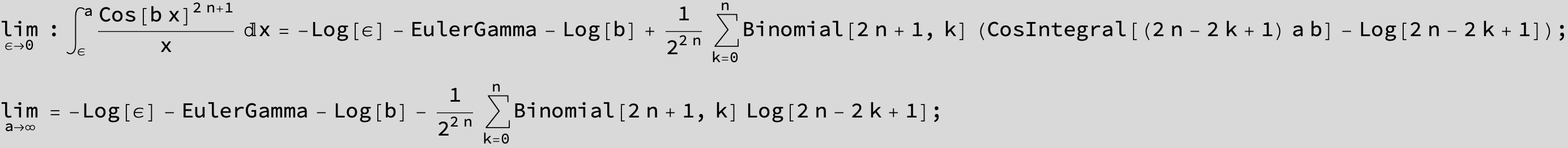
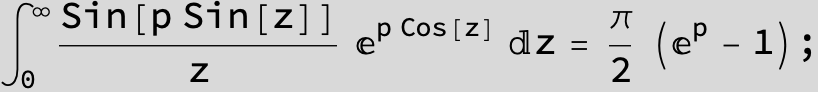
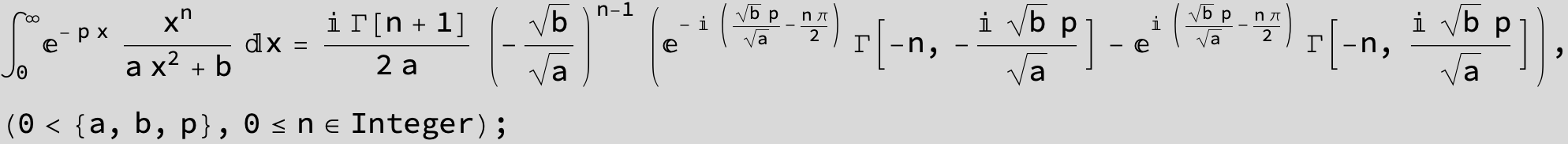
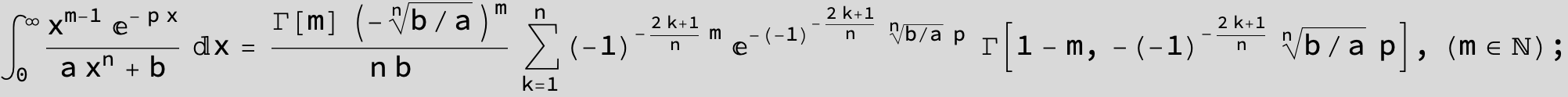
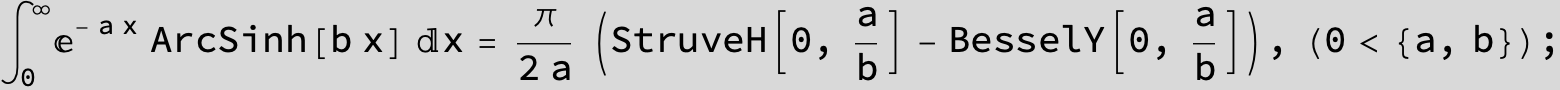
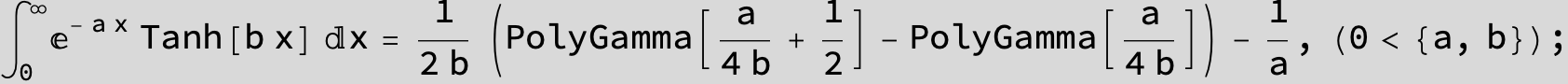
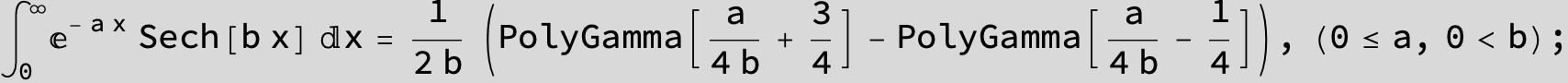
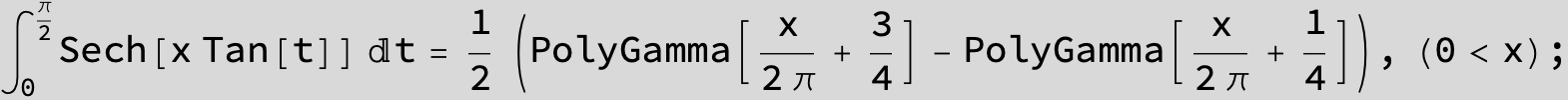
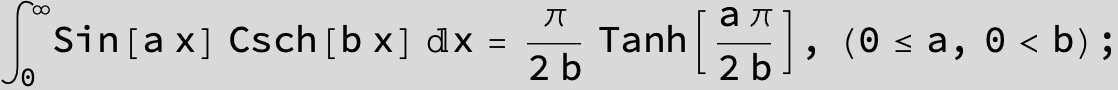
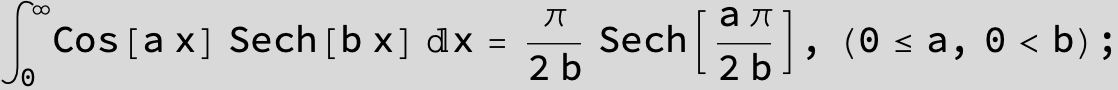
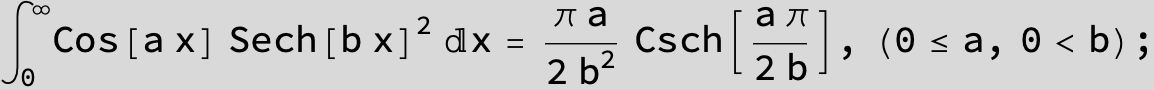
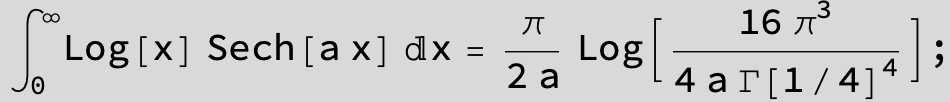
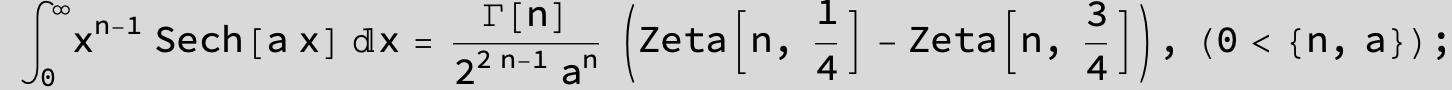
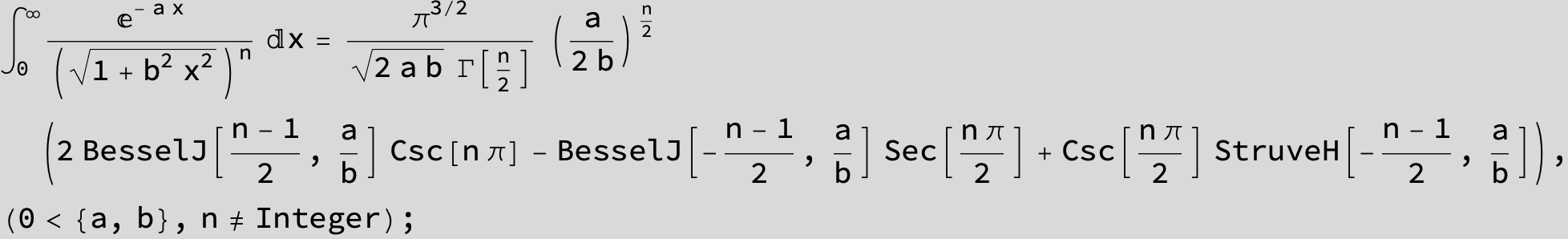
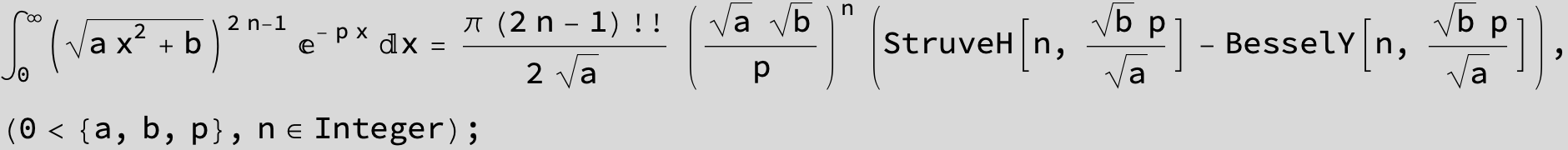
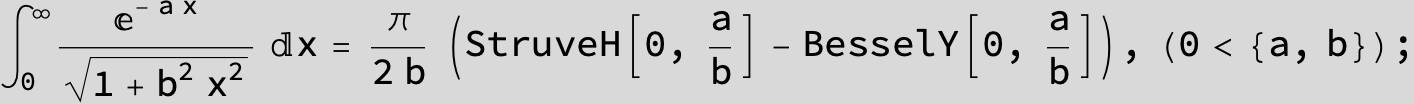
--  4 times the above integral gives the circumference of Cassini' s curve  --

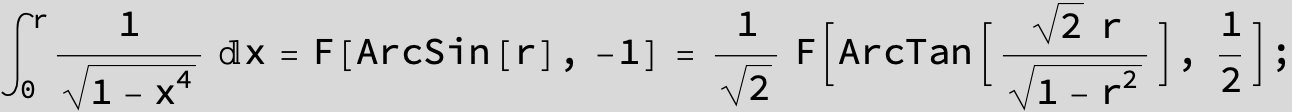
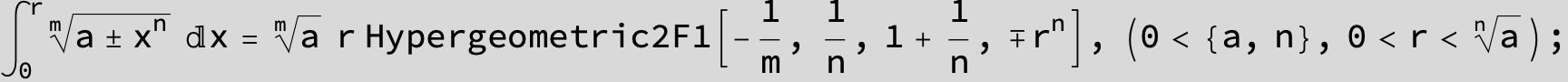
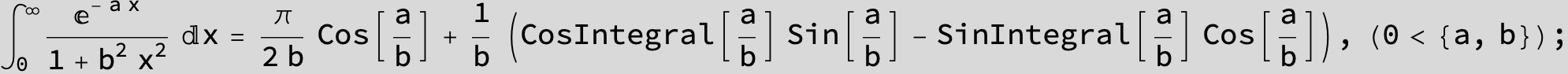
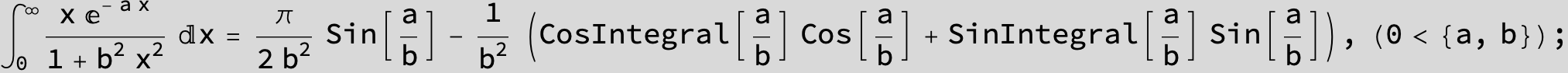
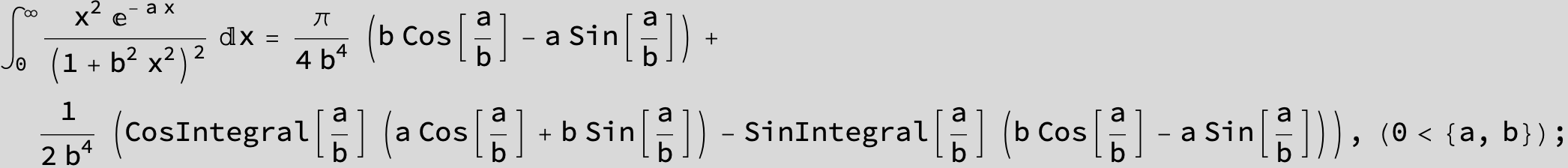
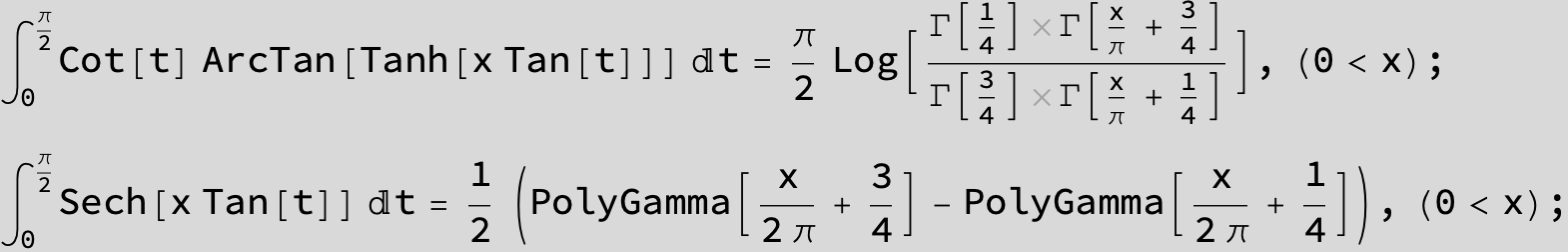
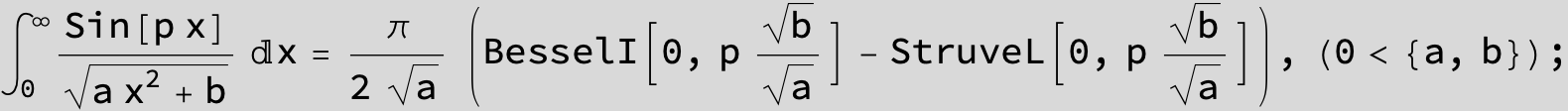
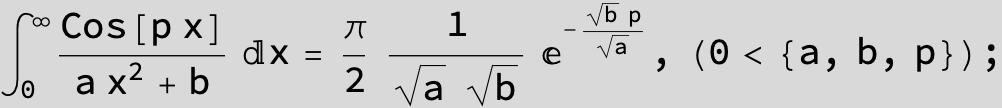
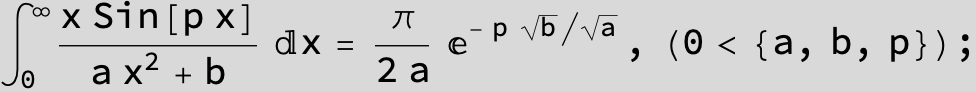
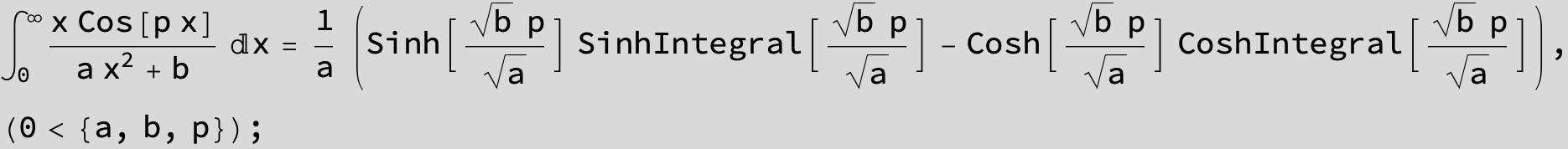
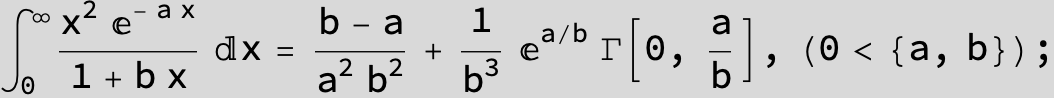
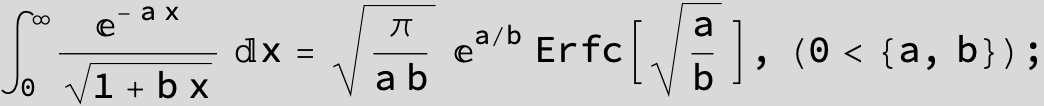
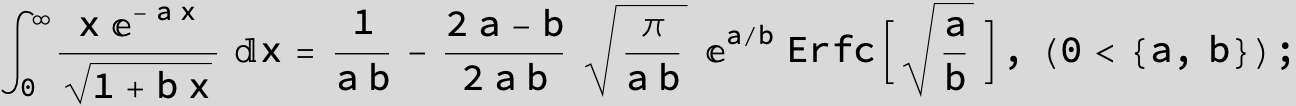
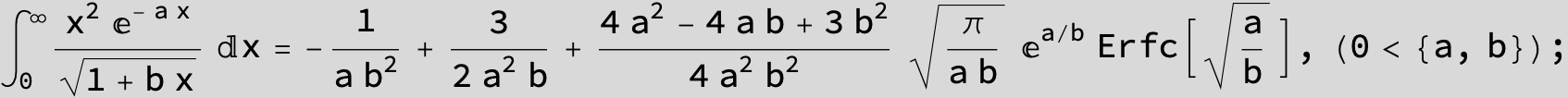
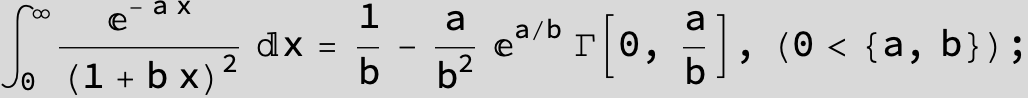
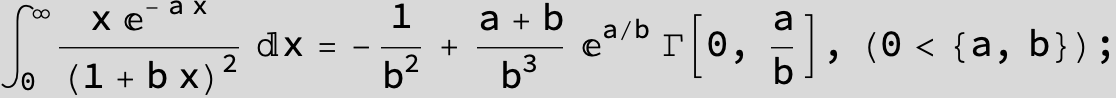
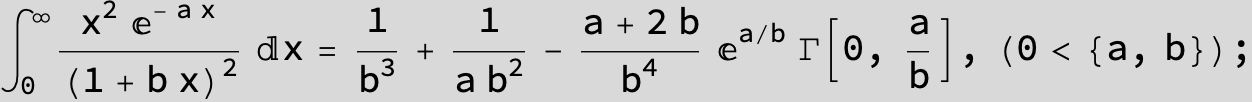
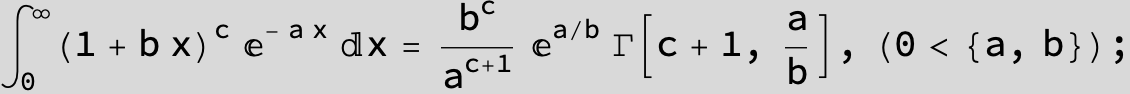
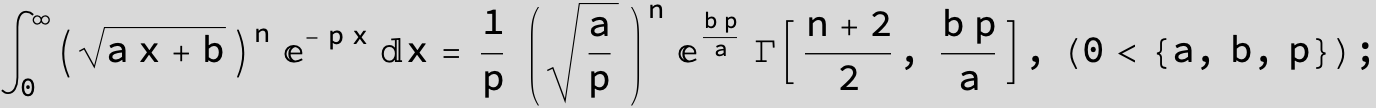
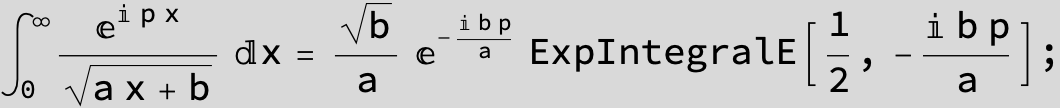
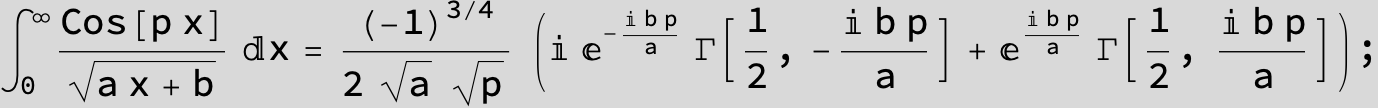
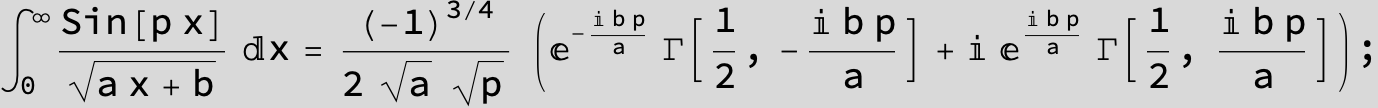
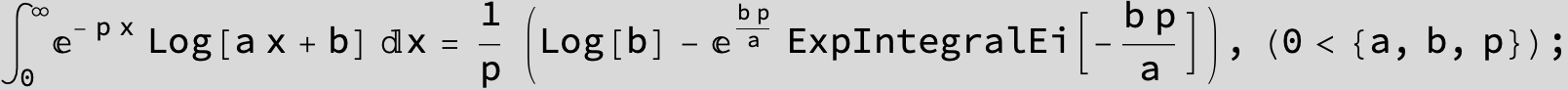
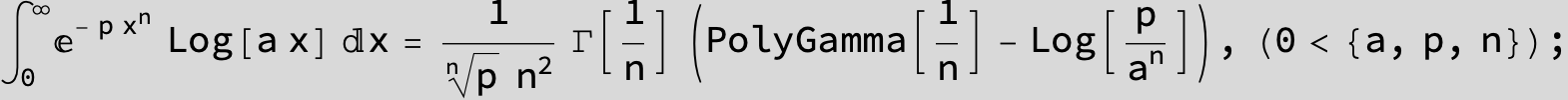
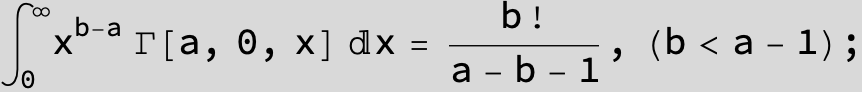
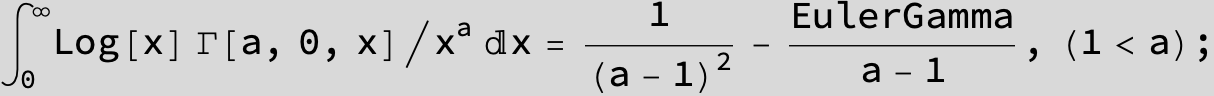
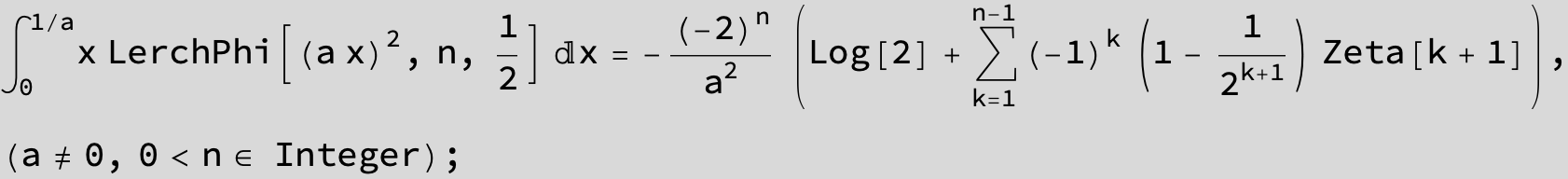
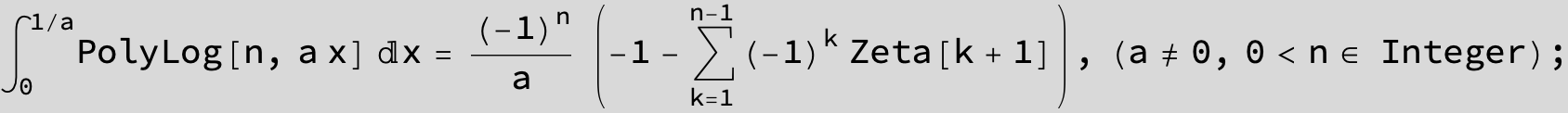
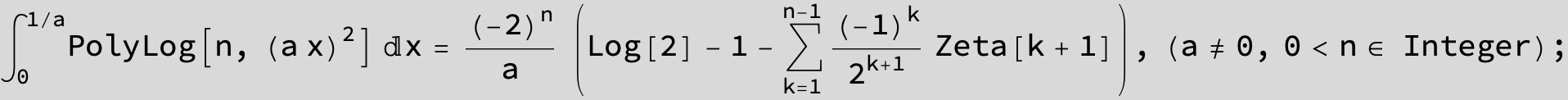
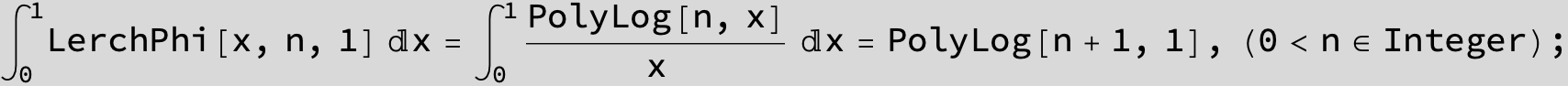
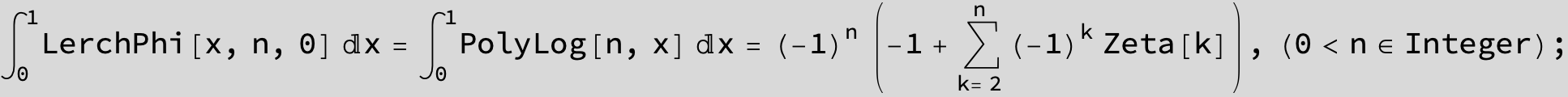
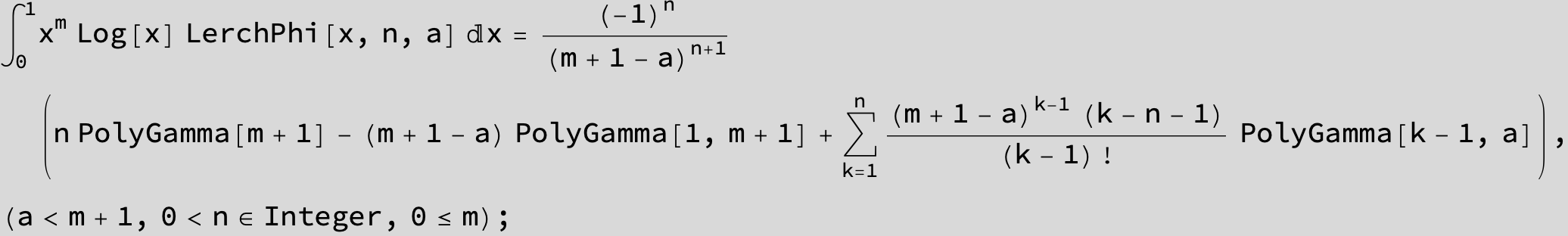
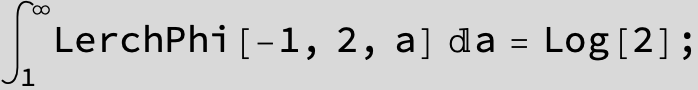
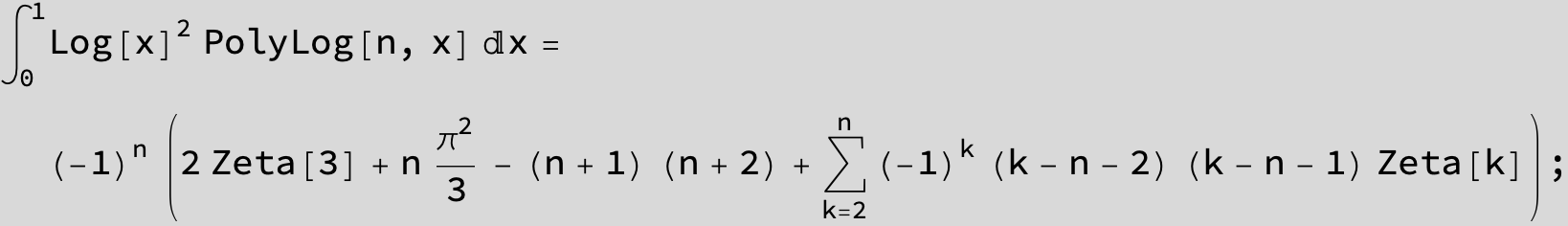
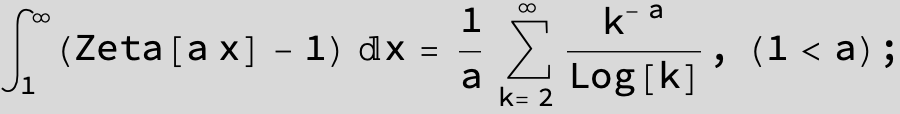
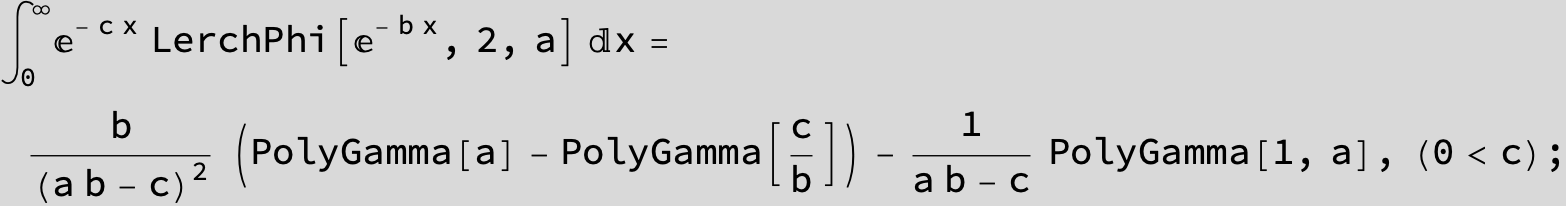
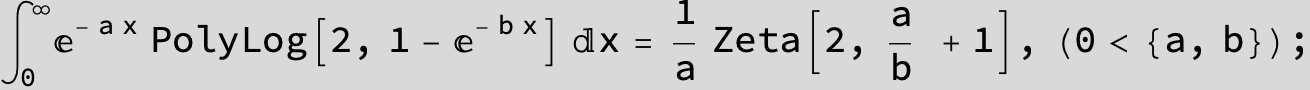
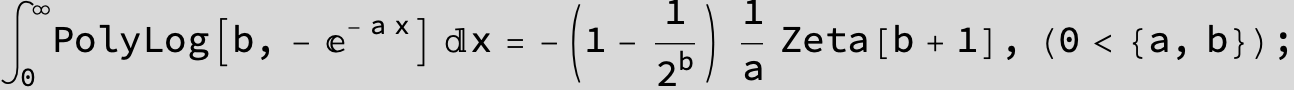
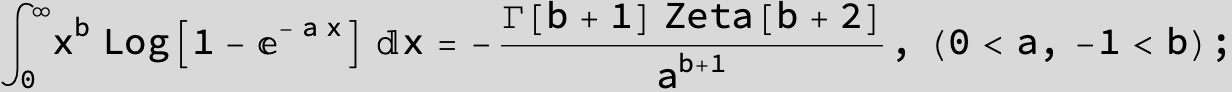
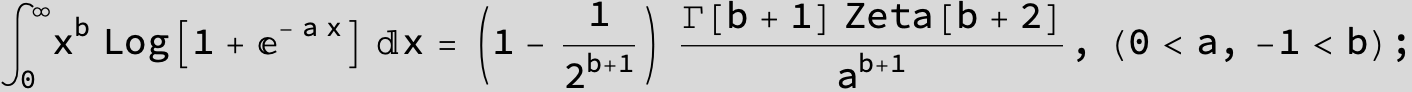
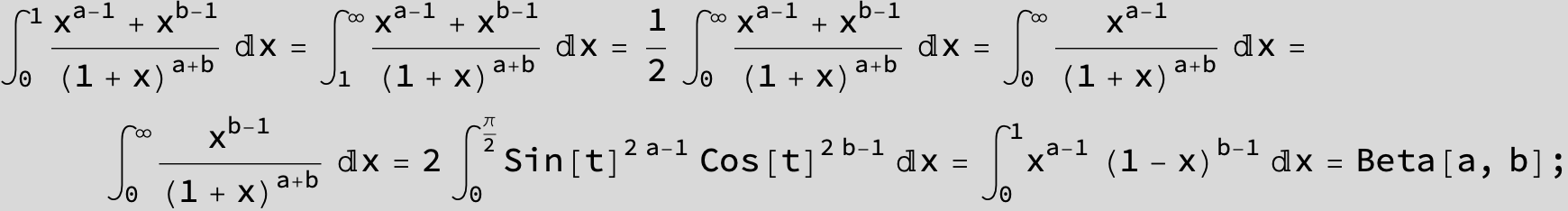
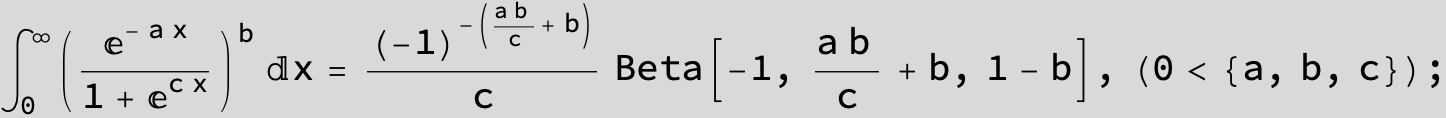
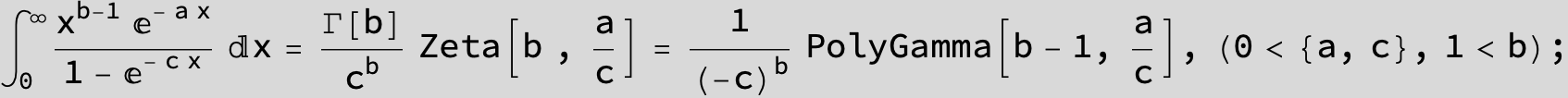
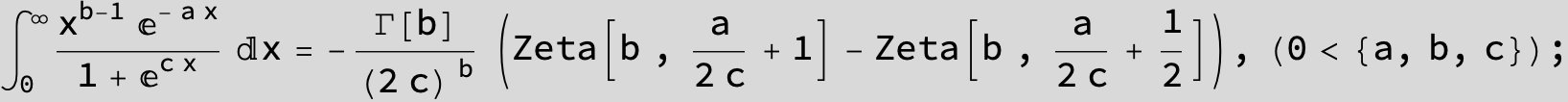
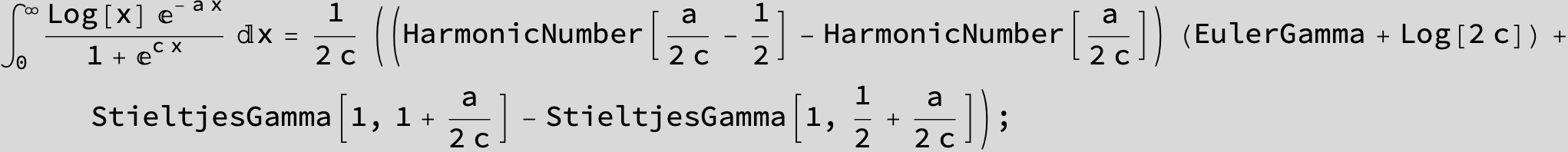
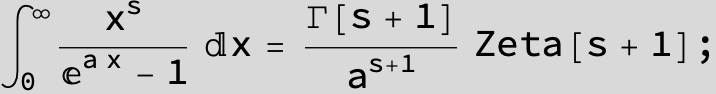
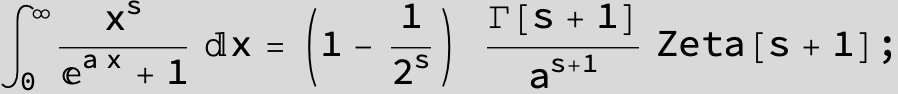
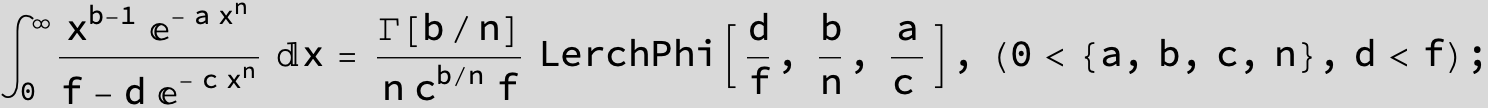
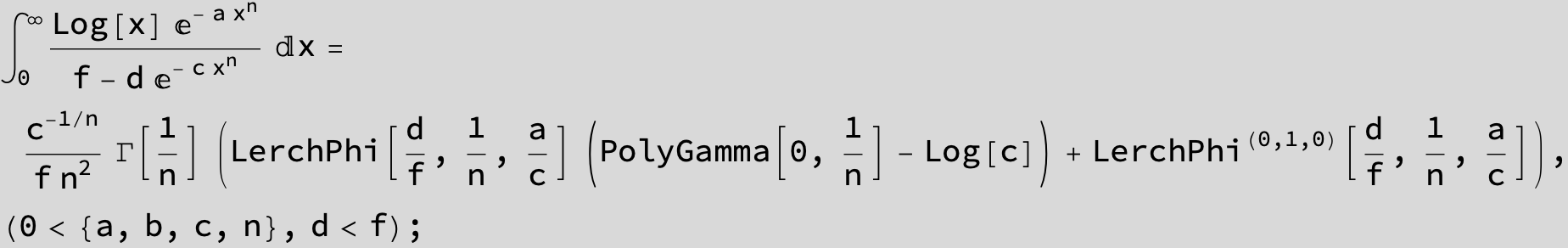
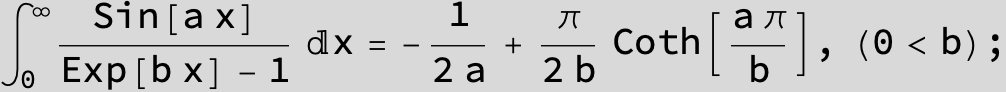
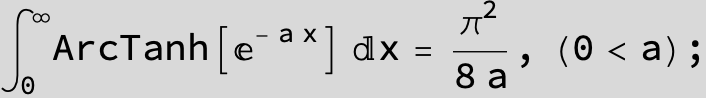
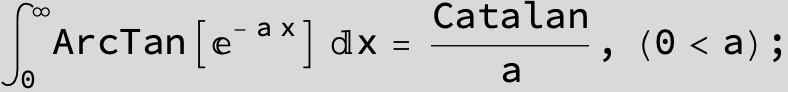
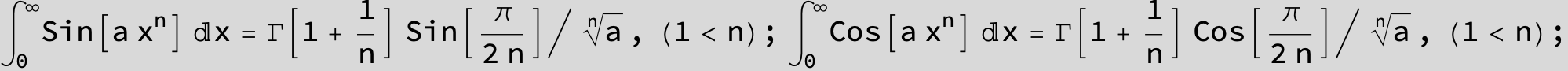
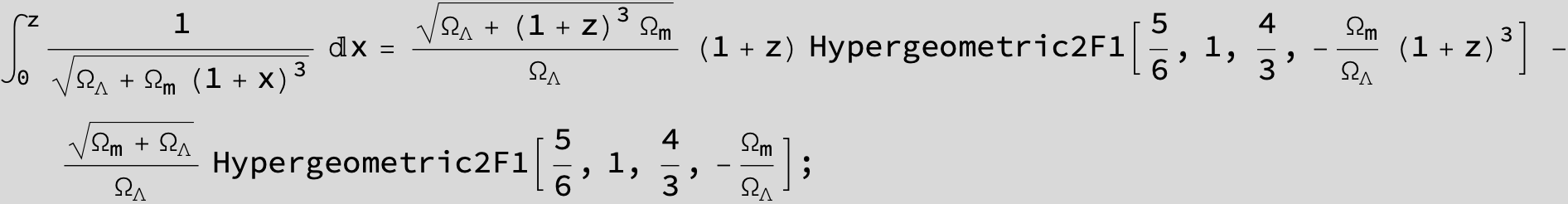
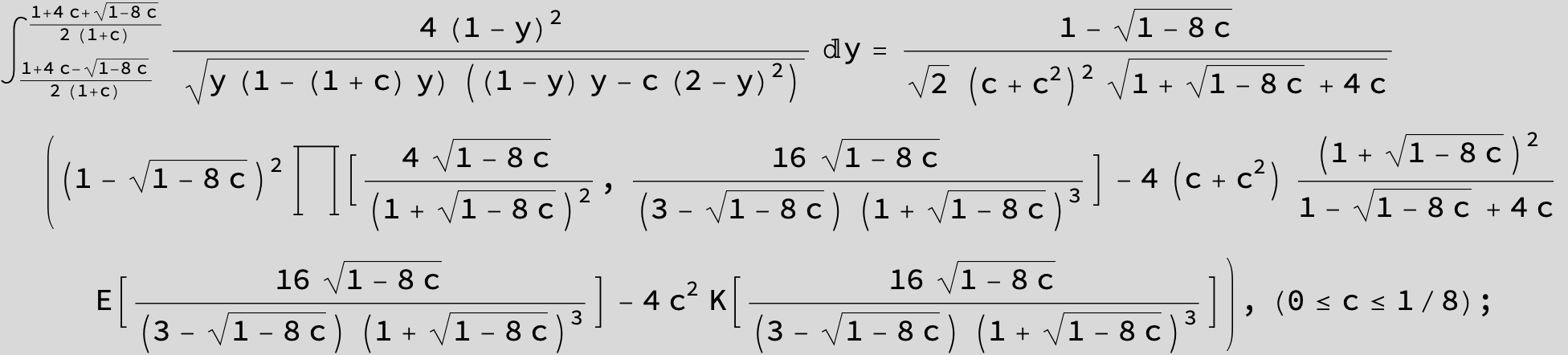
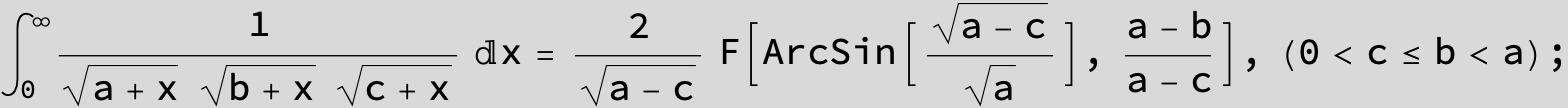
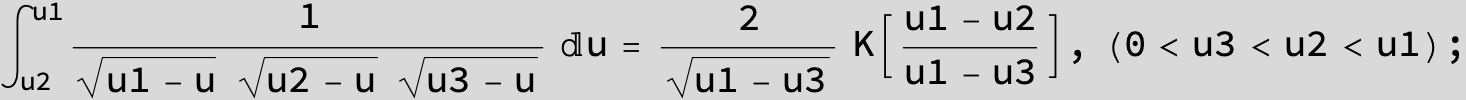
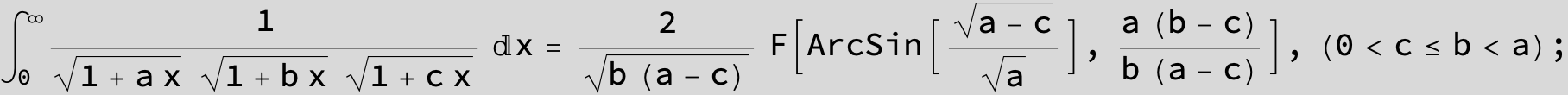
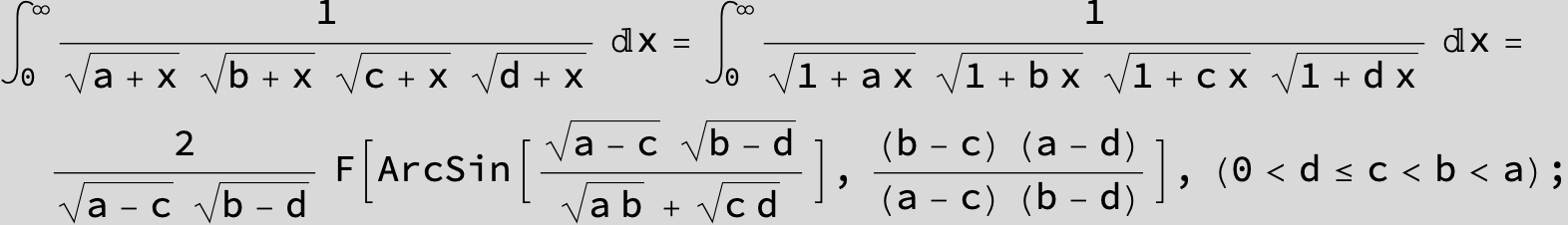
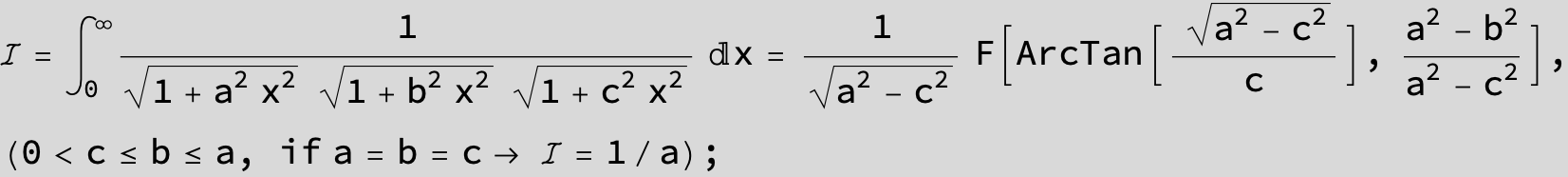
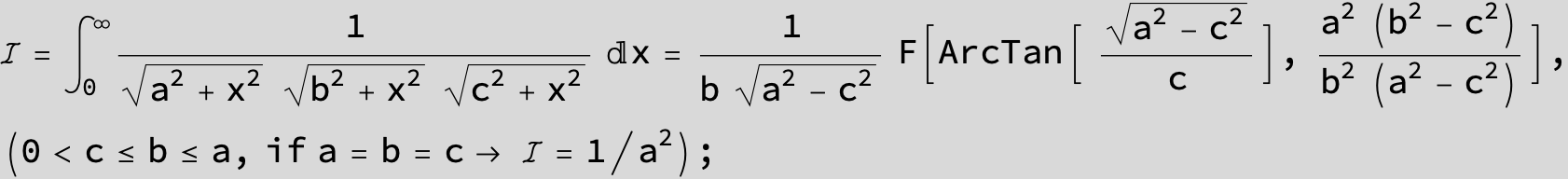
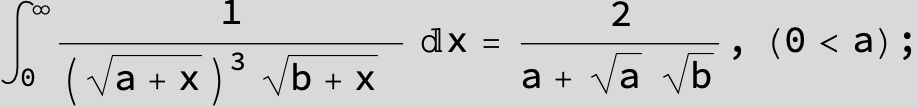
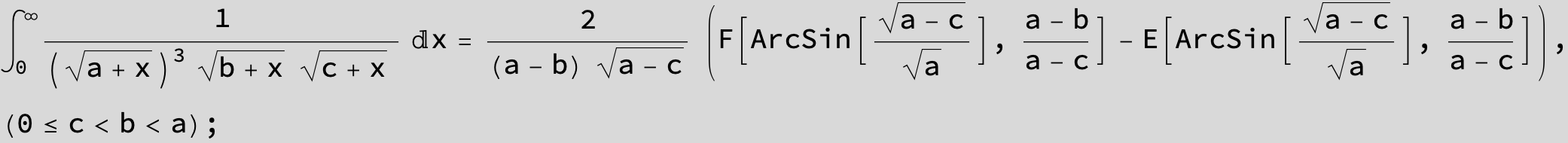
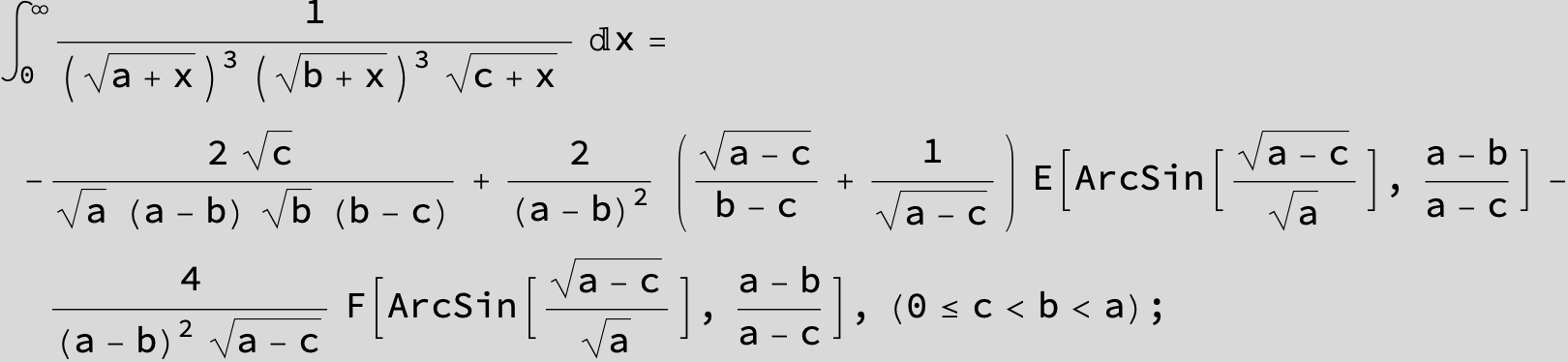
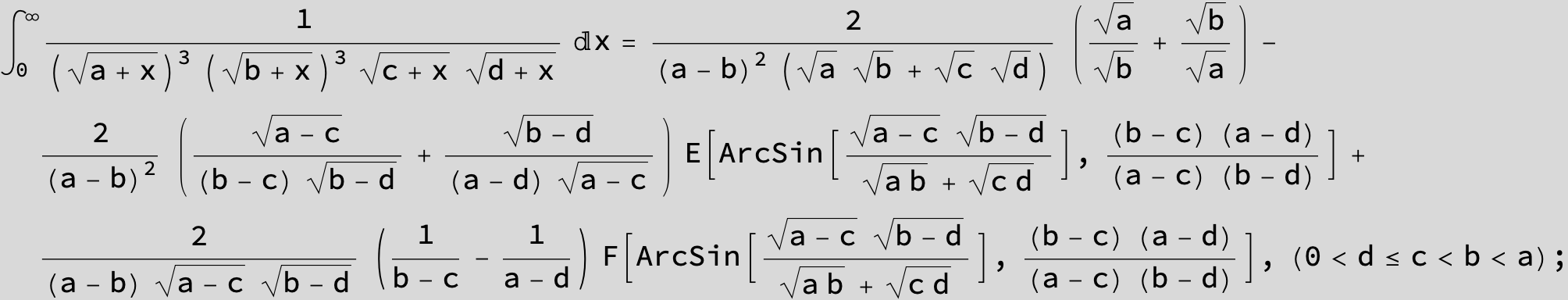
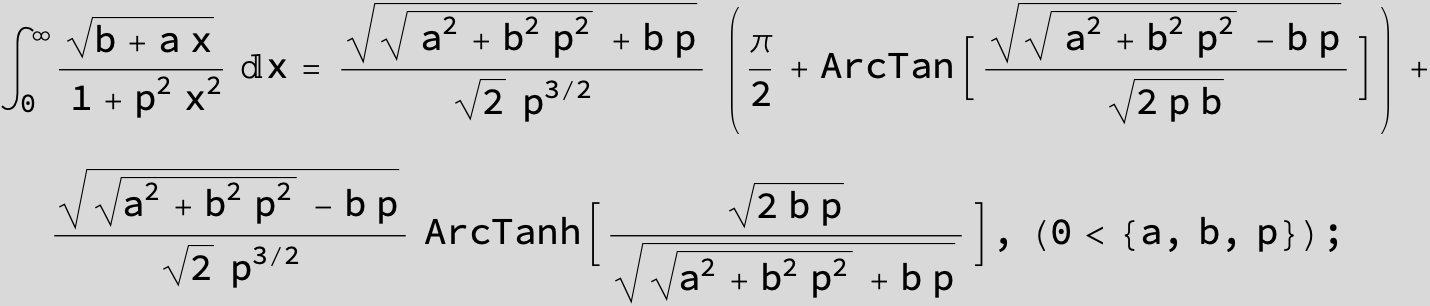
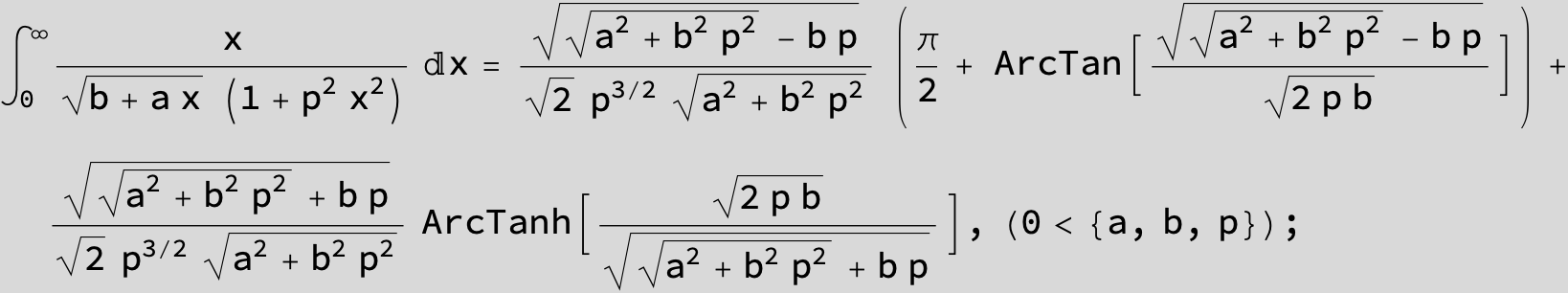
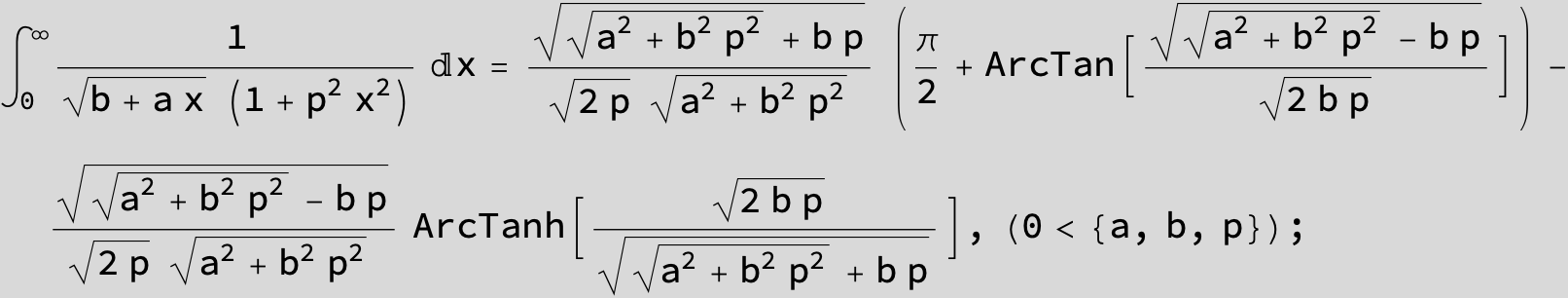
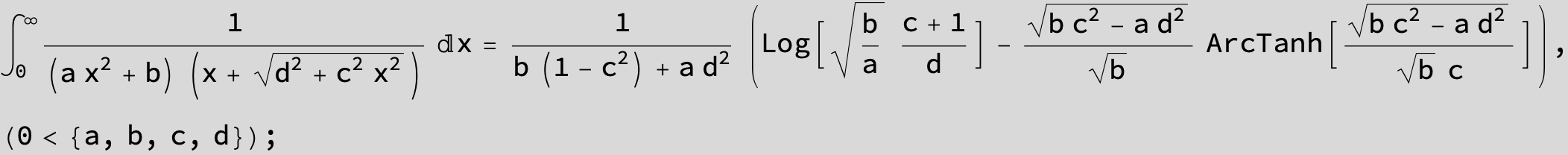
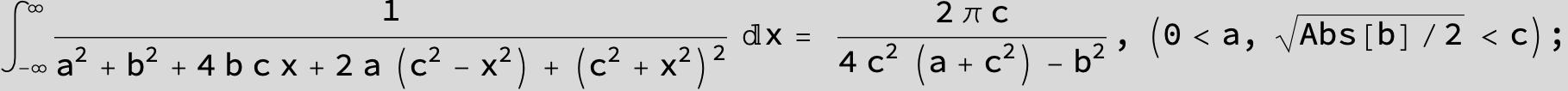
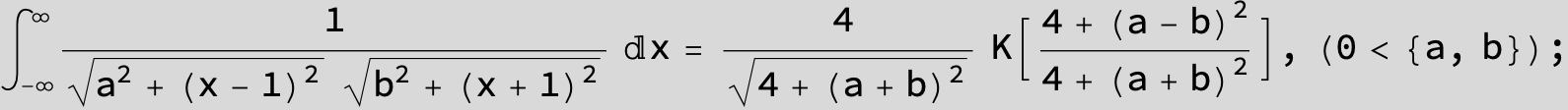
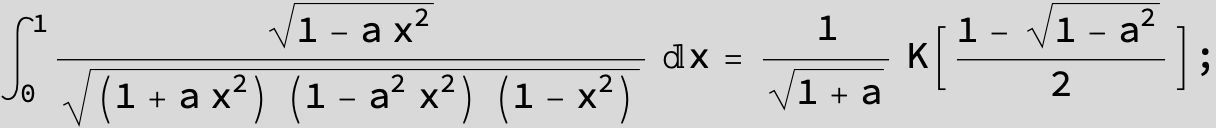
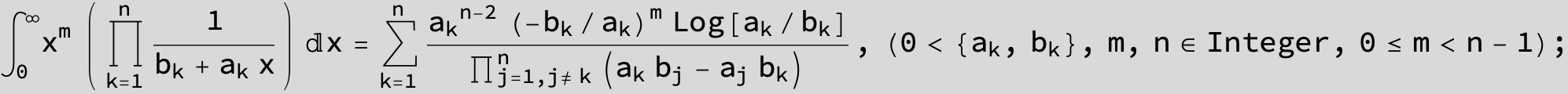
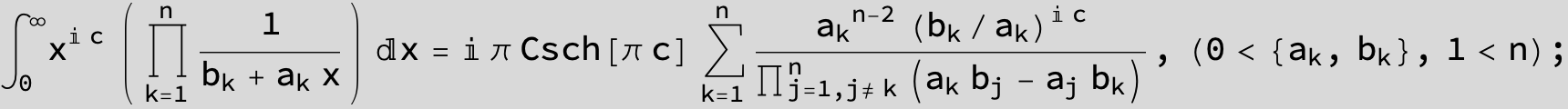
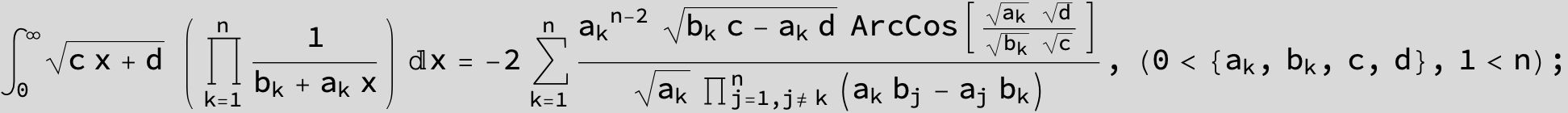
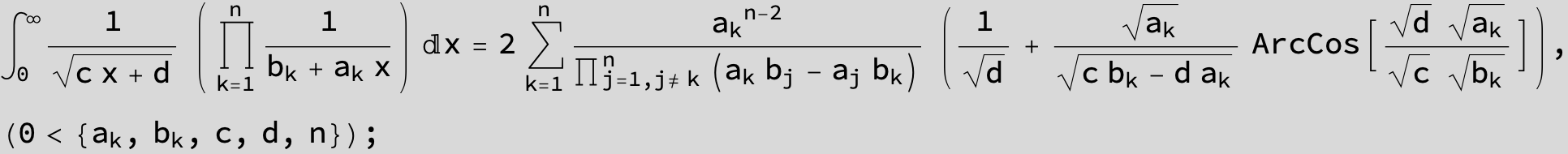
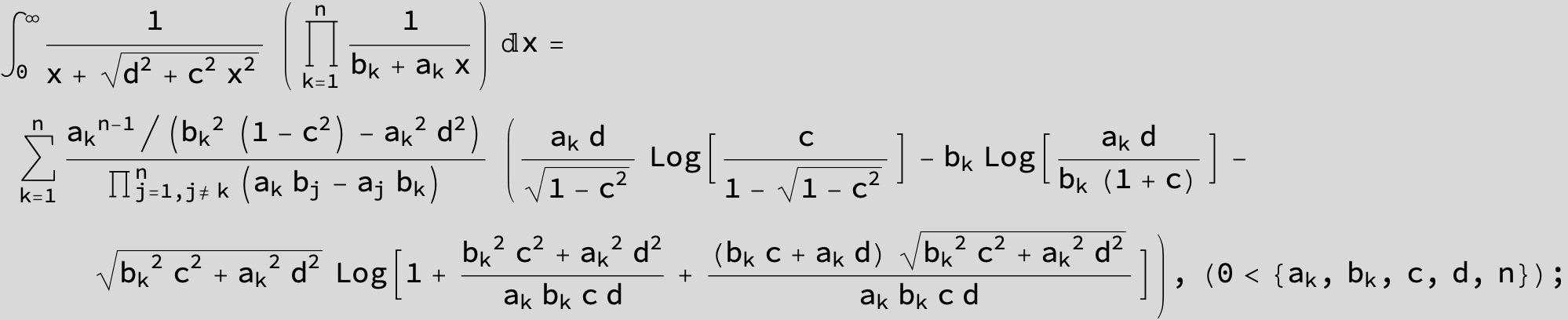
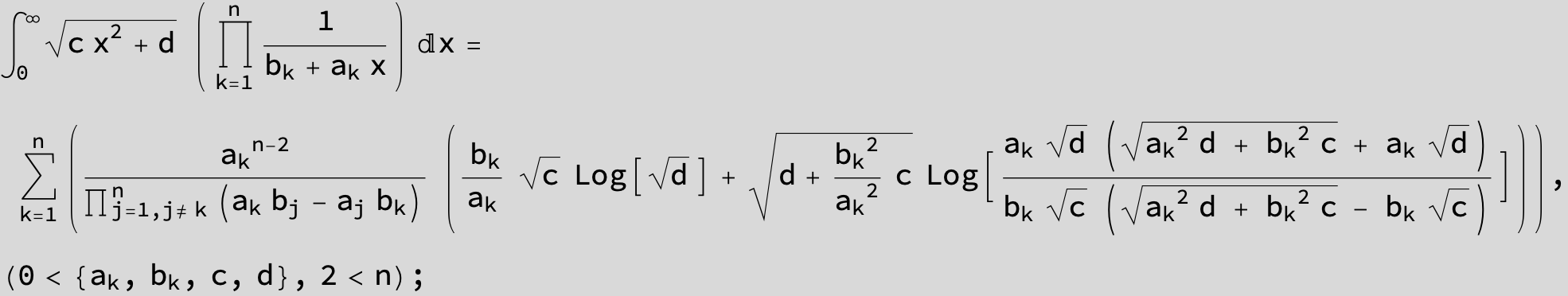
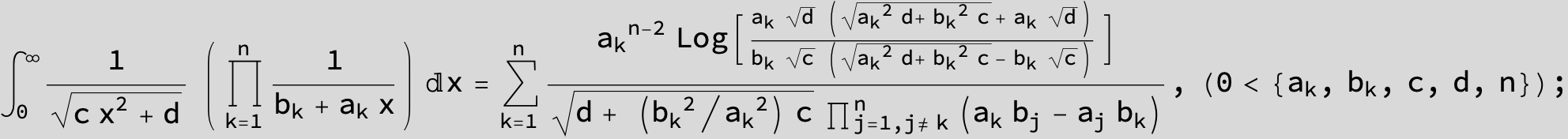
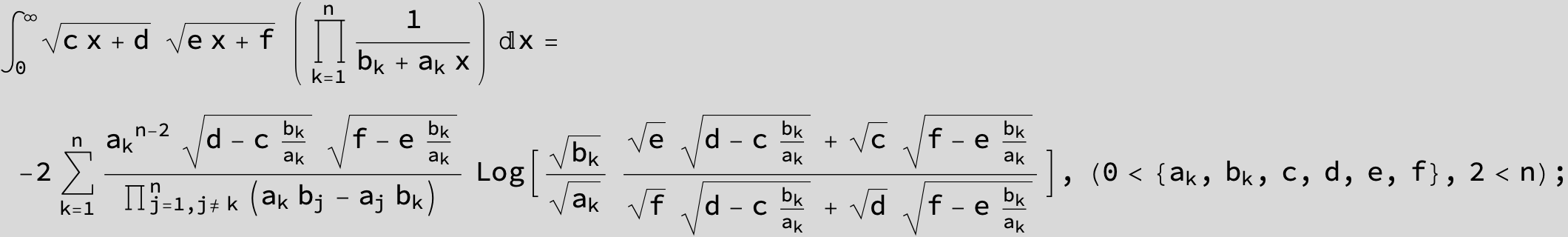
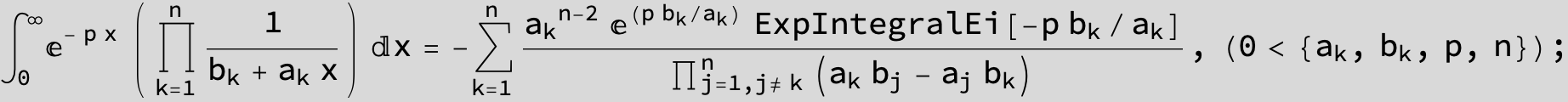
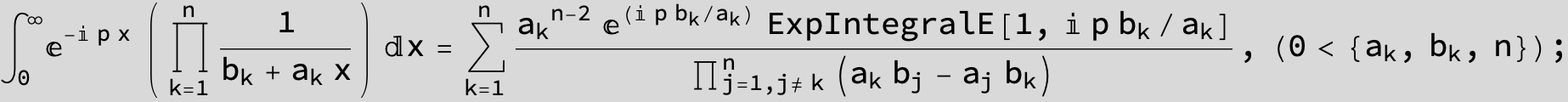
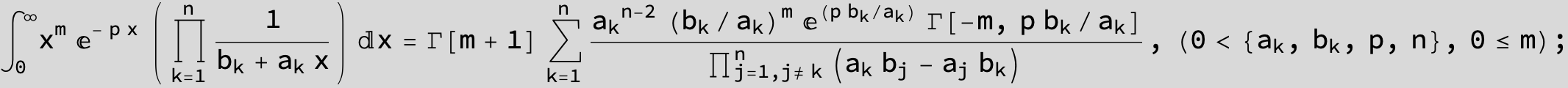
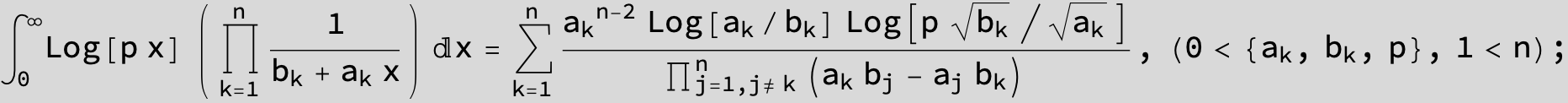
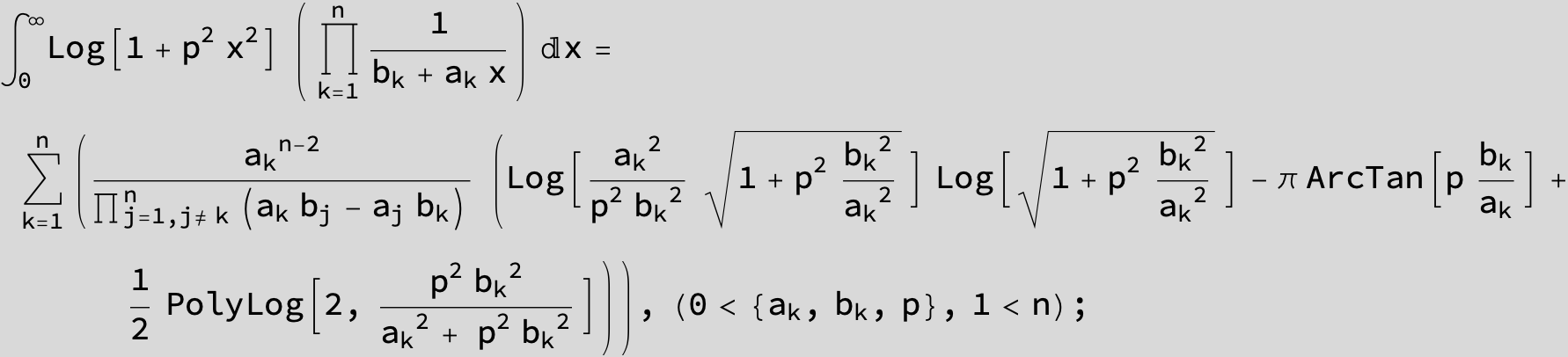
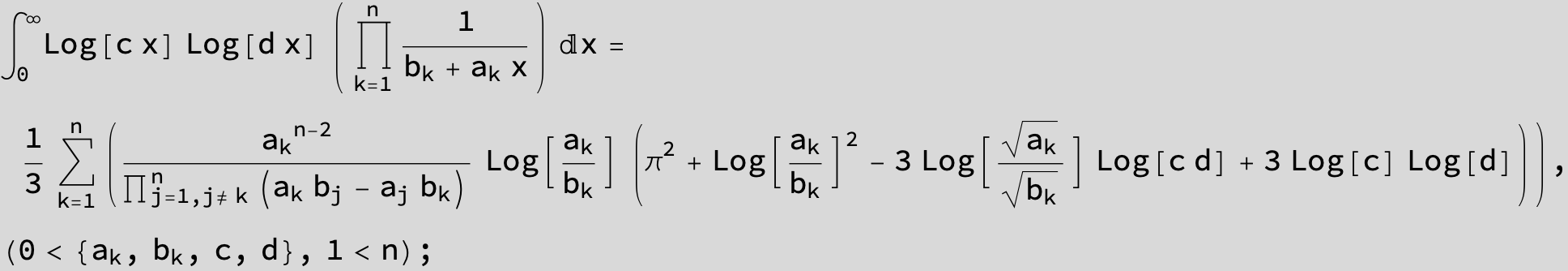
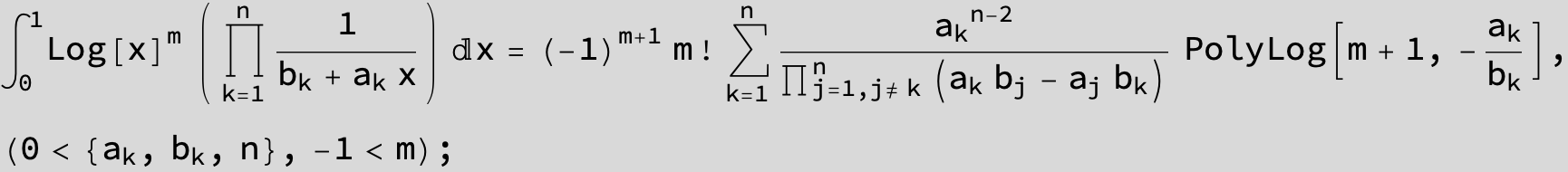
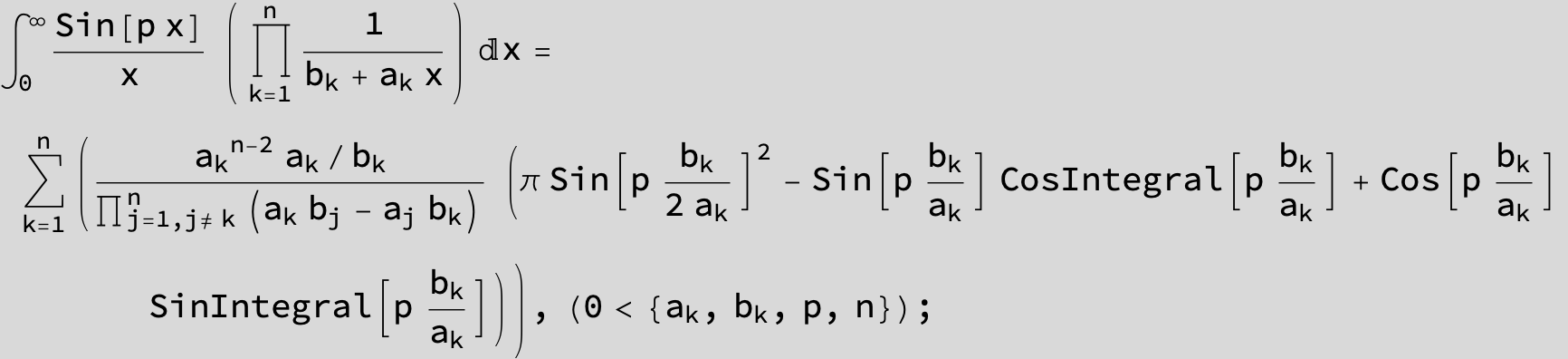
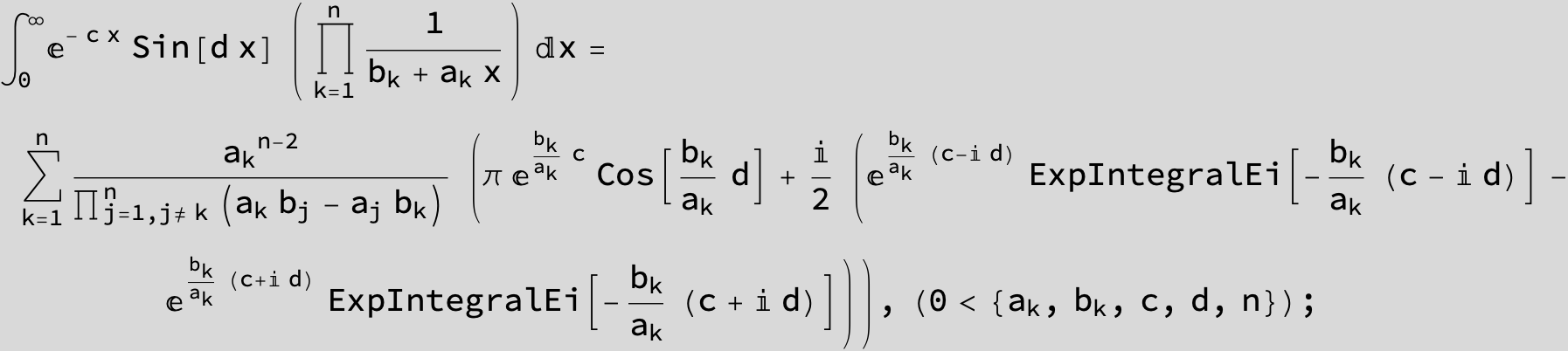
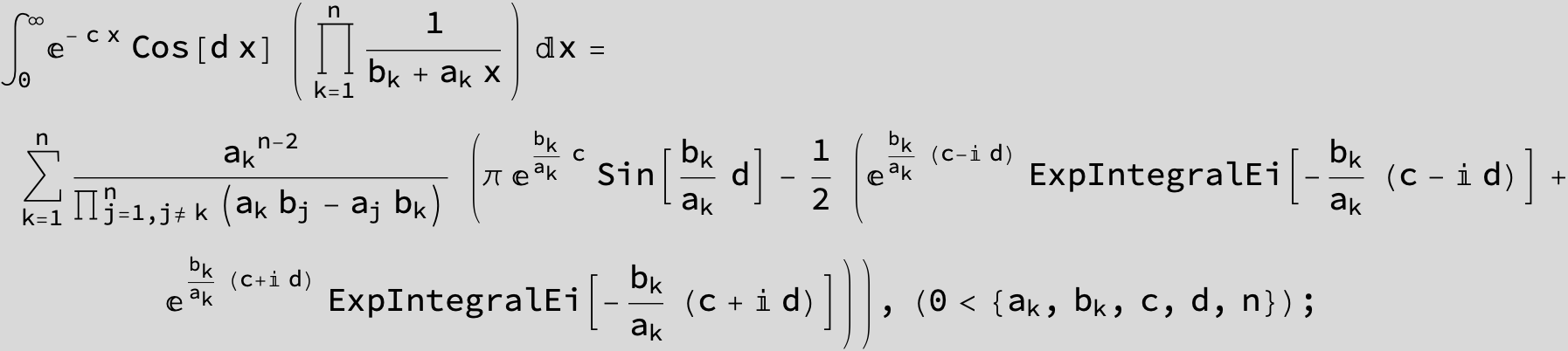
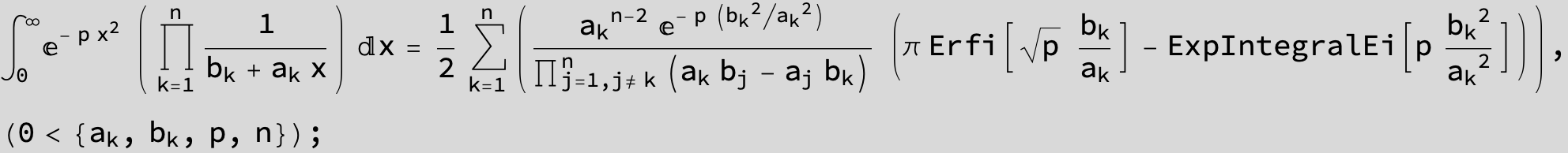
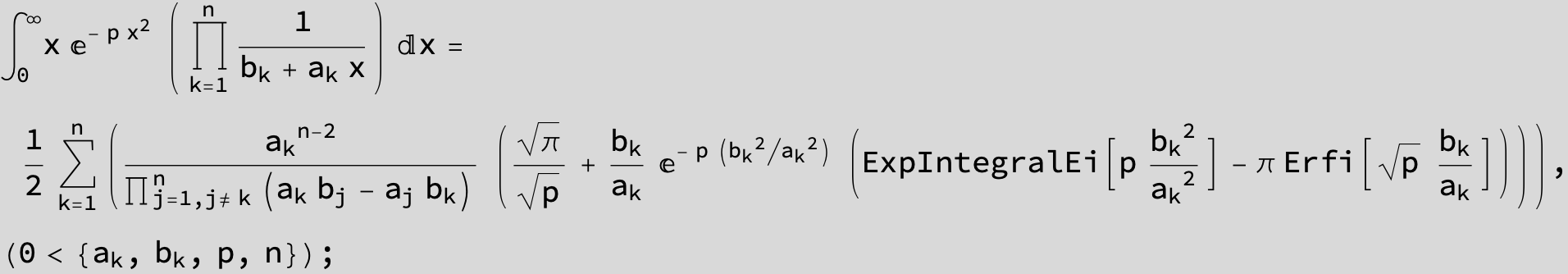
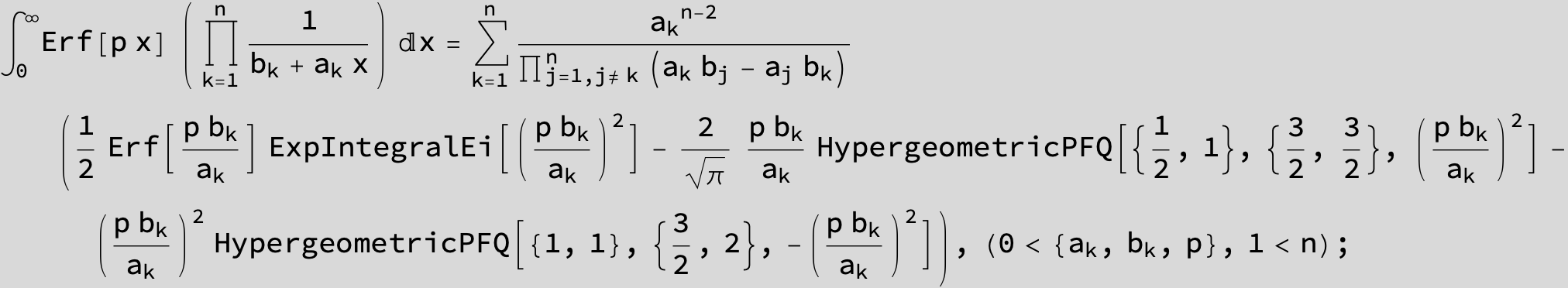
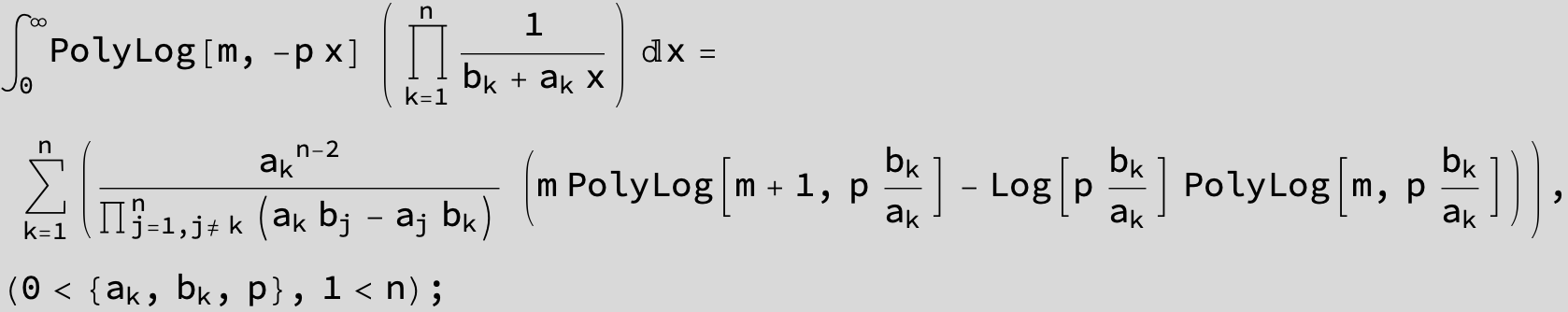
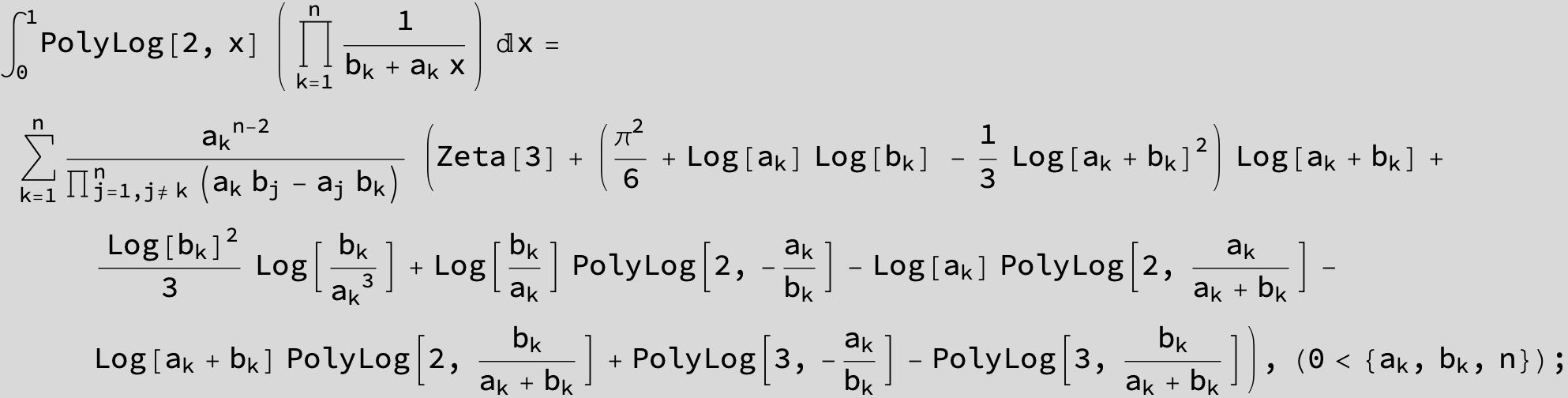
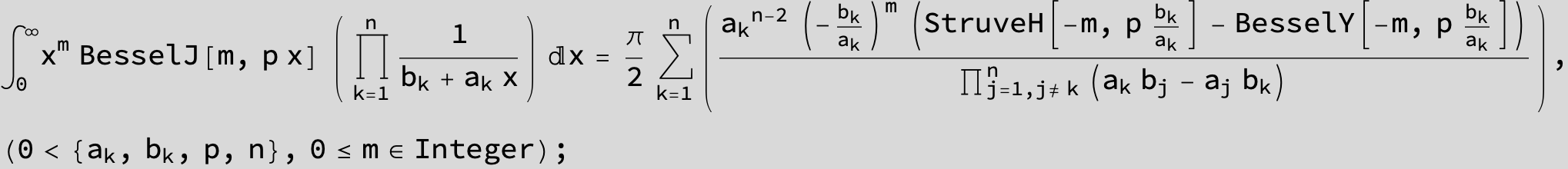
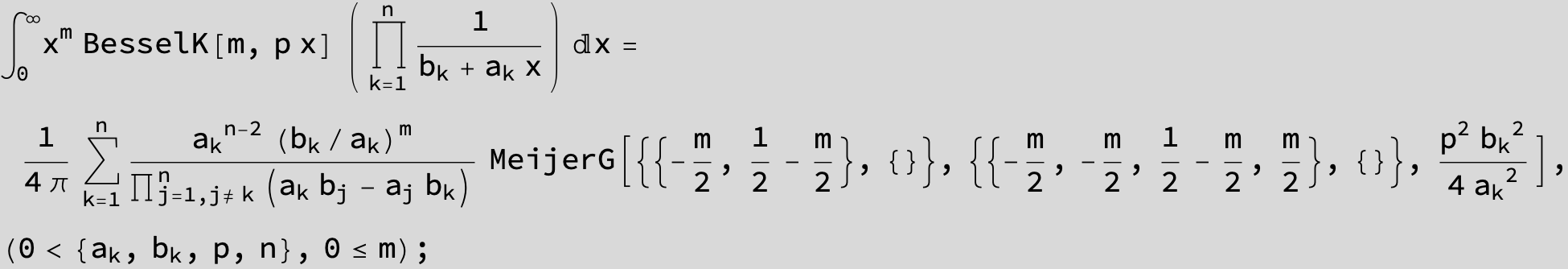
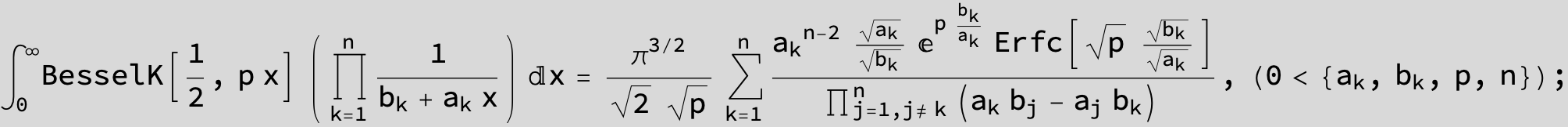
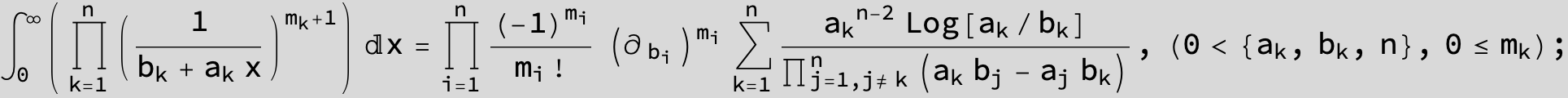
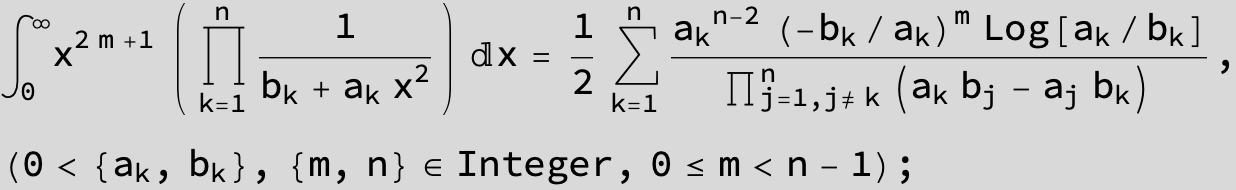
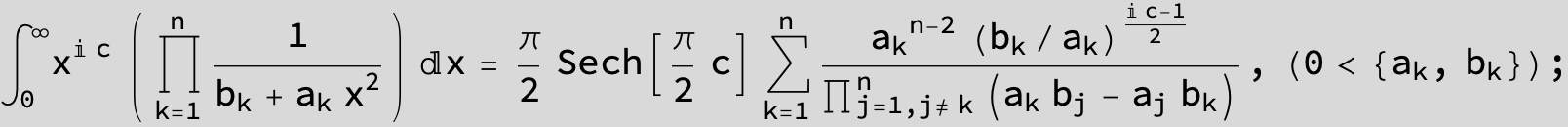
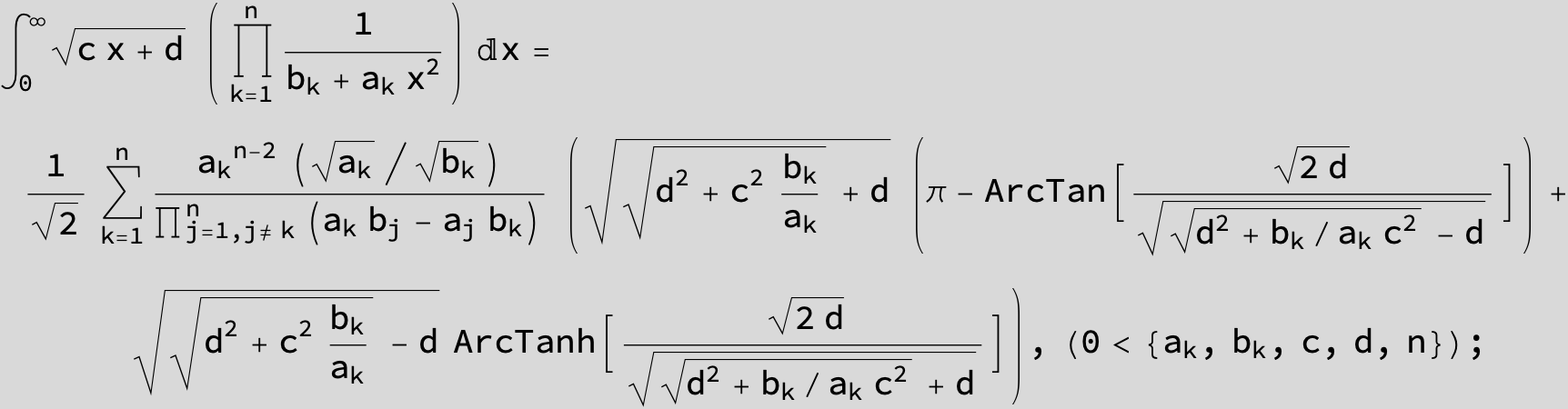
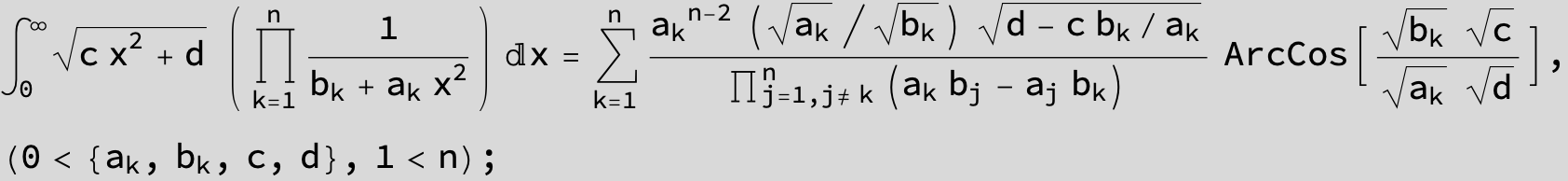
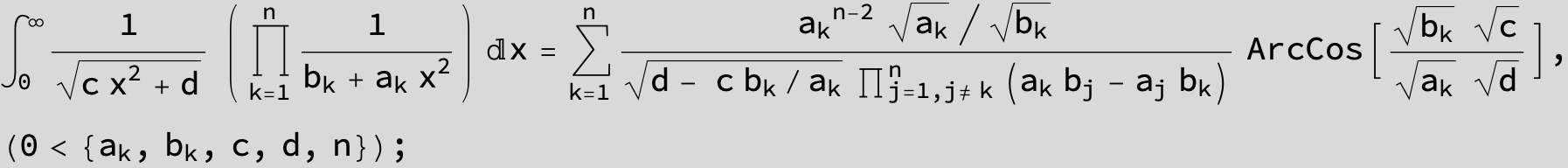
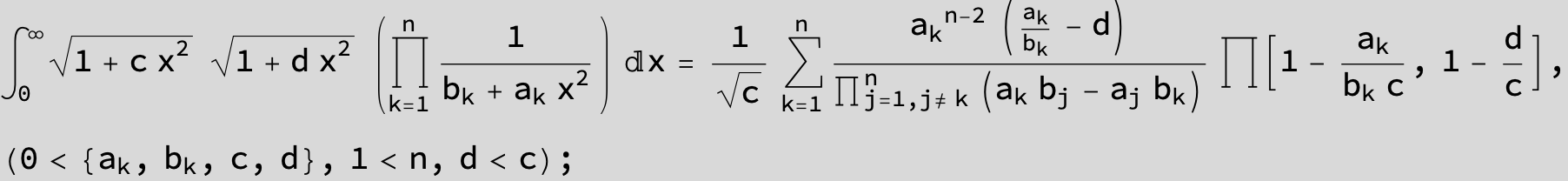
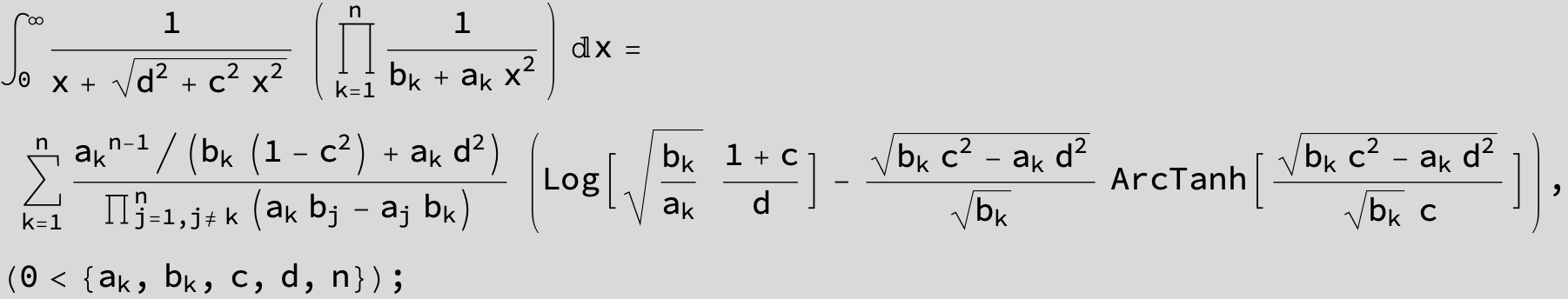
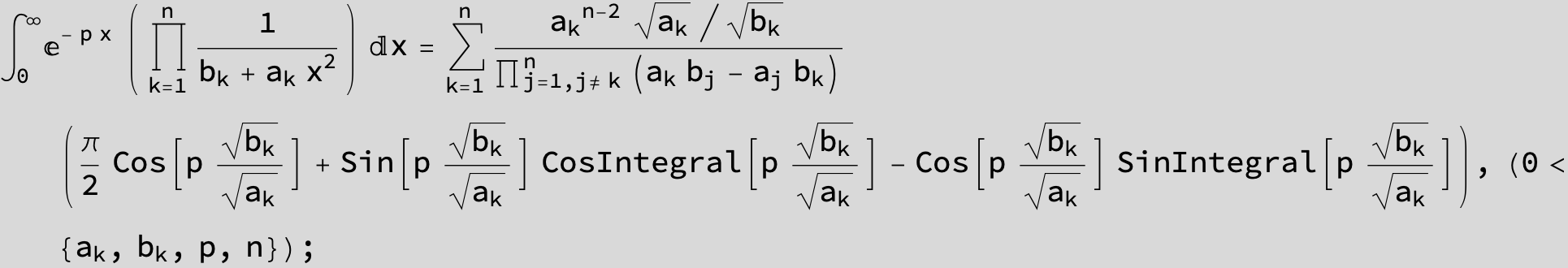
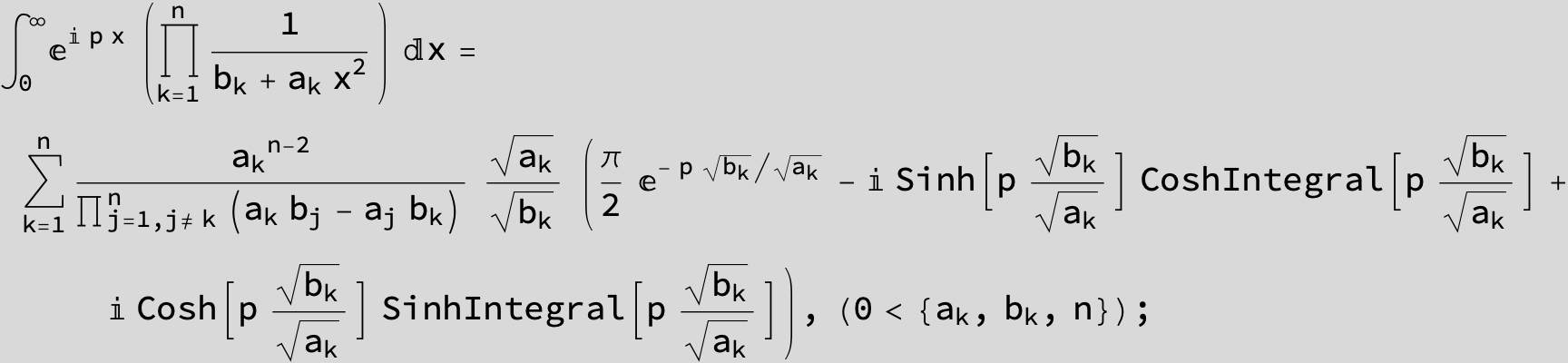
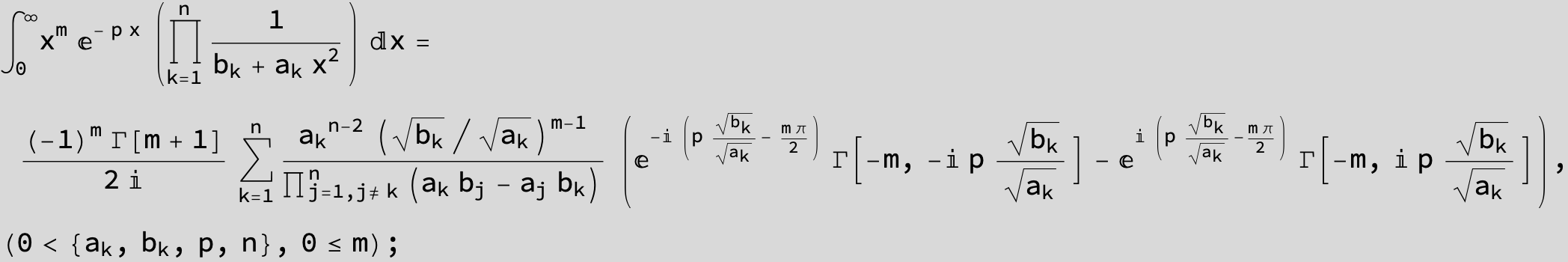
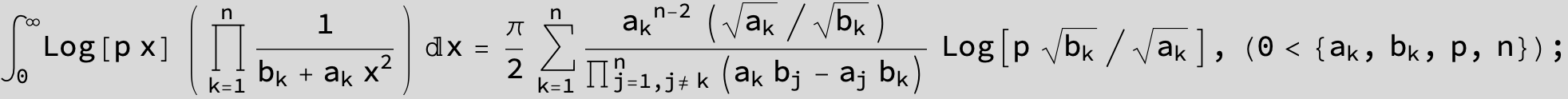
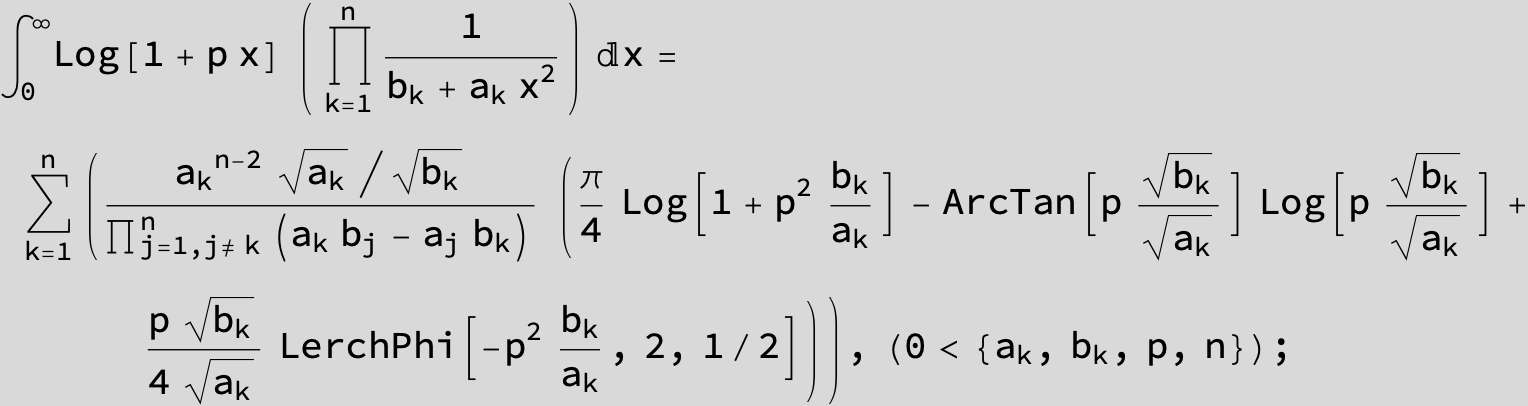
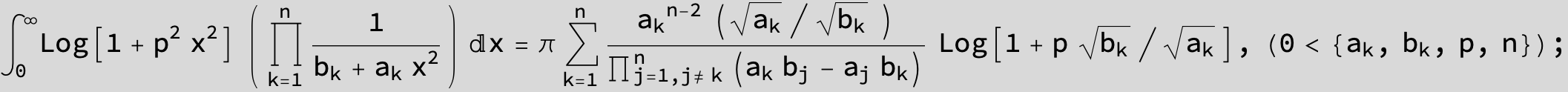
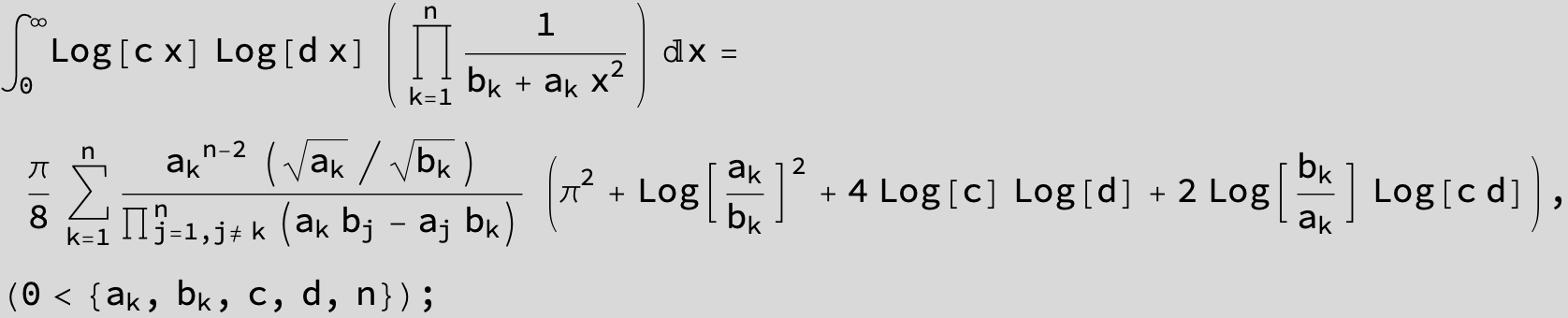
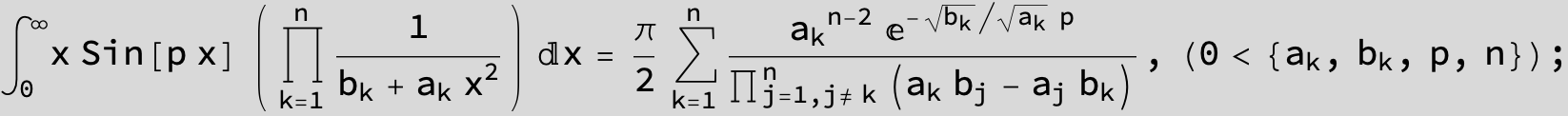
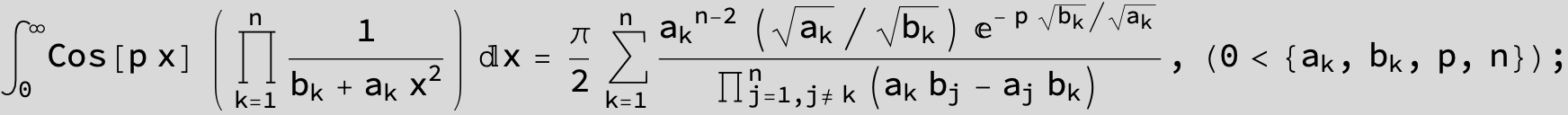
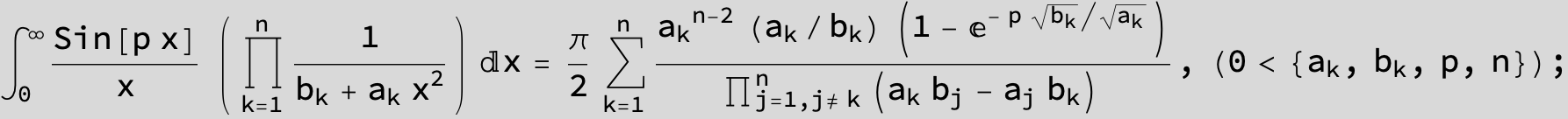
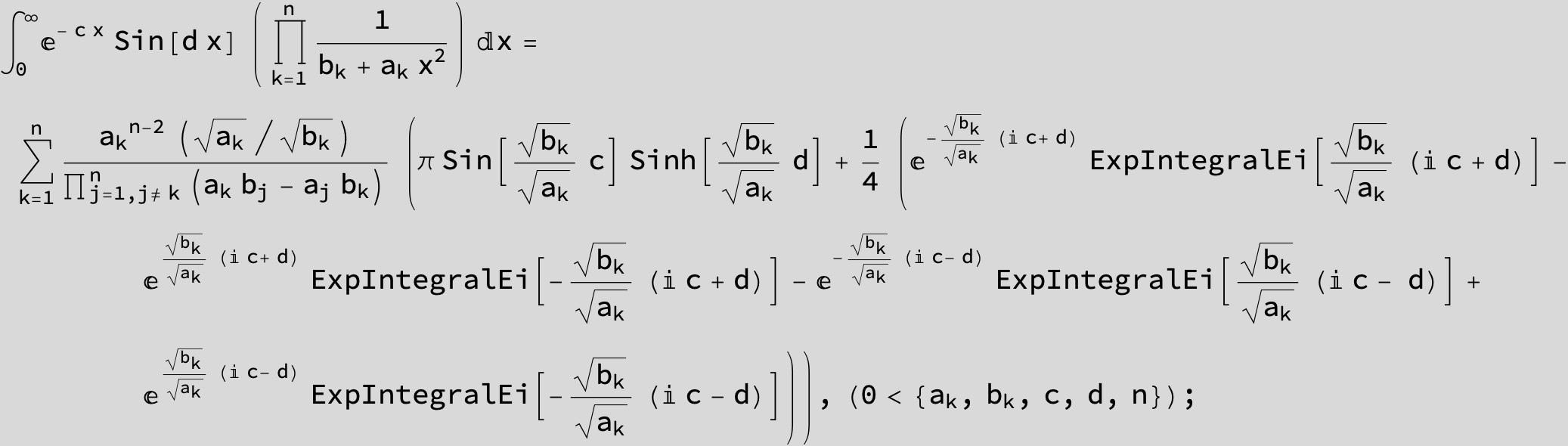
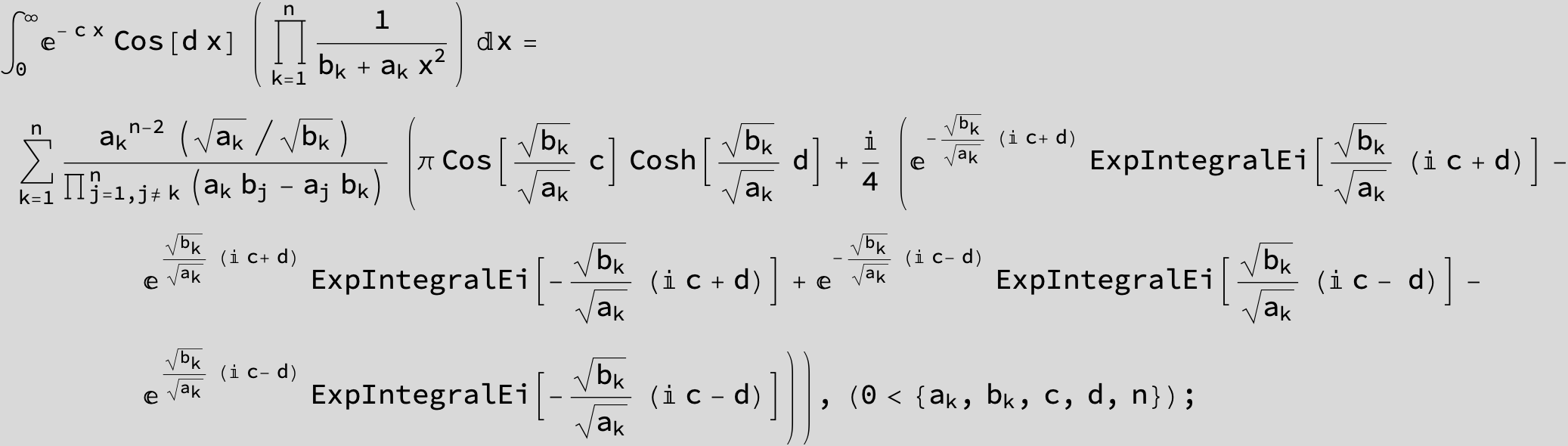
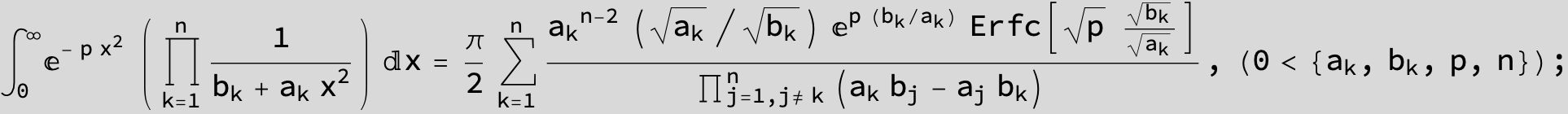
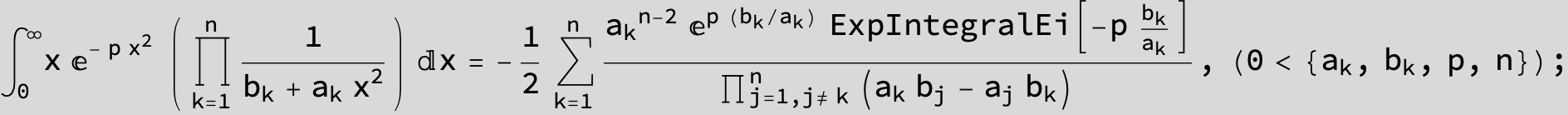
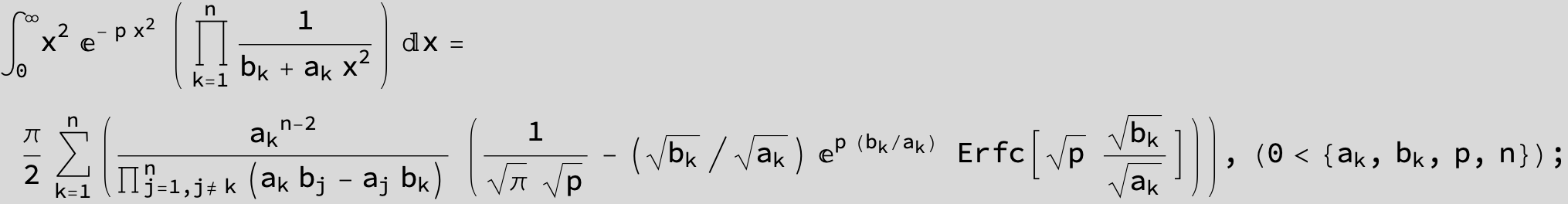
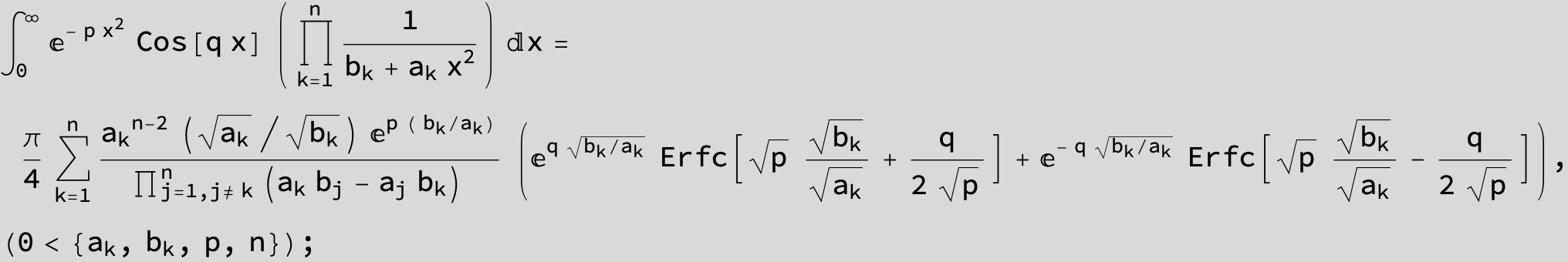
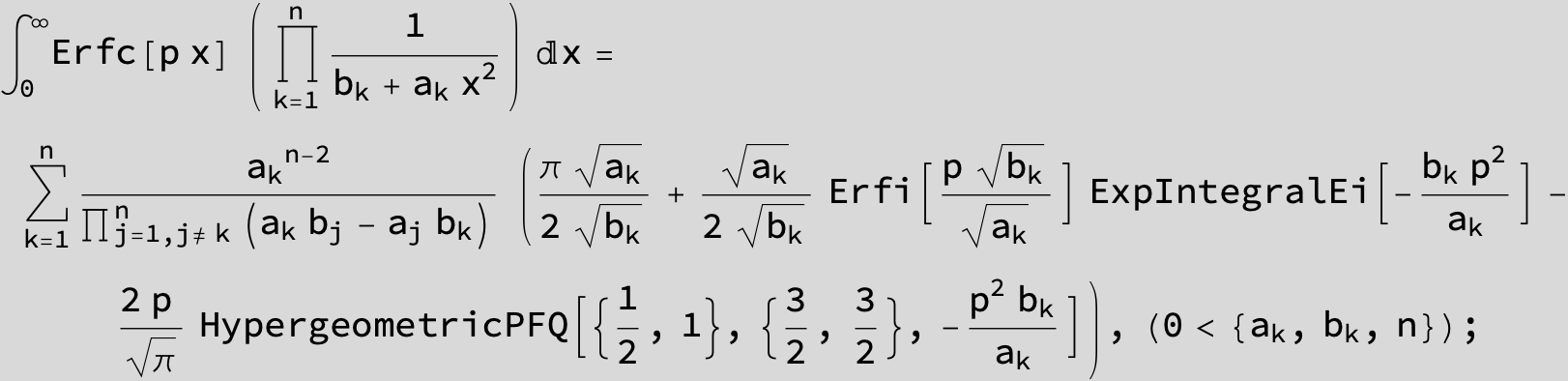
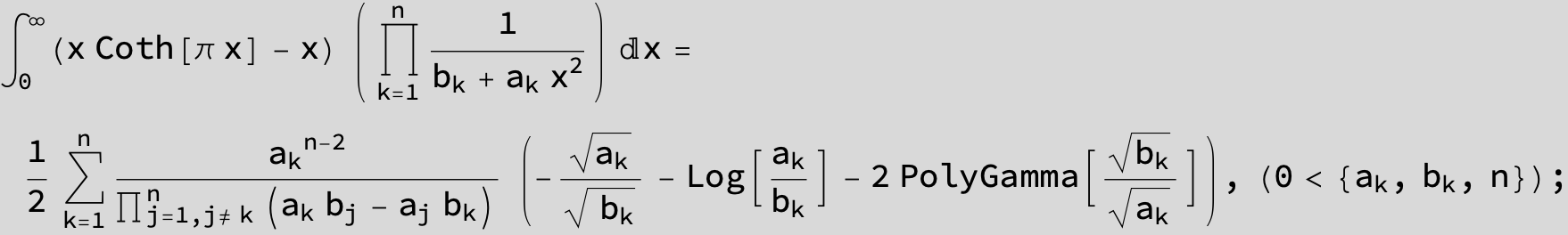
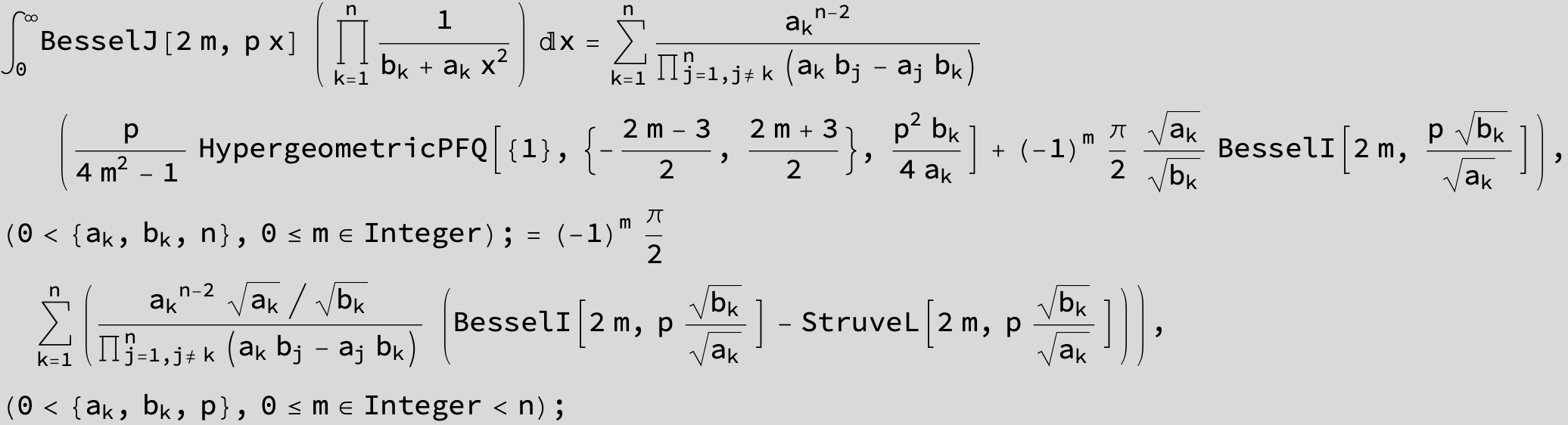
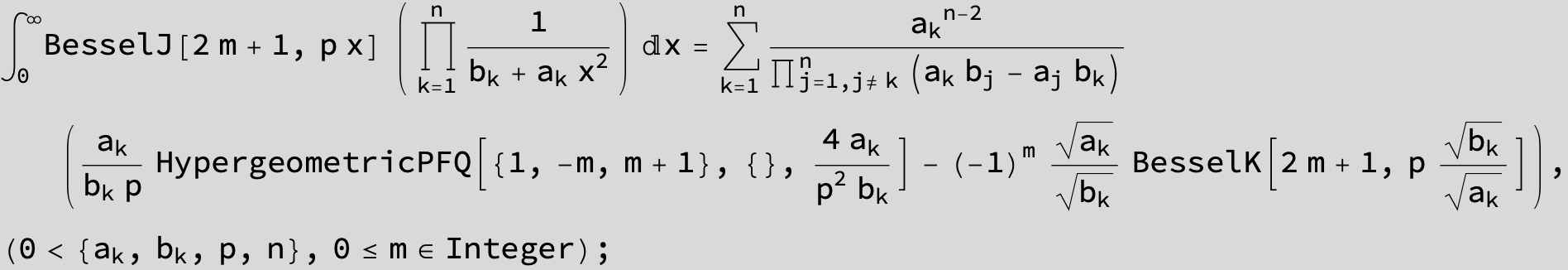
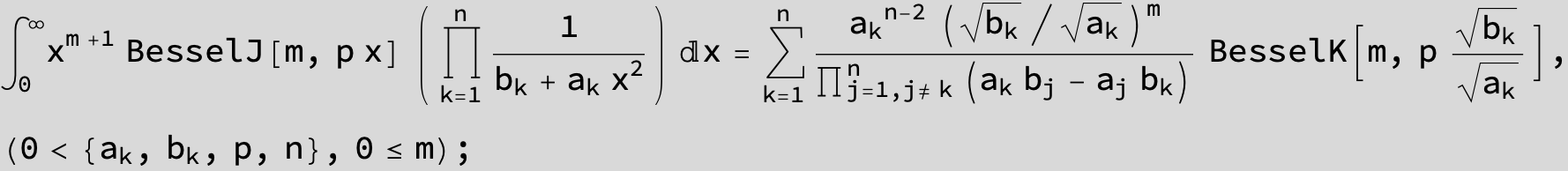
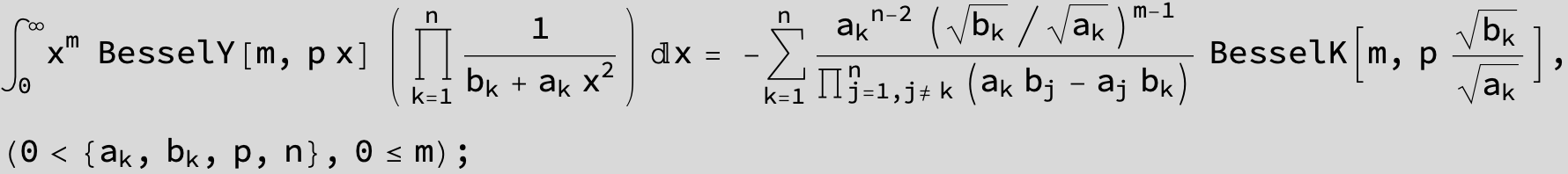
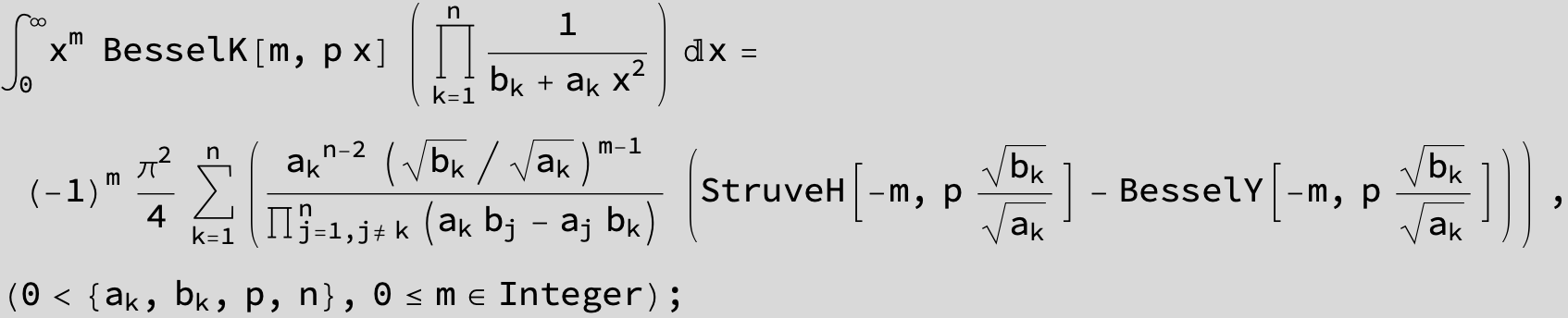
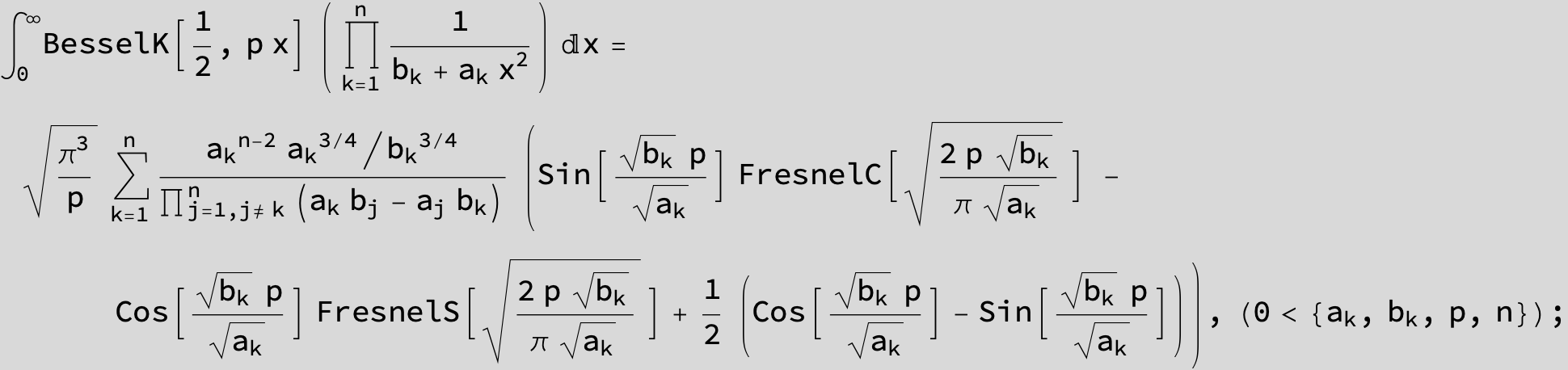
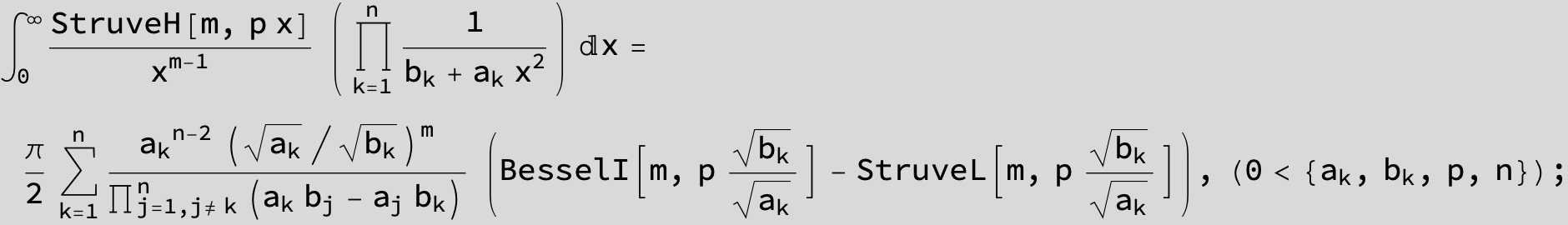
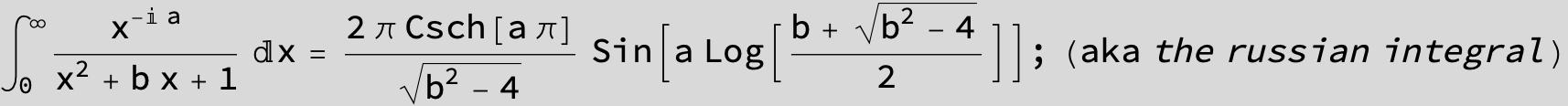
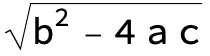
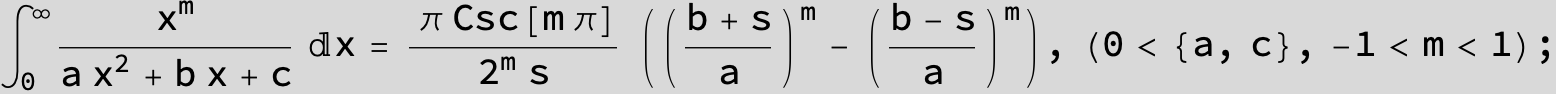
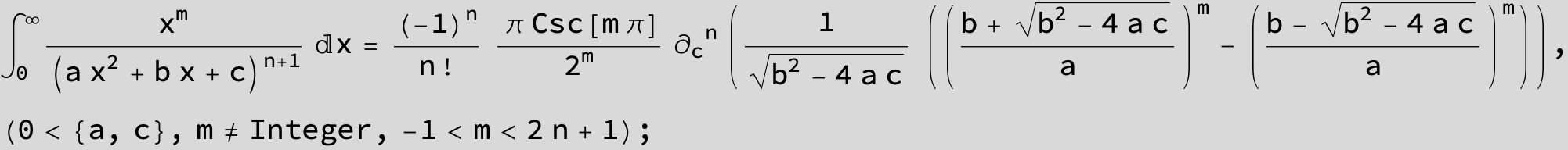
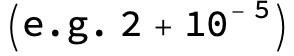
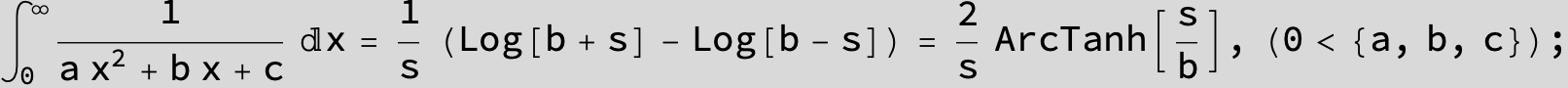
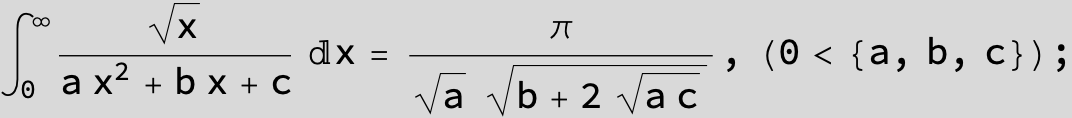
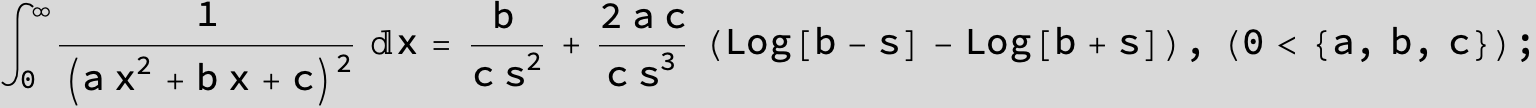
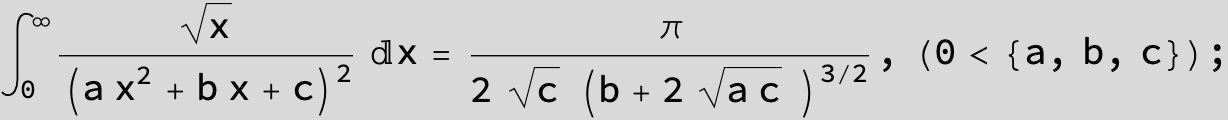
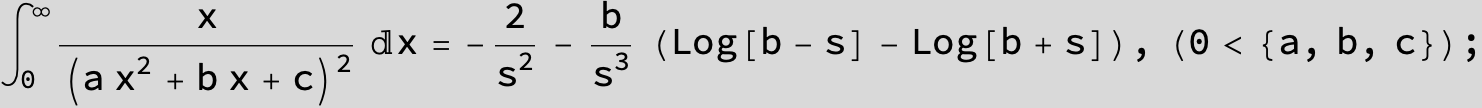
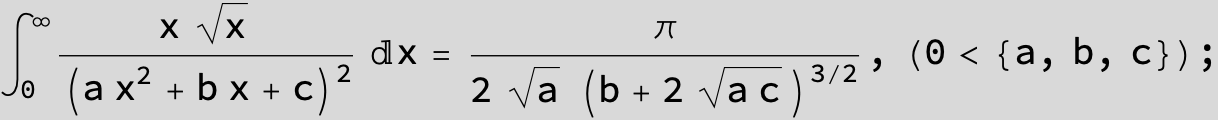
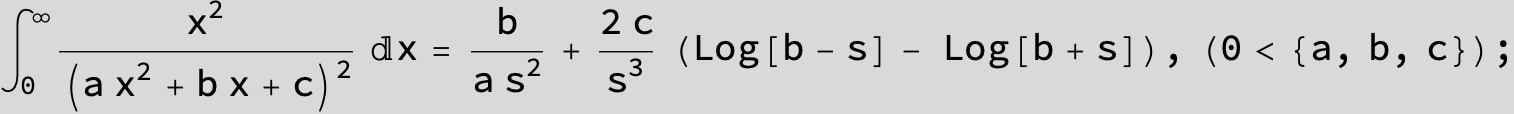
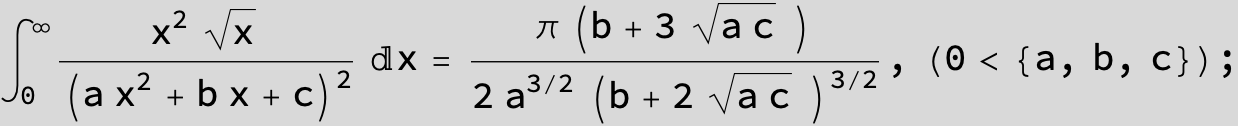
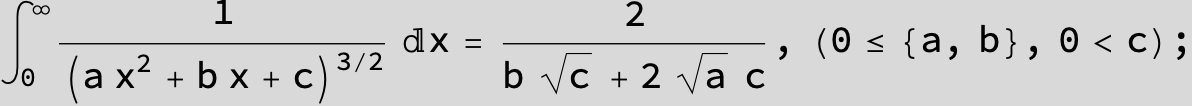
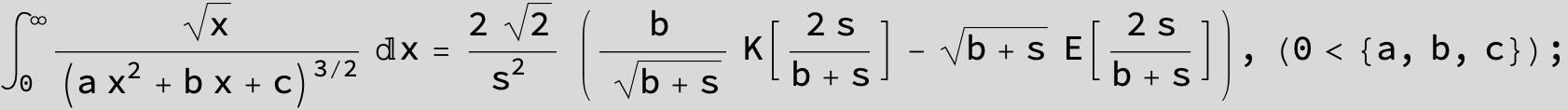
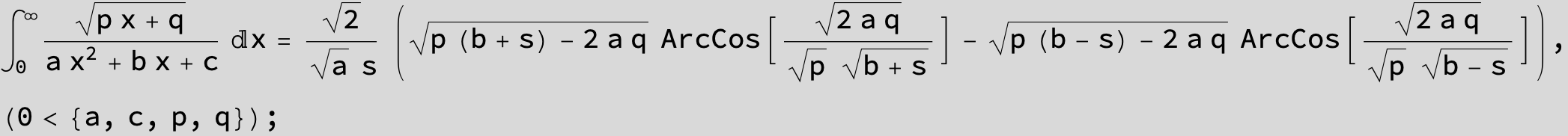
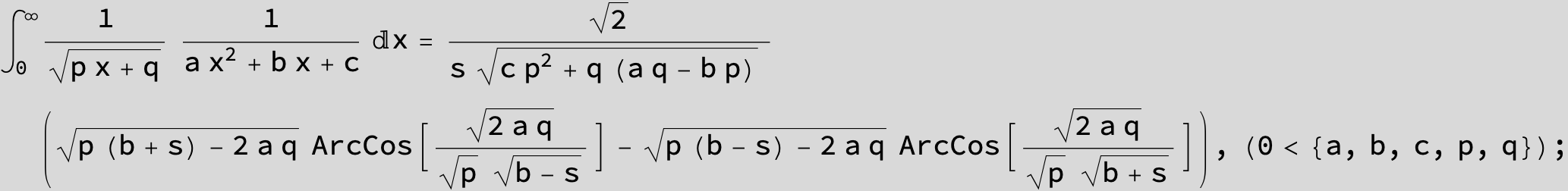
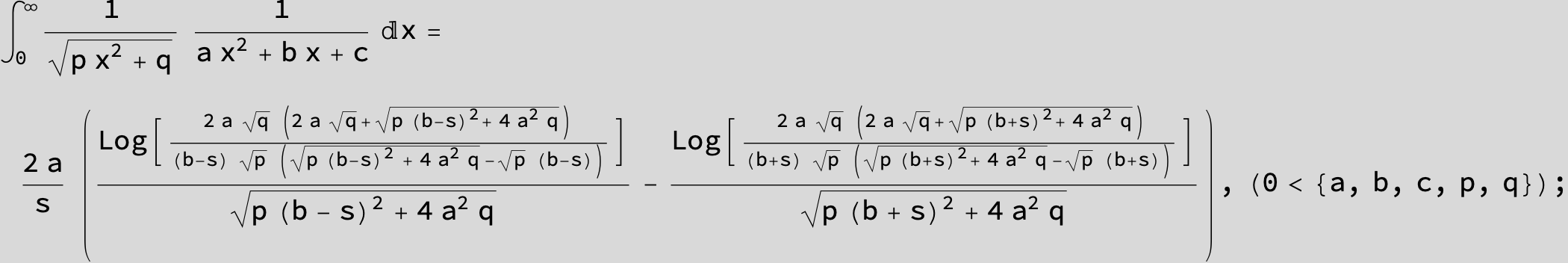
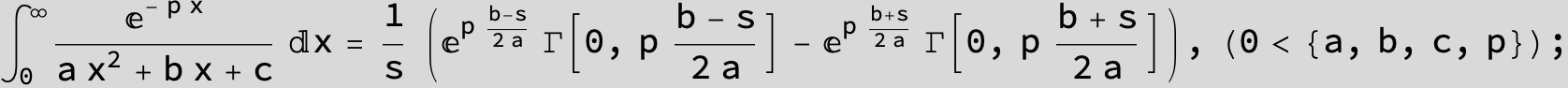
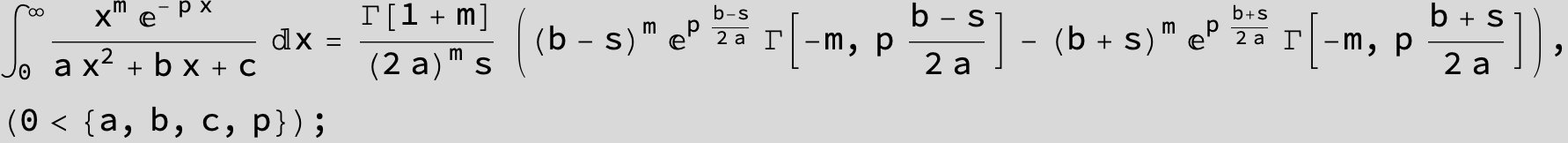
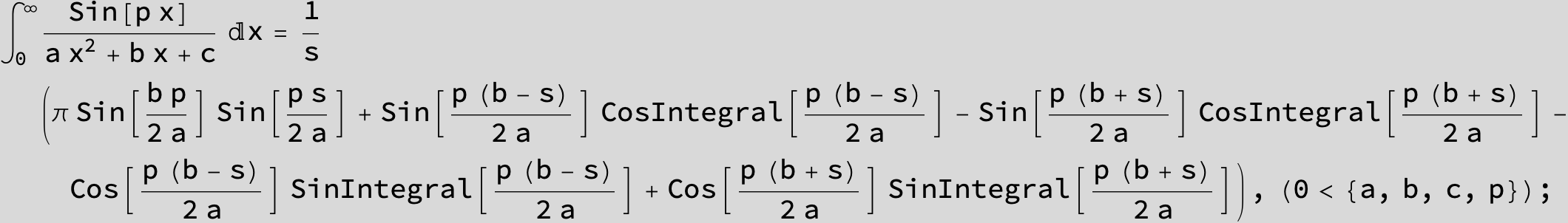
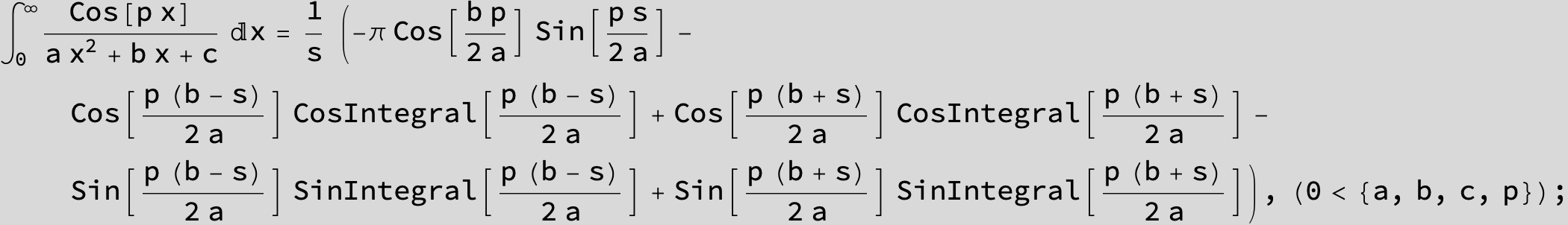
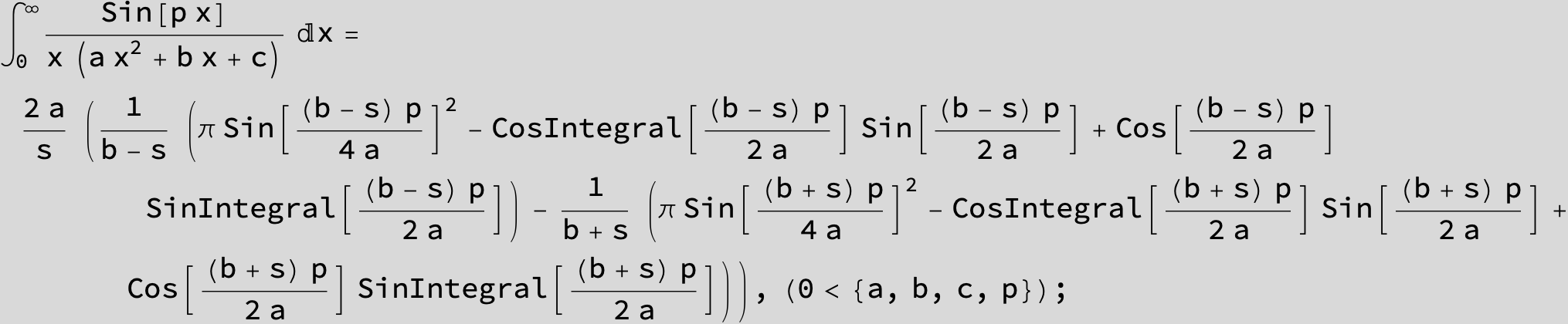
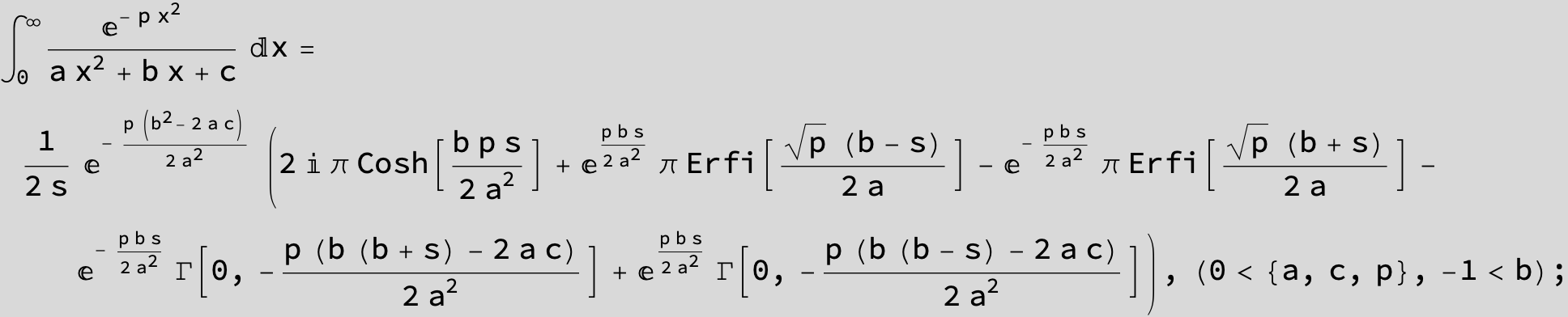
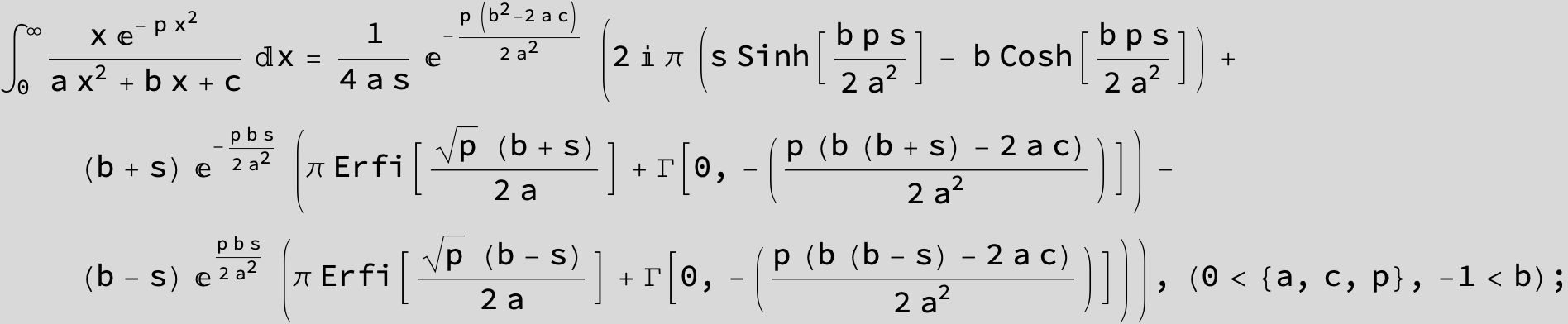
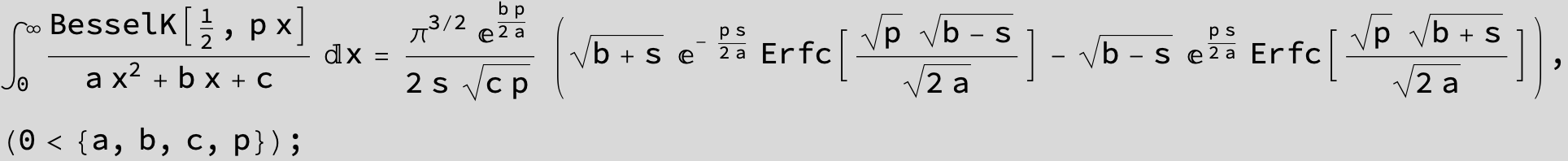
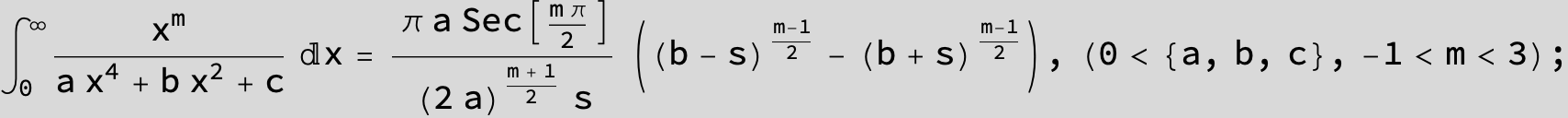
in the following expressions (∫ f(x)/(a x^2 + b x + c ) dx)   we abbreviate  s = :

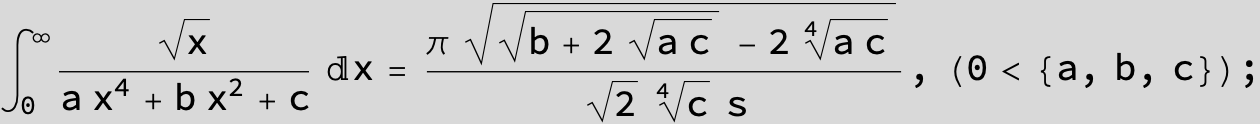
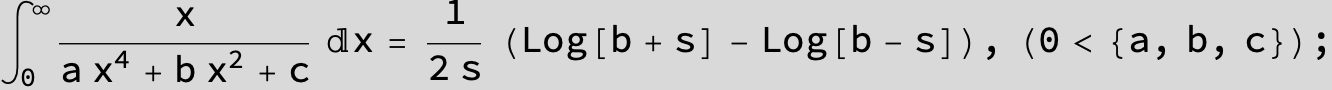
the values at integer n can be found approximately by setting n near to an integer .

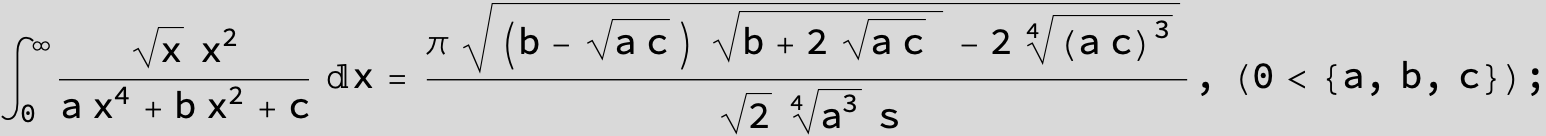
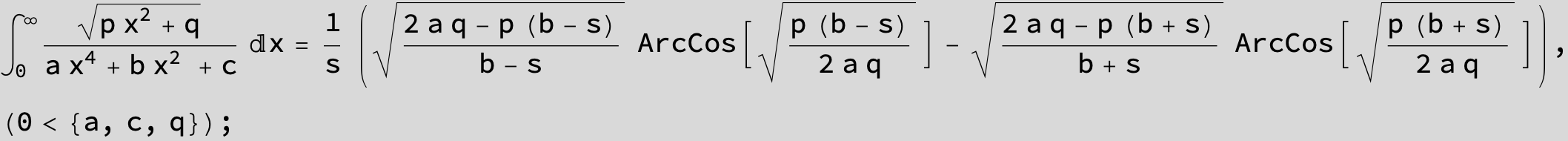
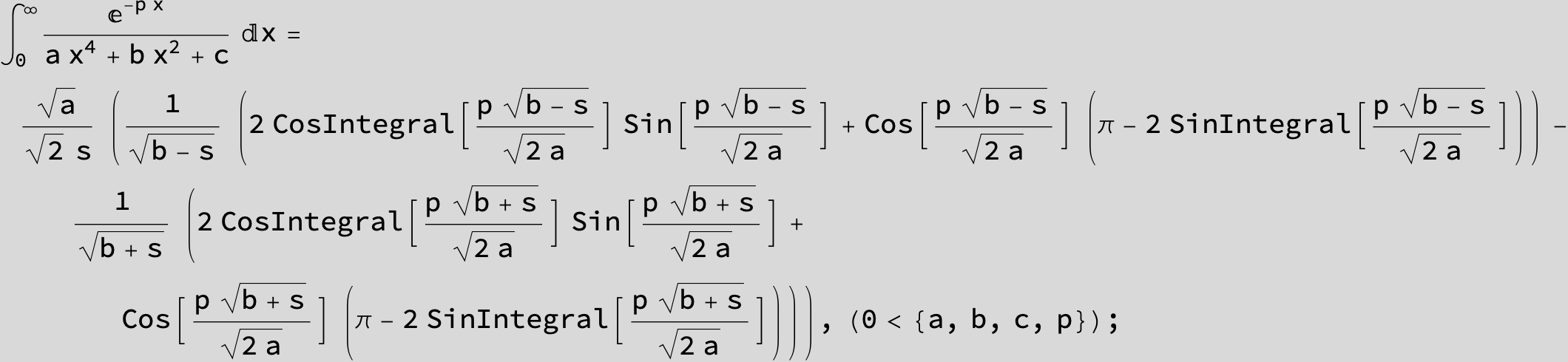
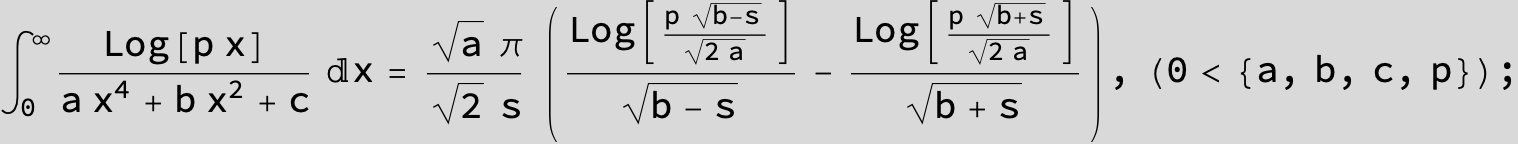
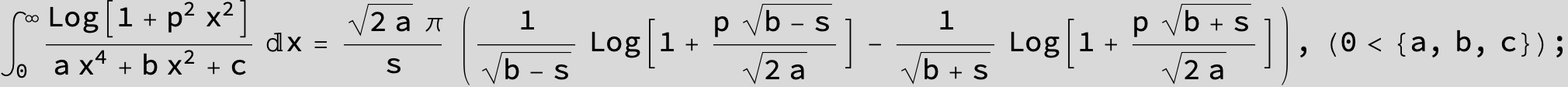
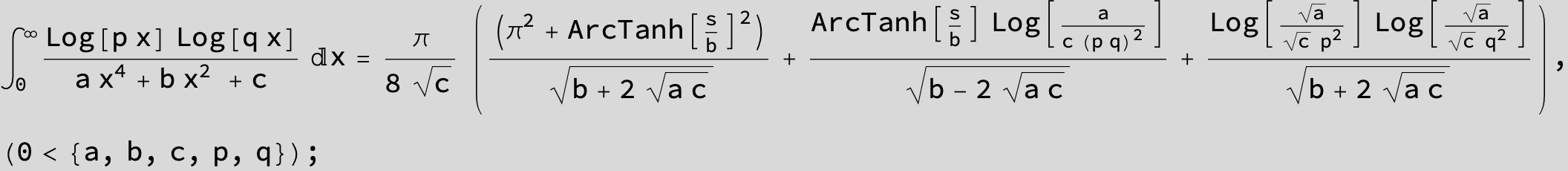
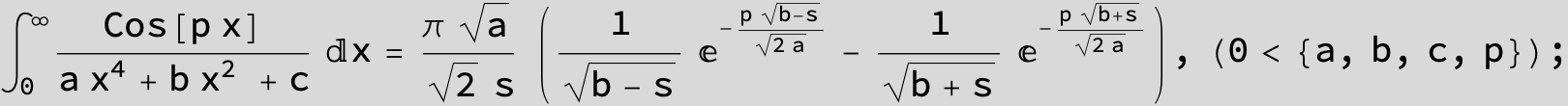
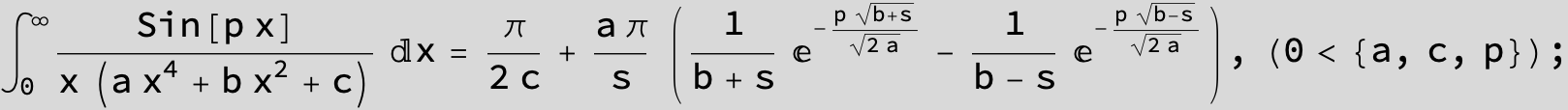
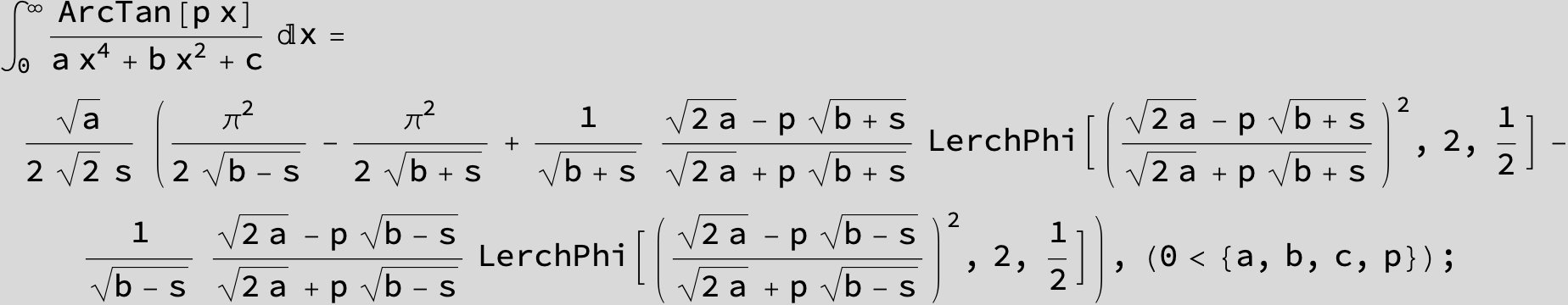
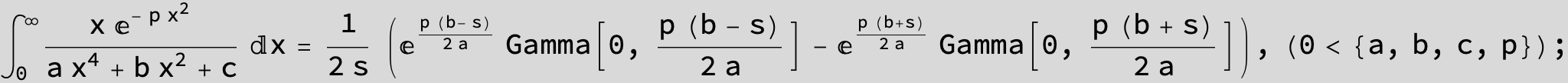
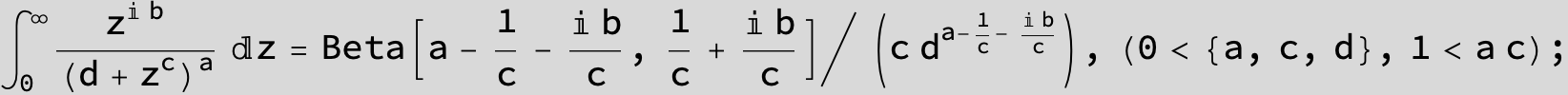
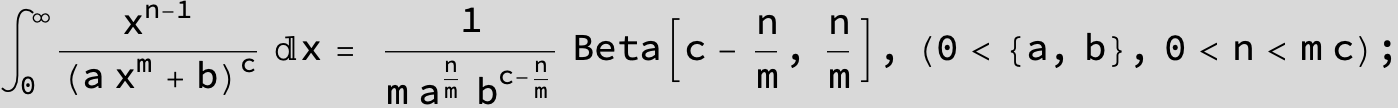
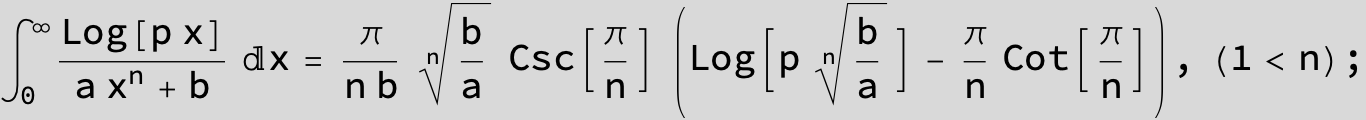
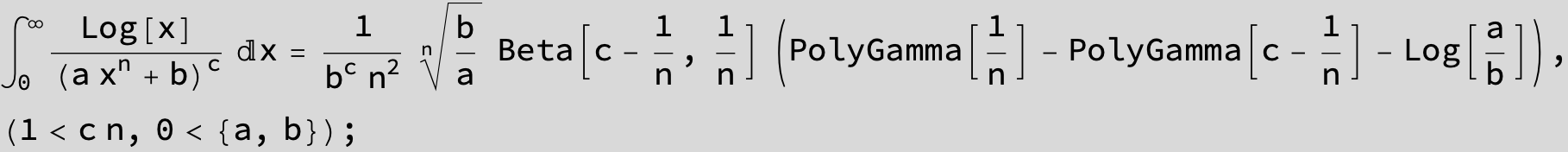
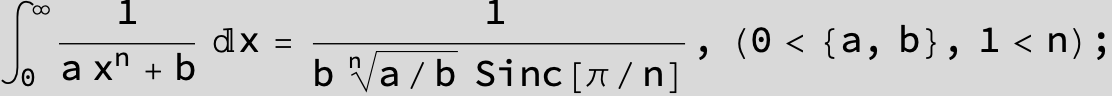
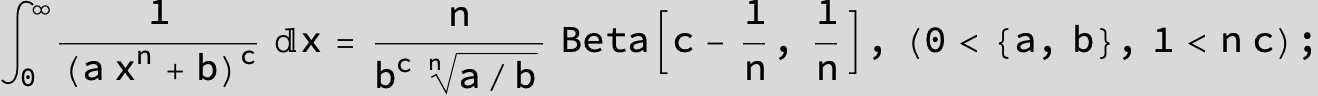
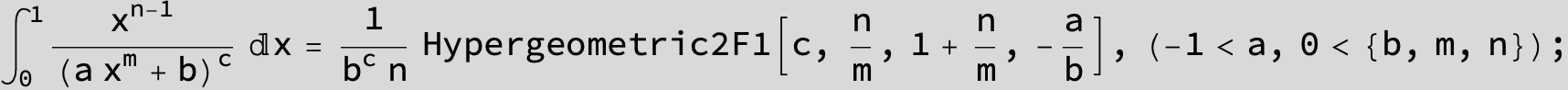
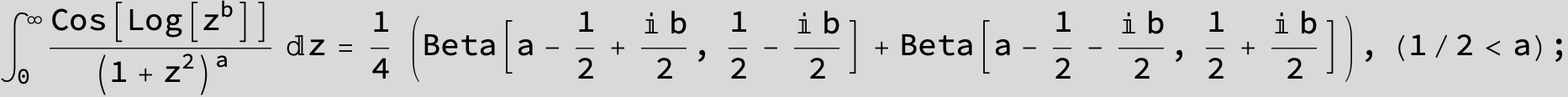
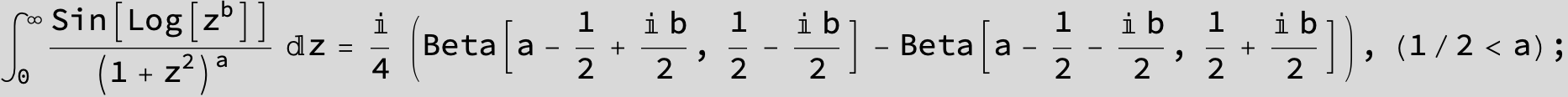
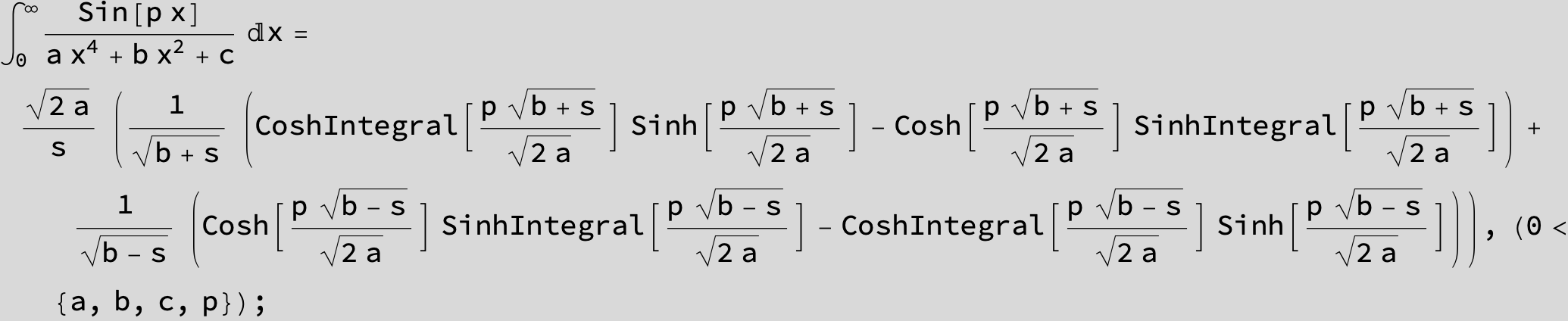
in the following expressions (∫ f(x)/(a x^4 + b x^2 + c ) dx)   we abbreviate s = :

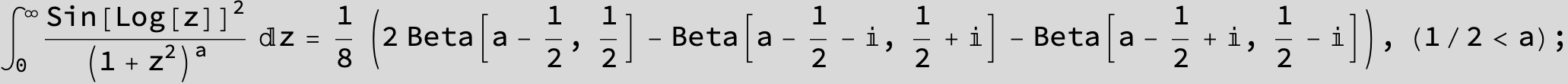
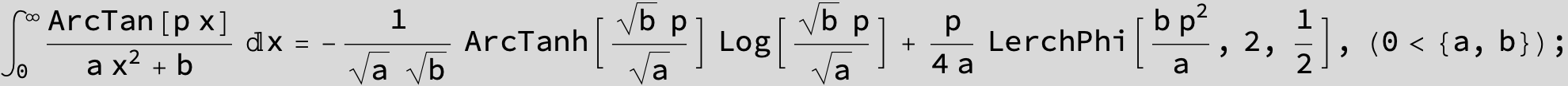
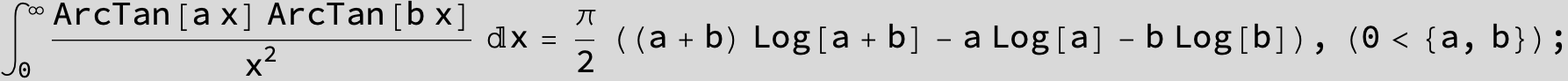
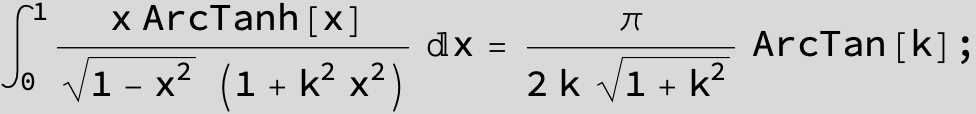
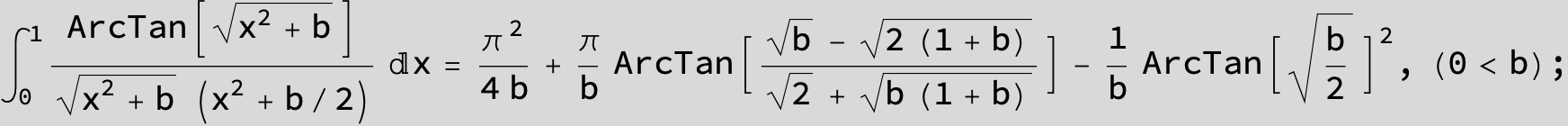
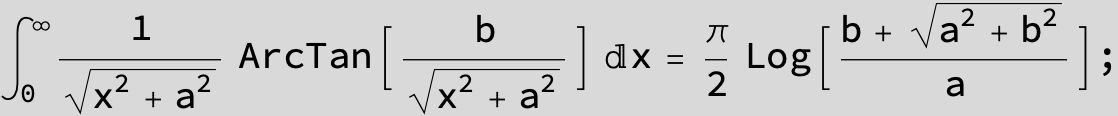
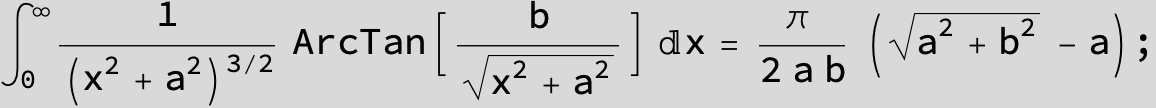
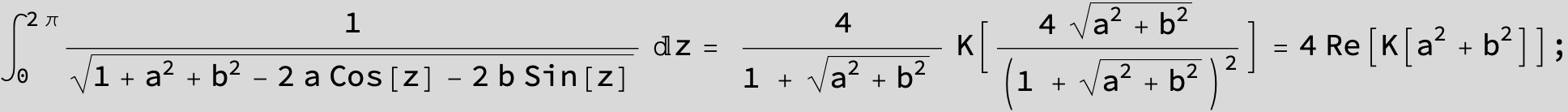
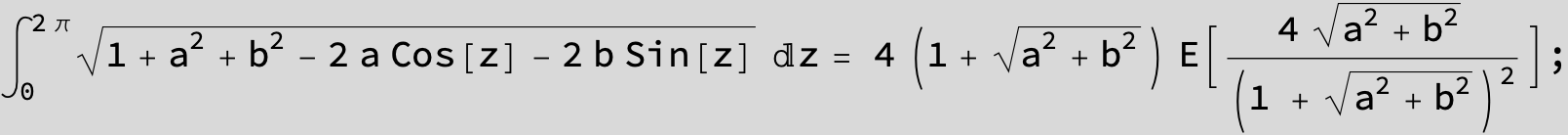
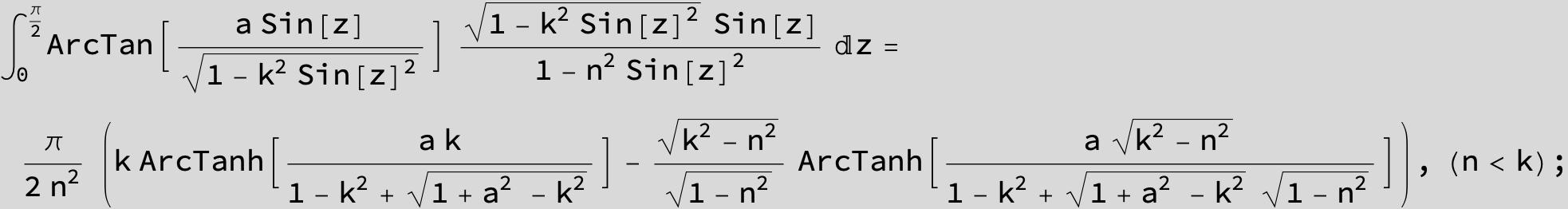
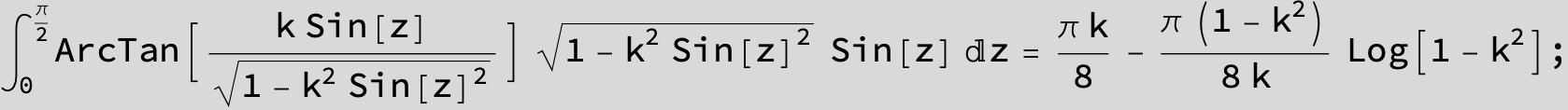
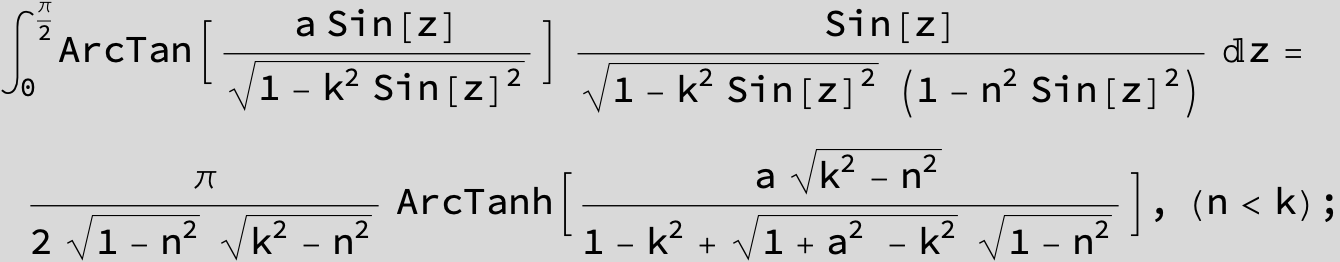
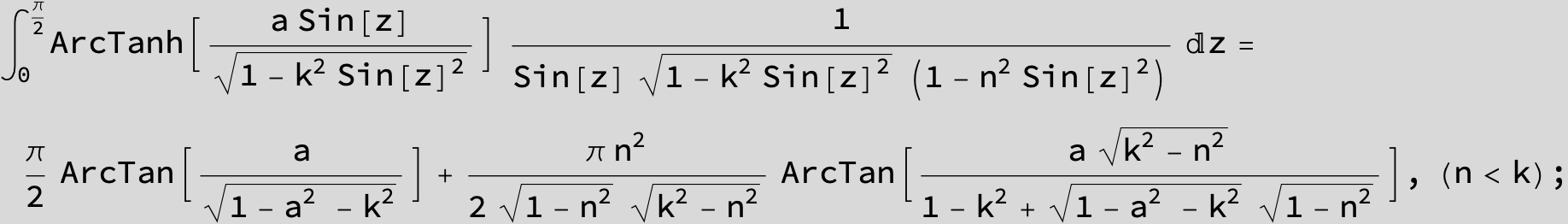
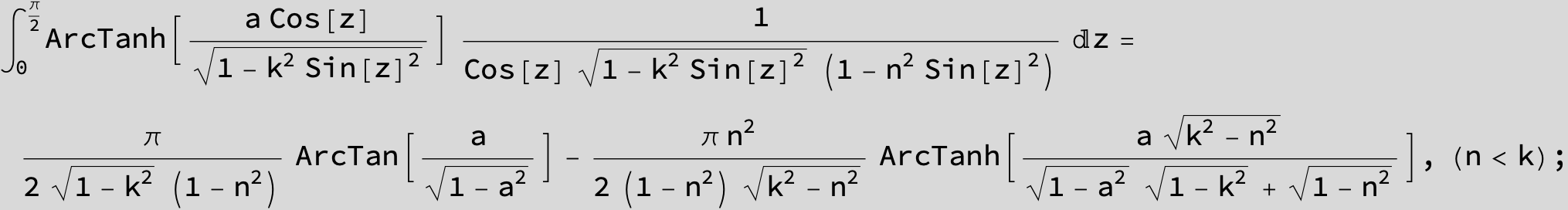
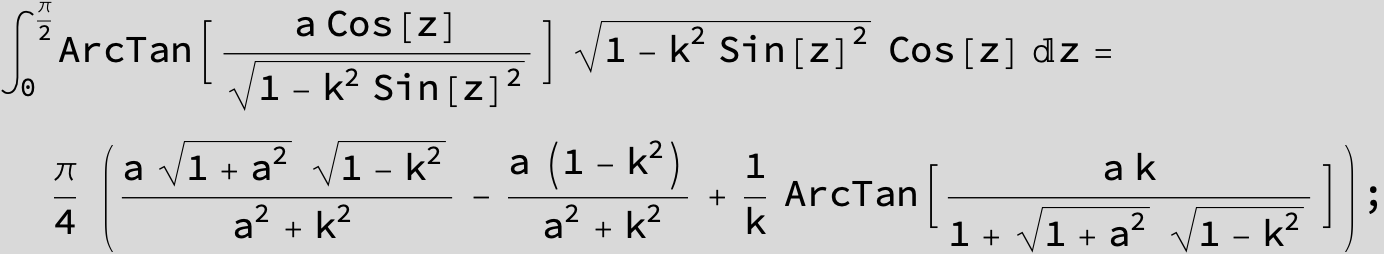
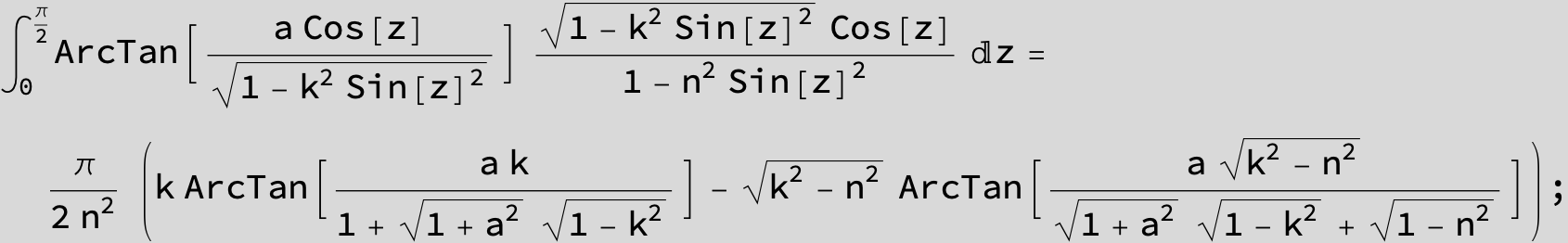
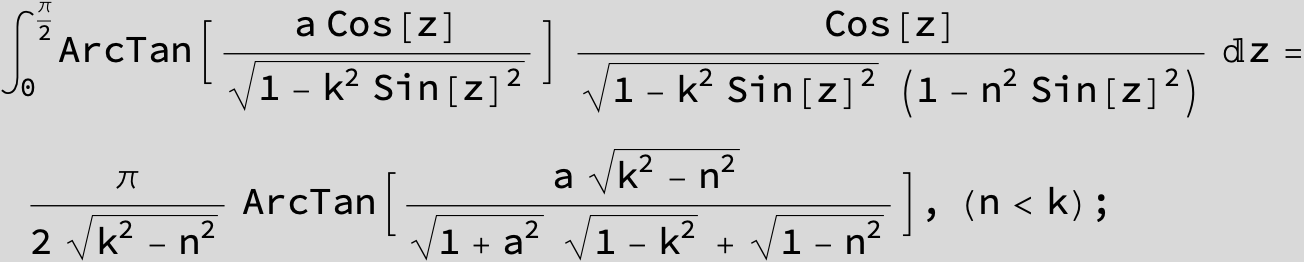
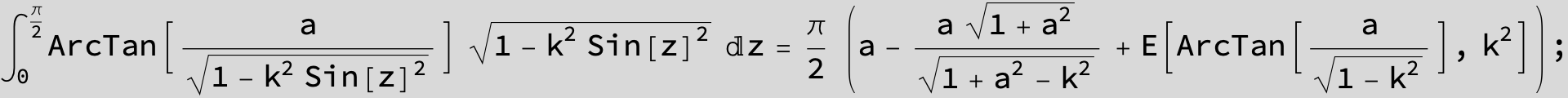
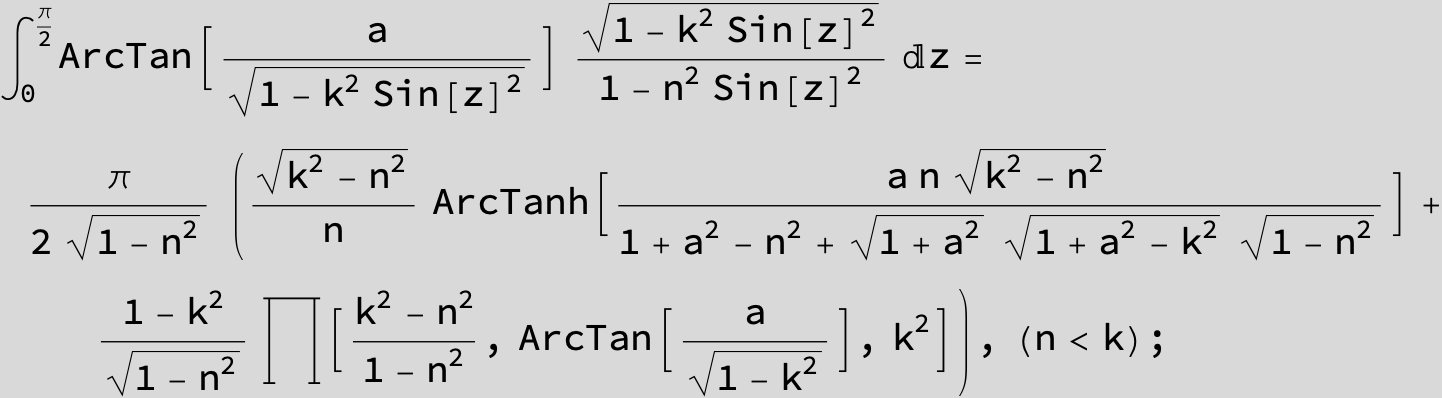
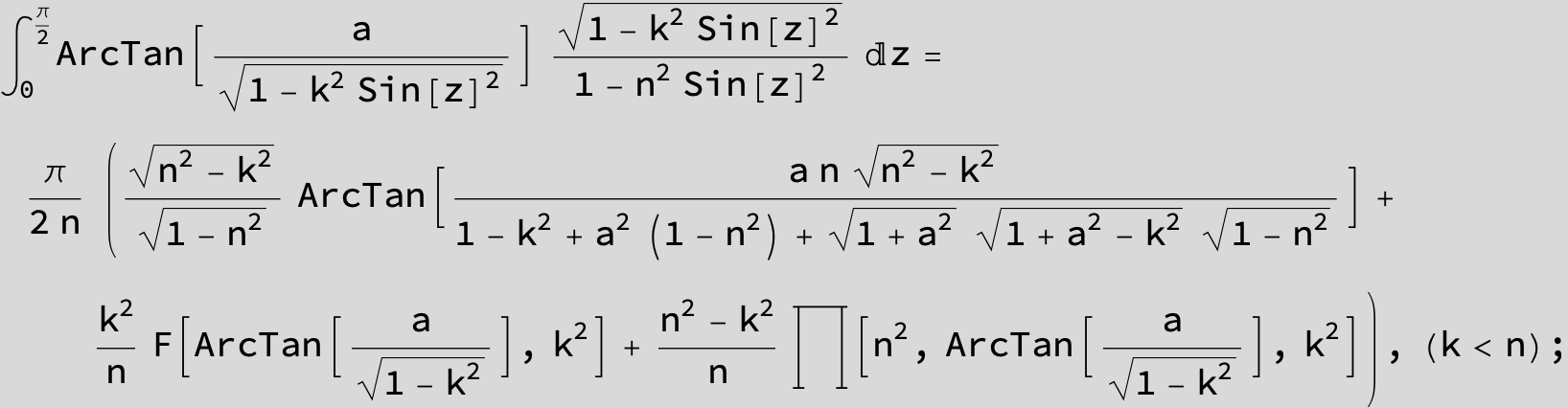
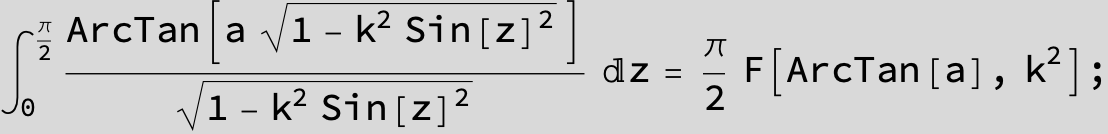
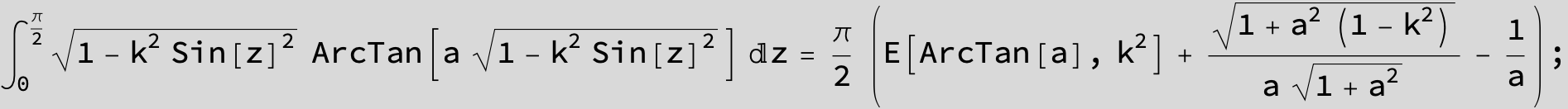
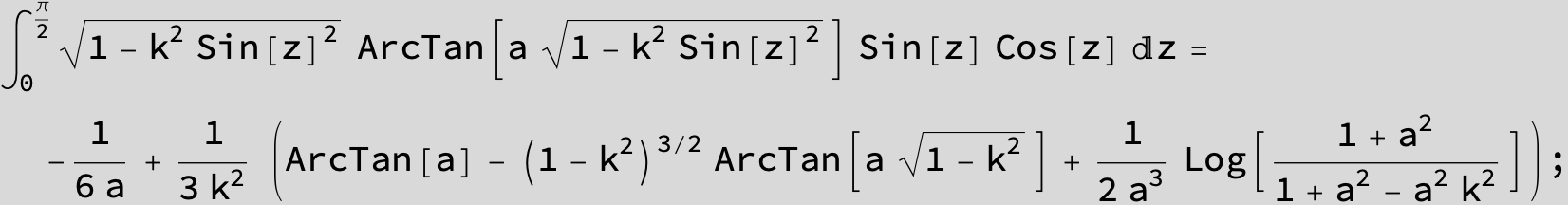
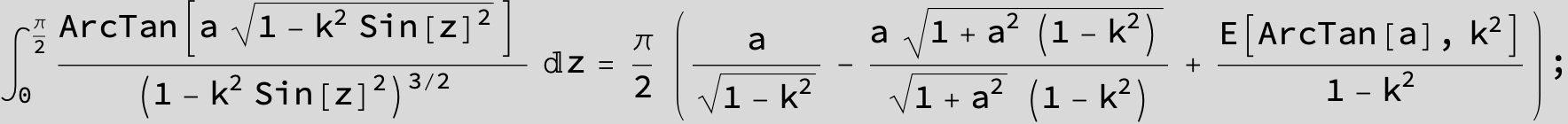
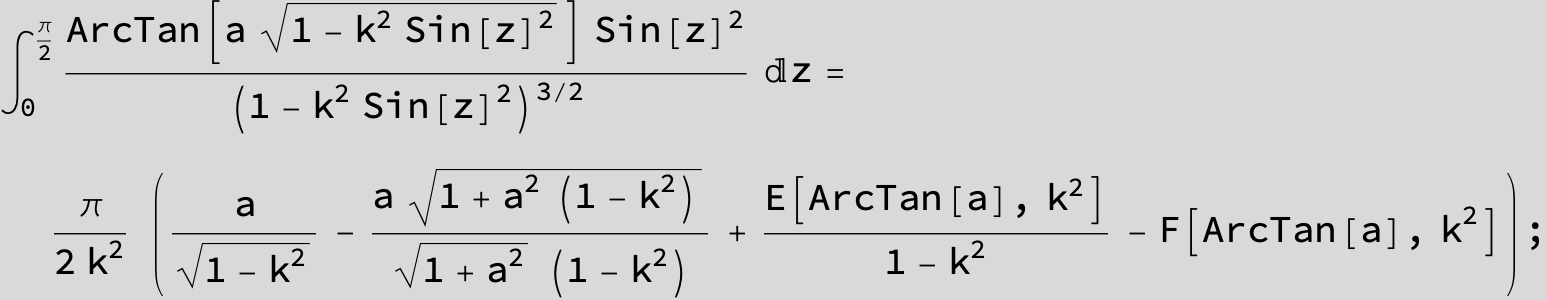
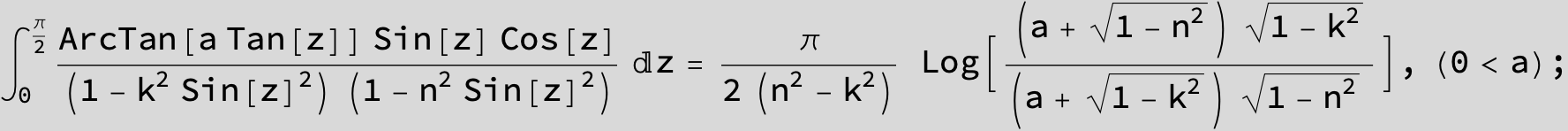
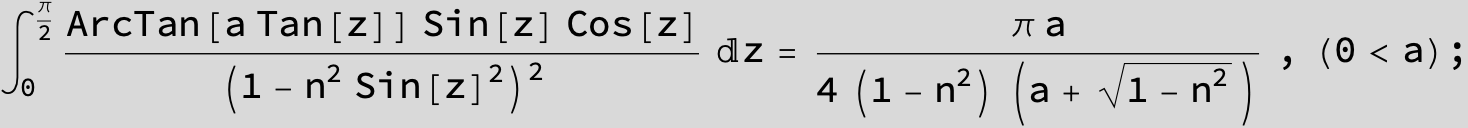
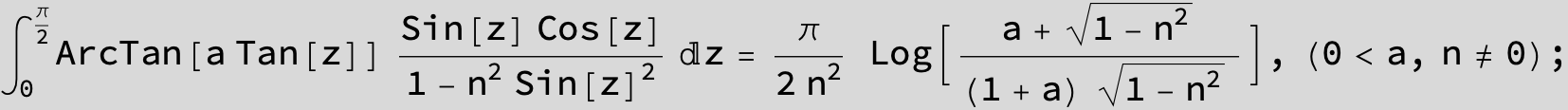
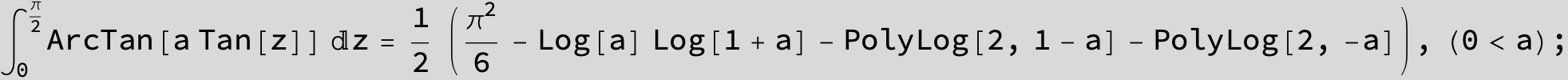
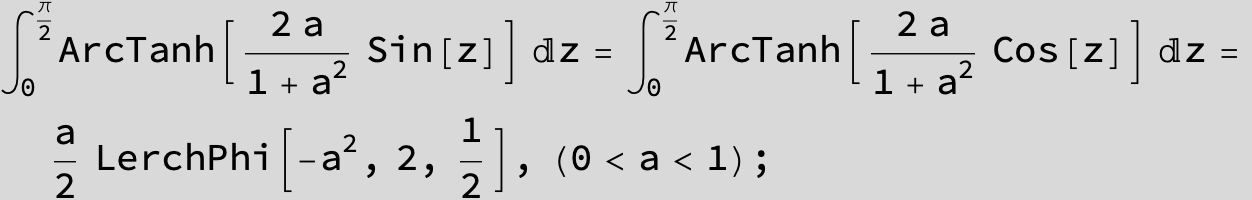
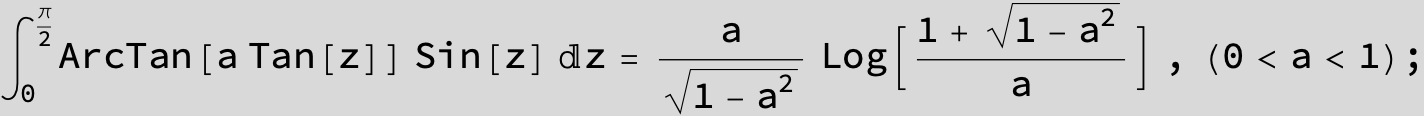
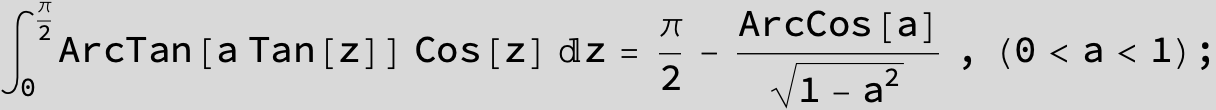
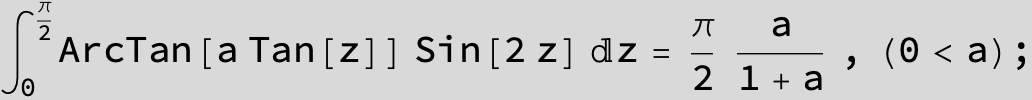
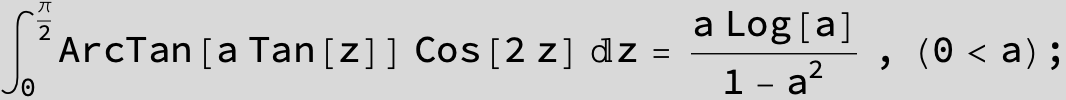
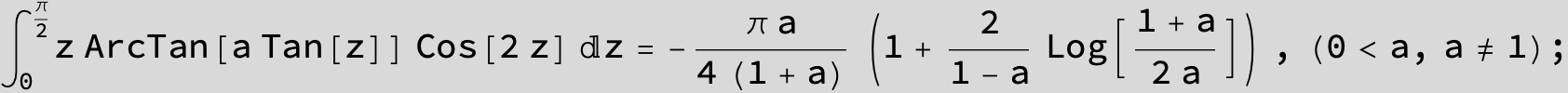
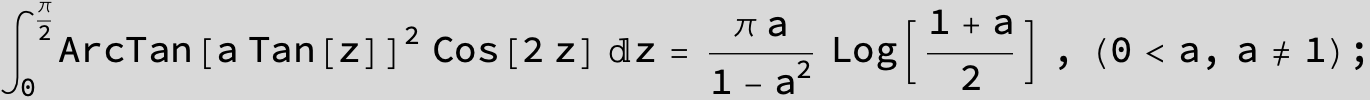
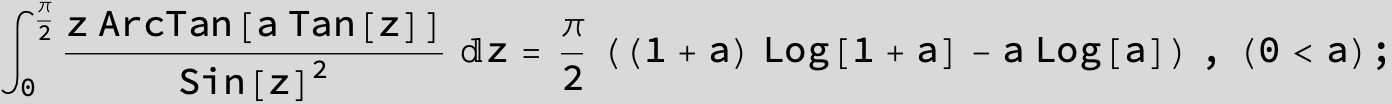
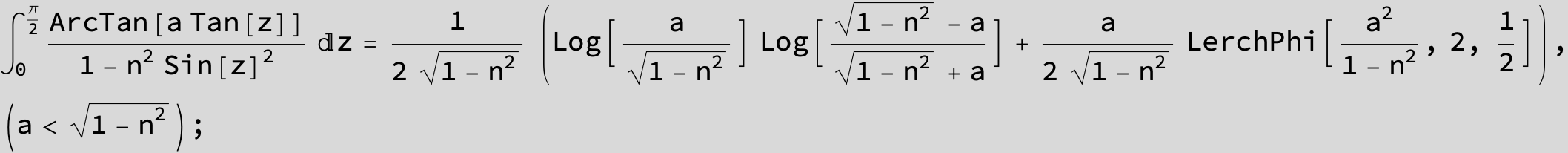
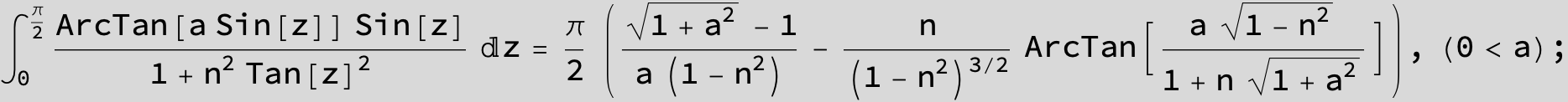
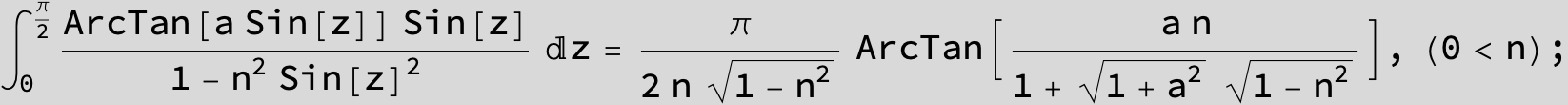
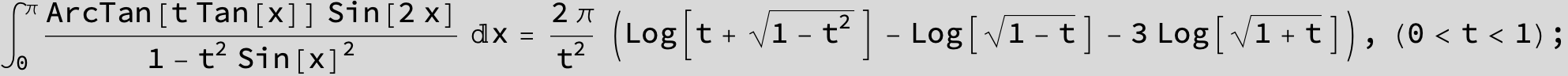
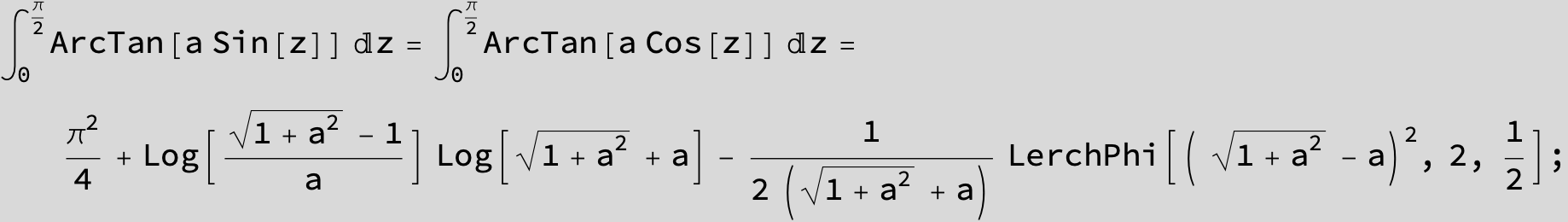
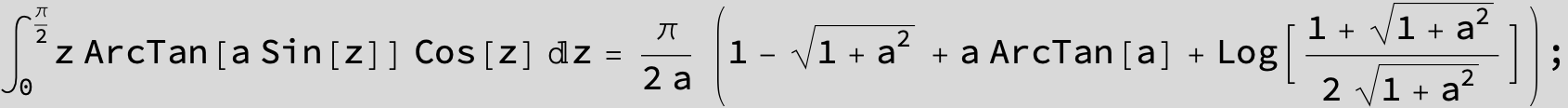
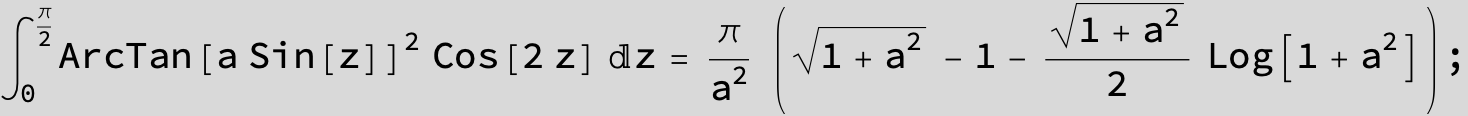
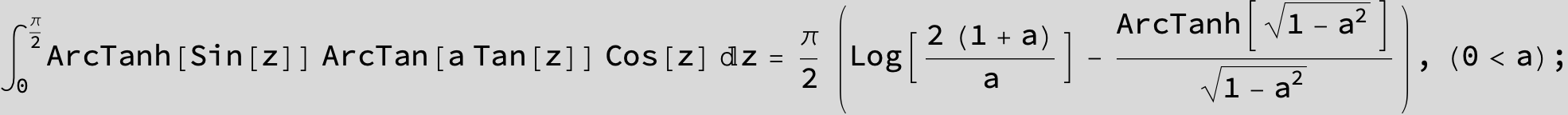
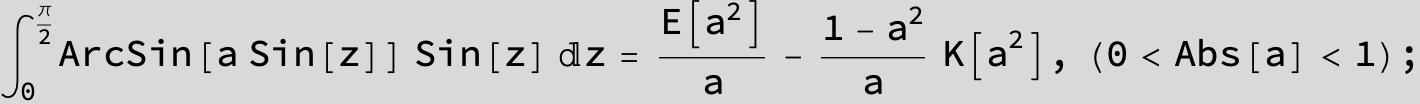
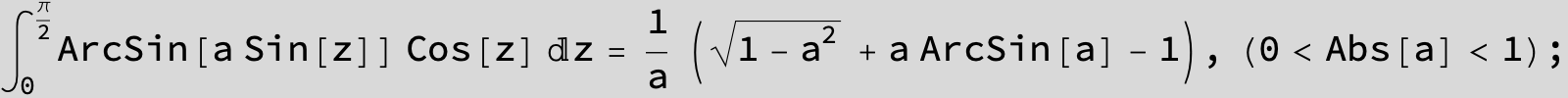
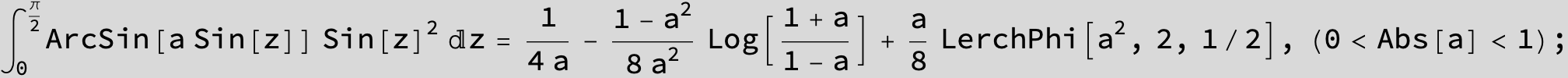
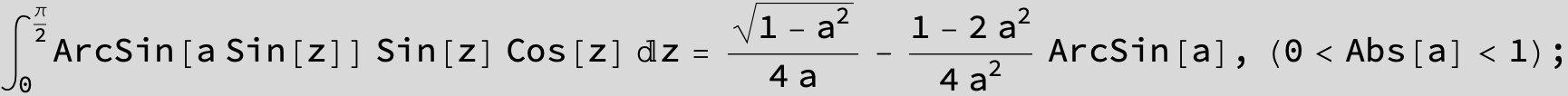
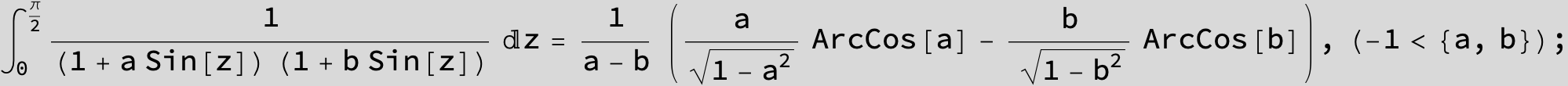
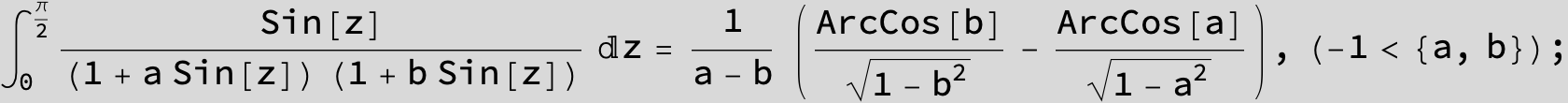
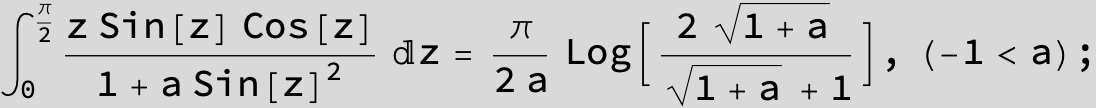
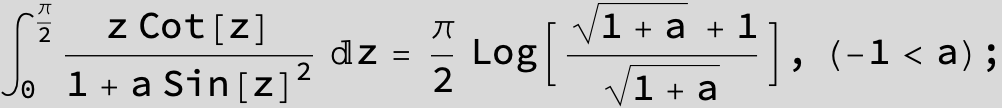
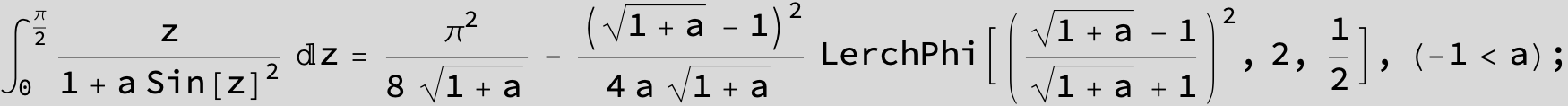
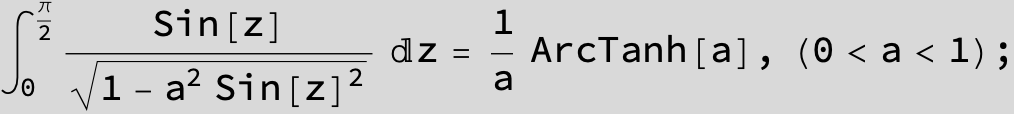
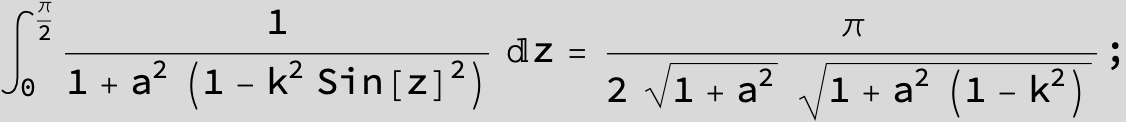
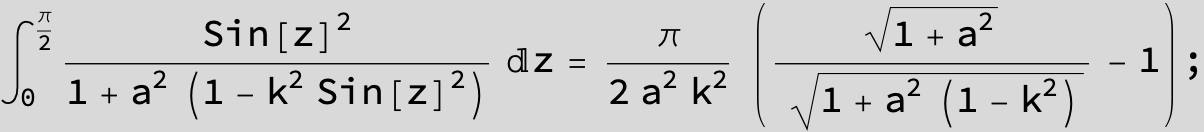
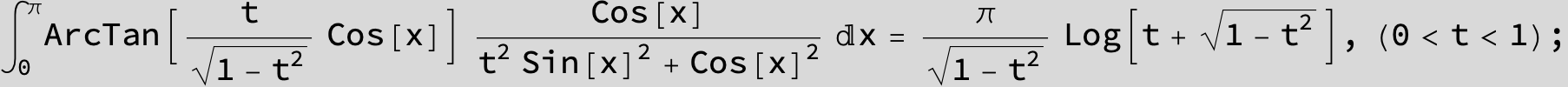
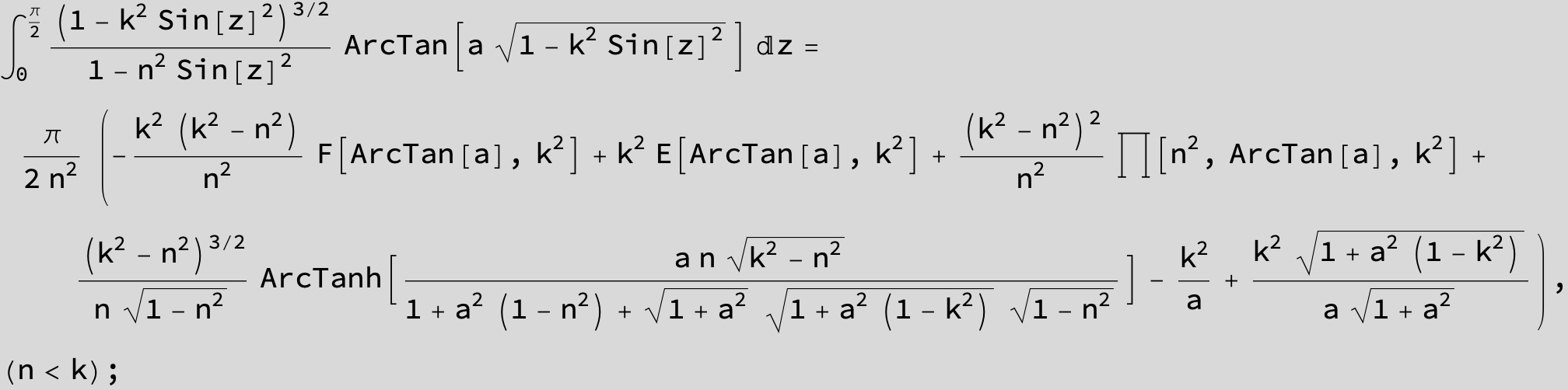
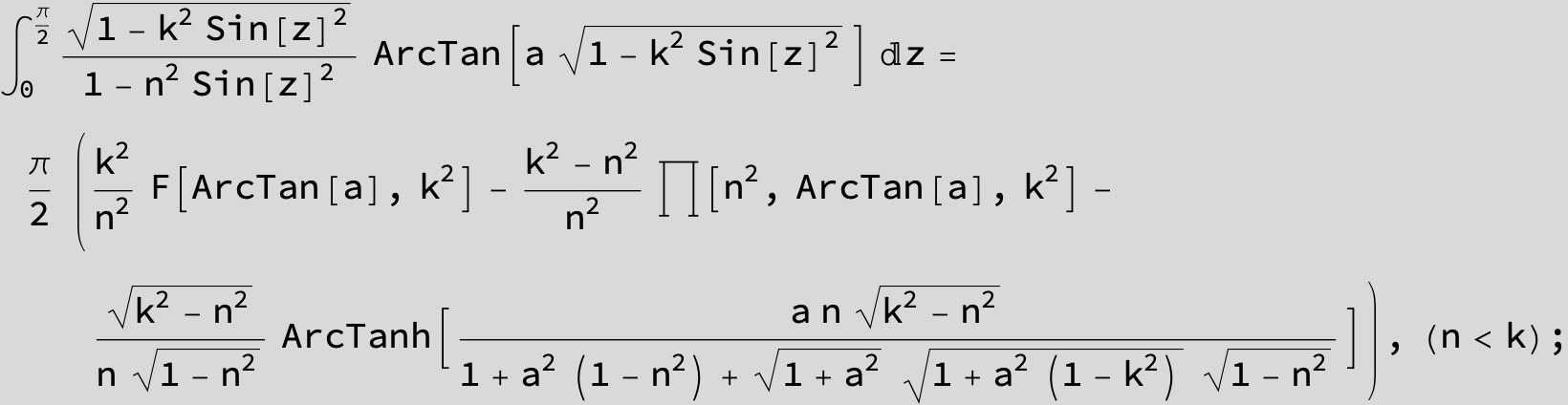
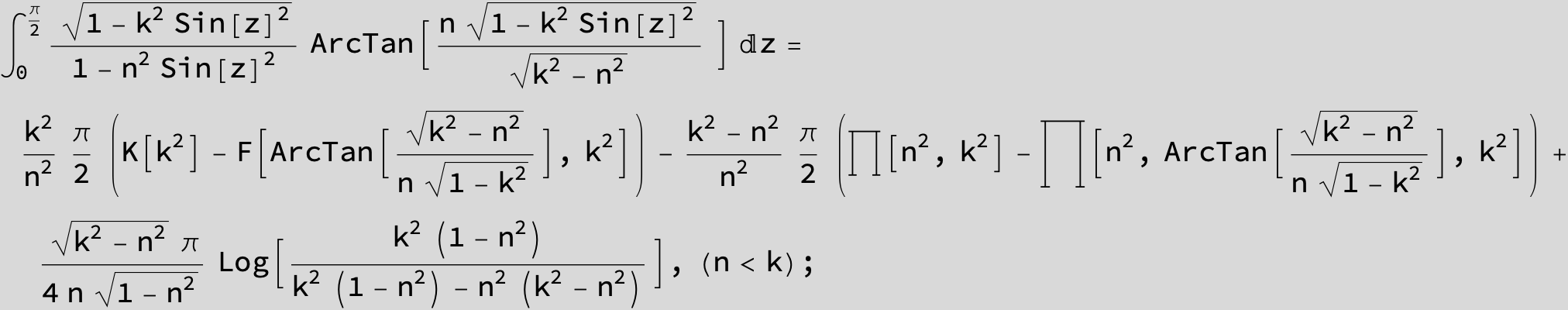
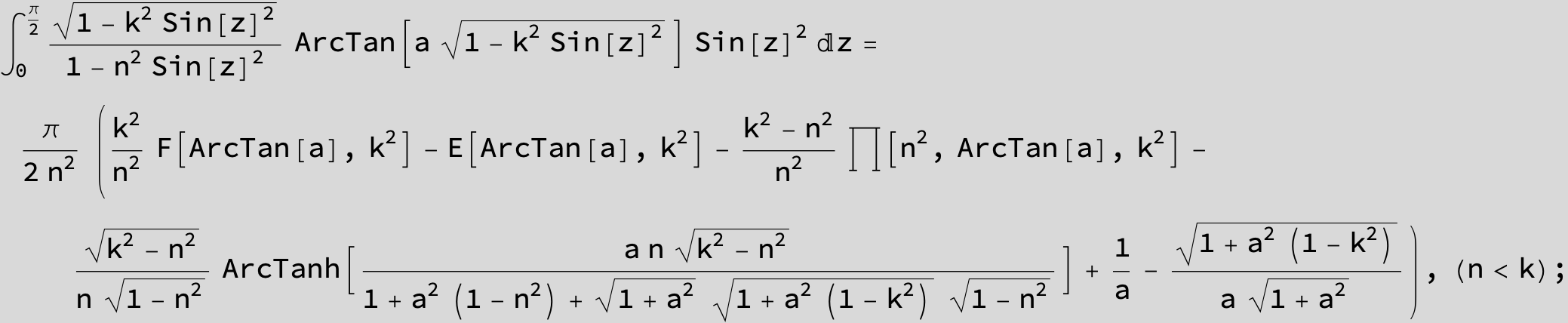
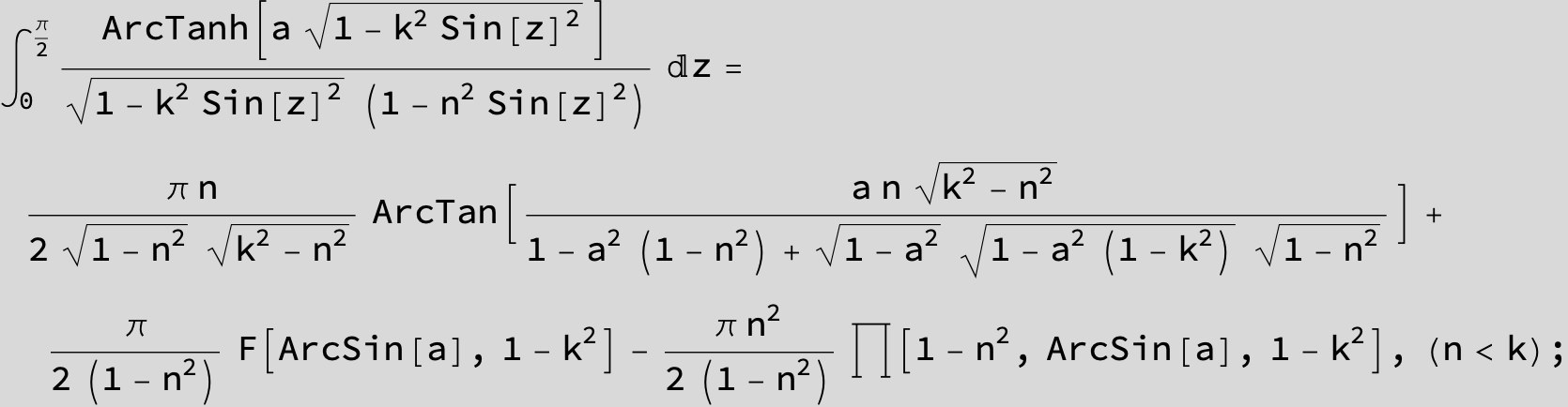
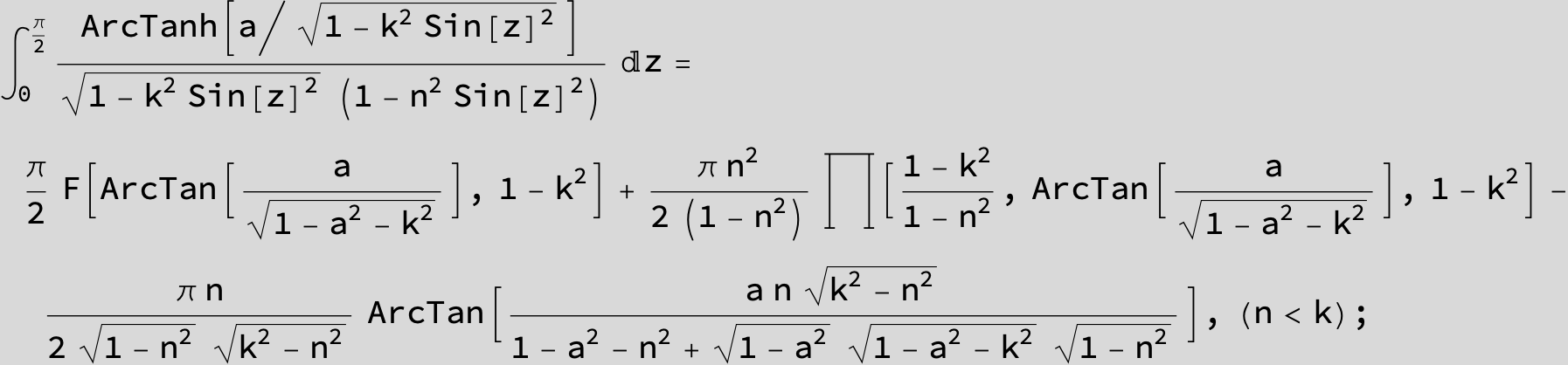
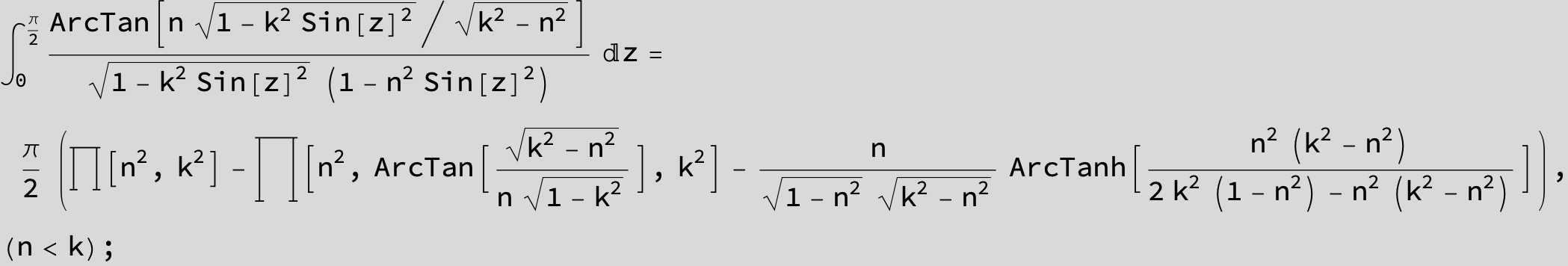
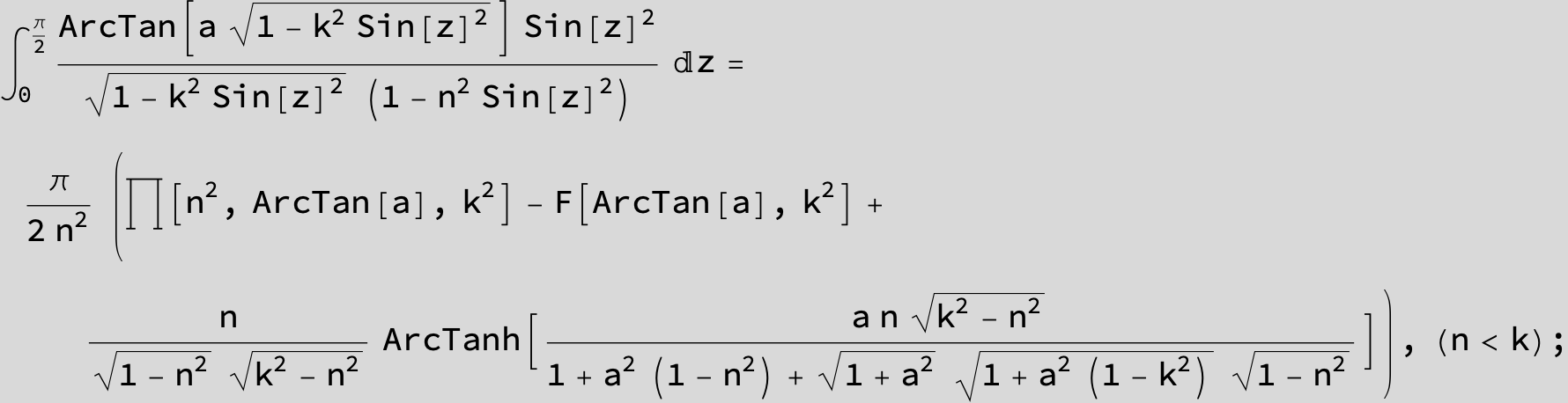
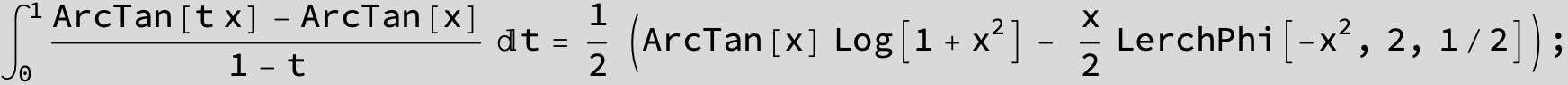
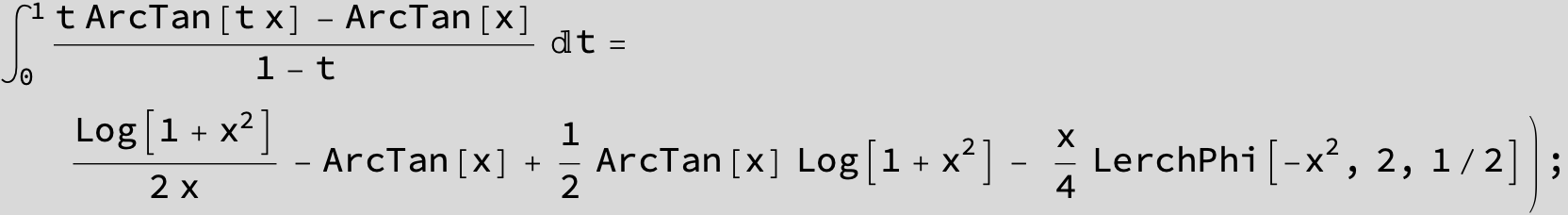
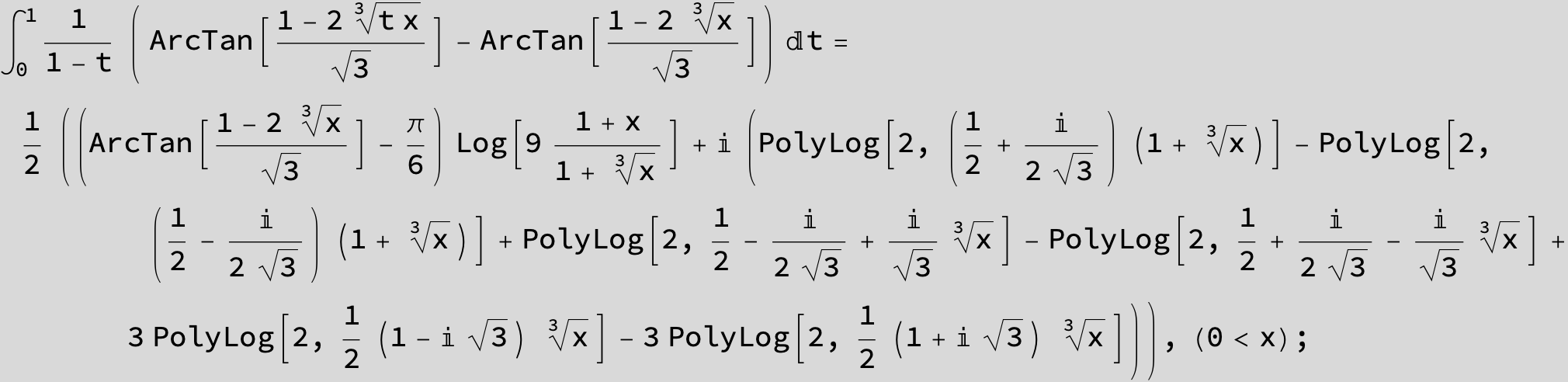
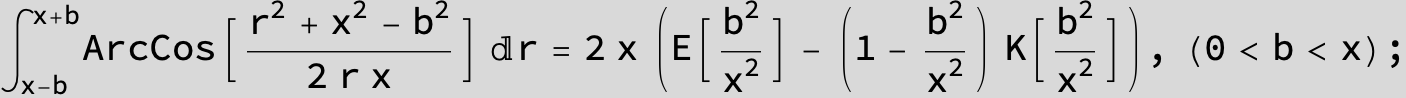
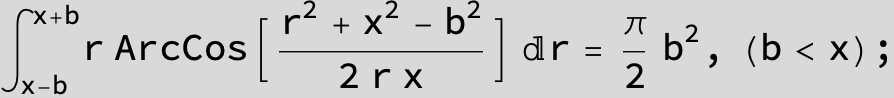
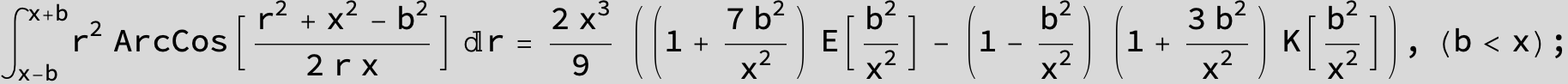
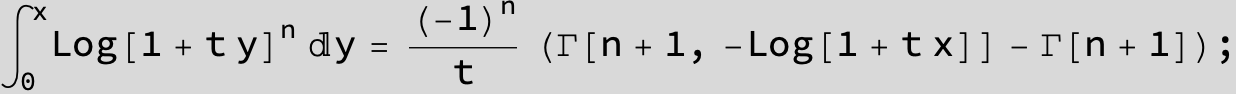
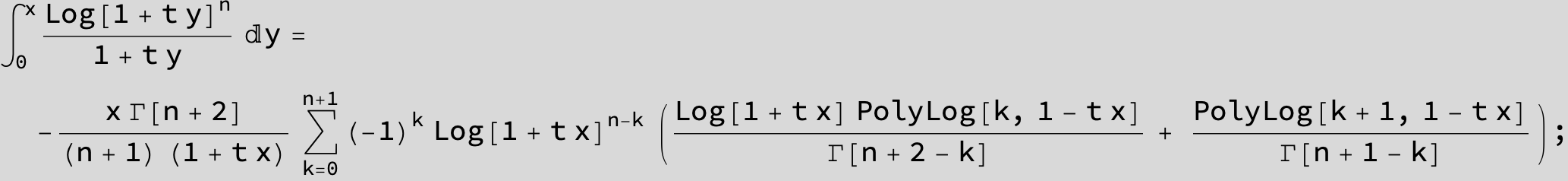
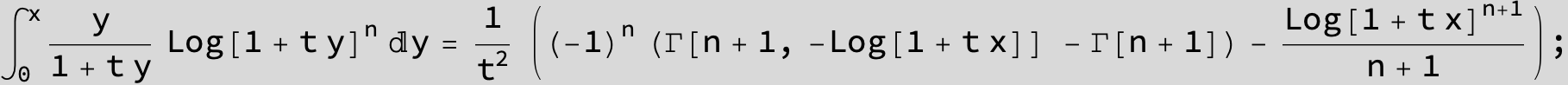
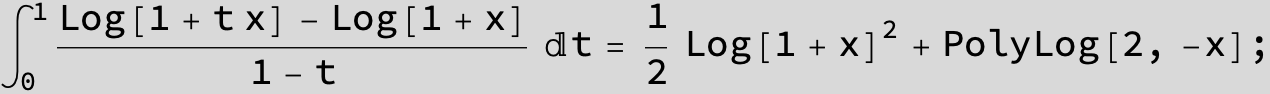
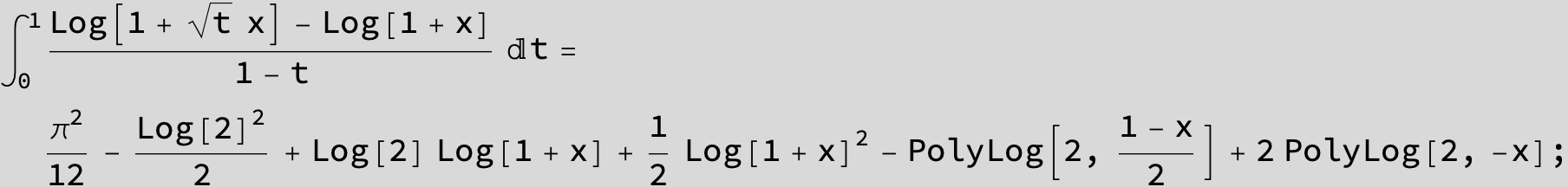
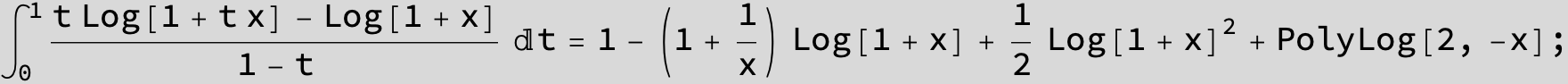
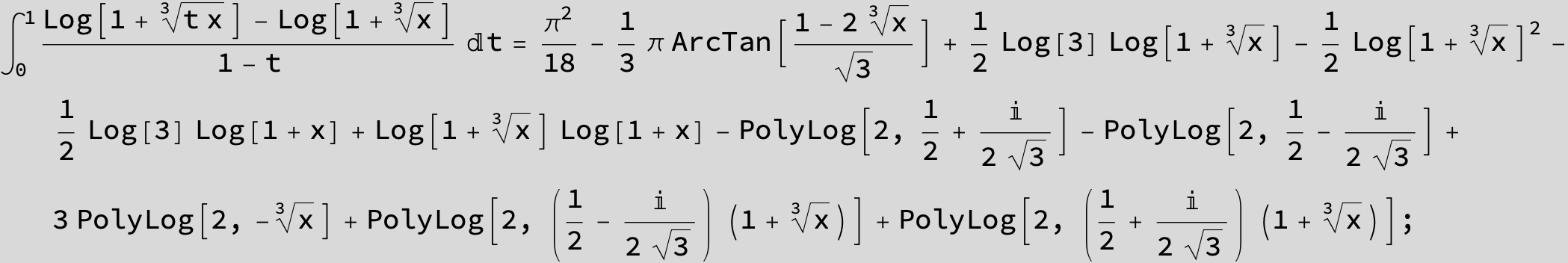
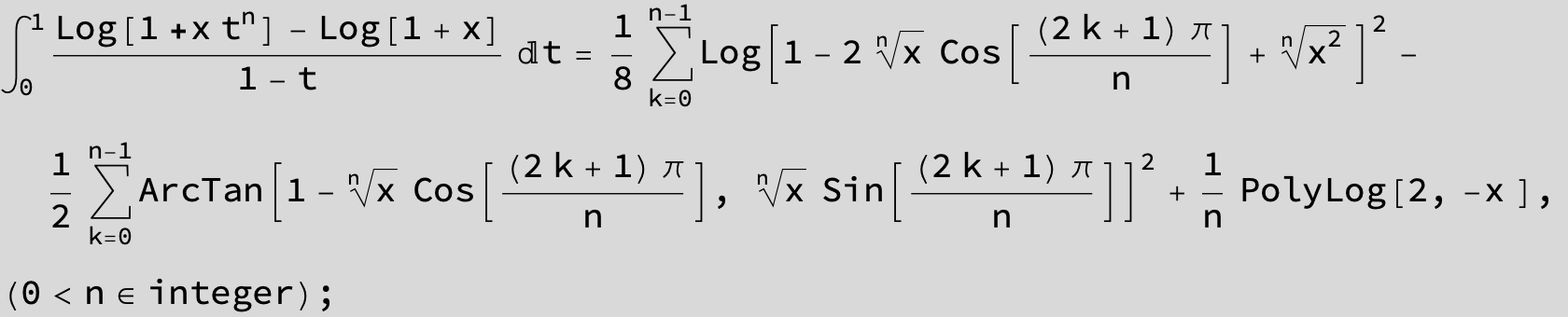
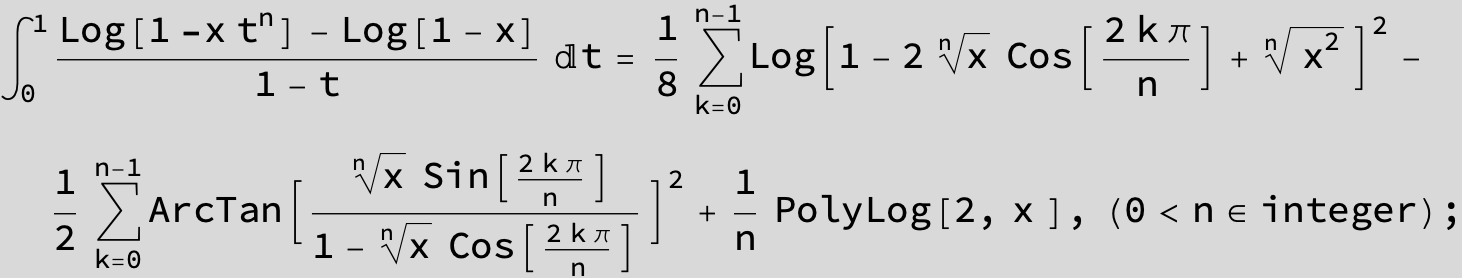
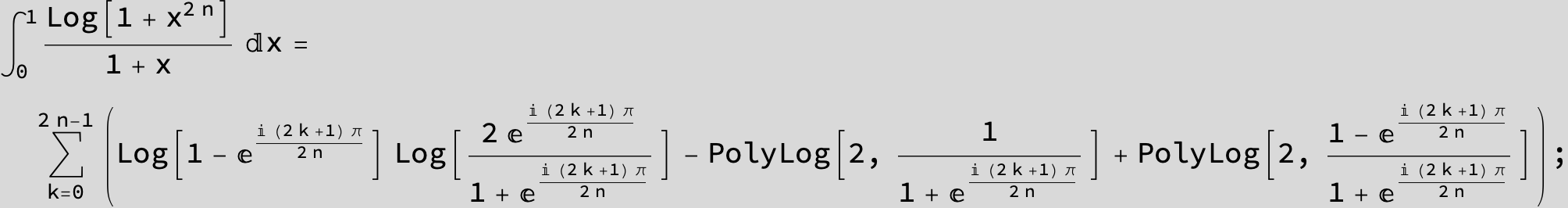
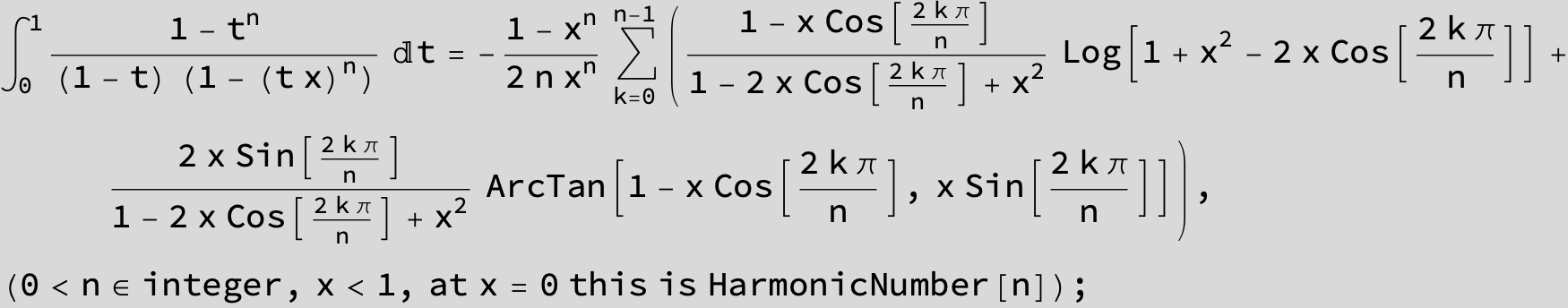
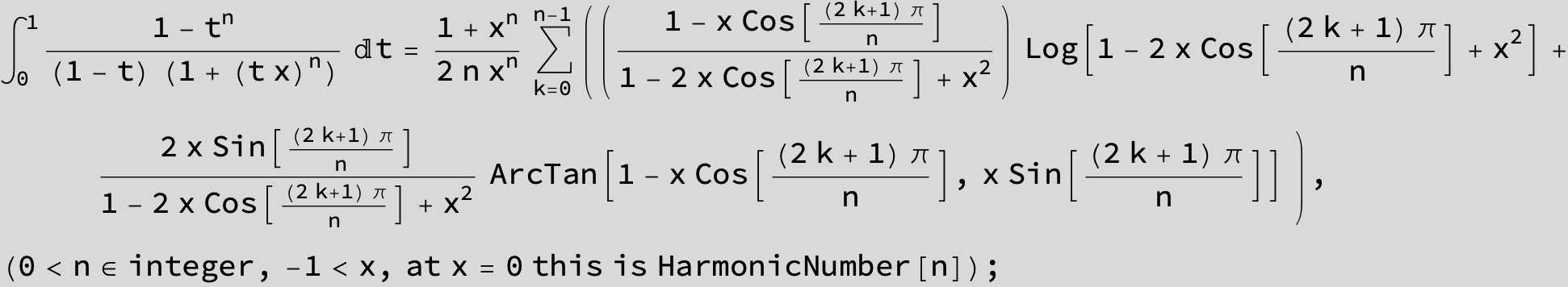
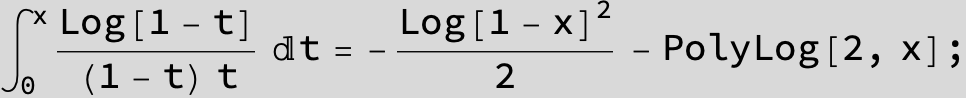
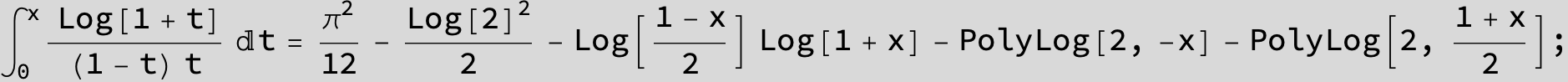
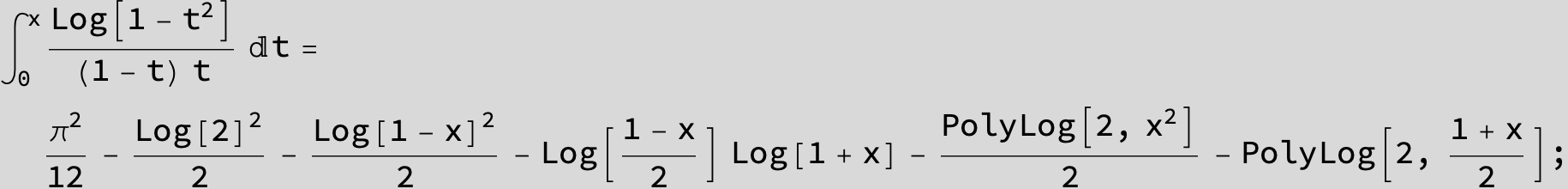
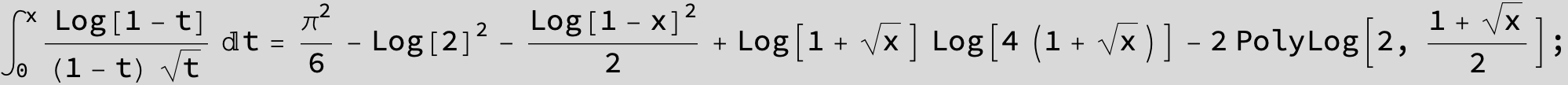
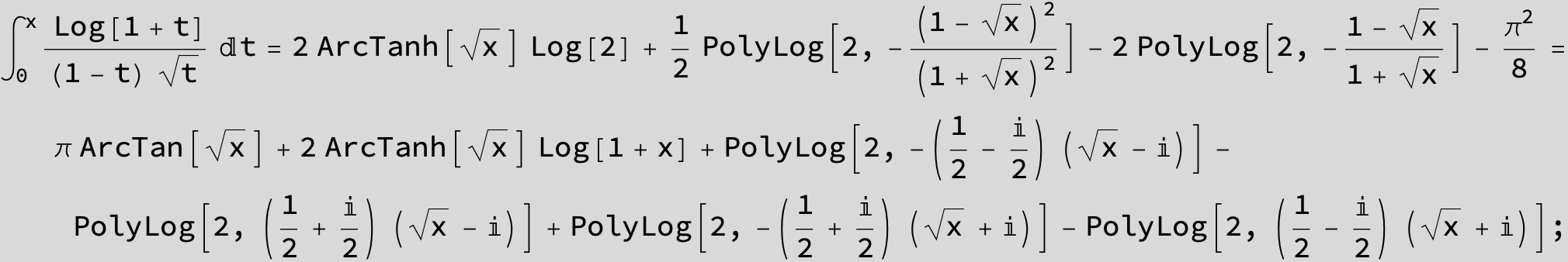
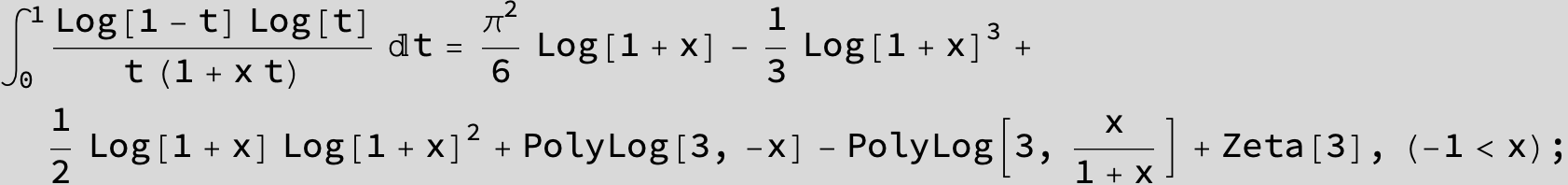
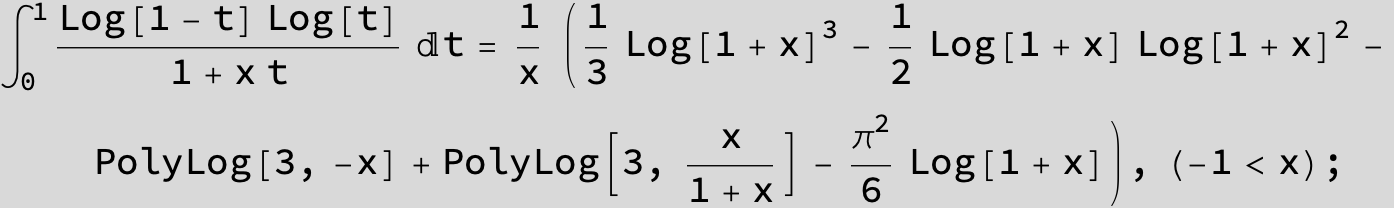
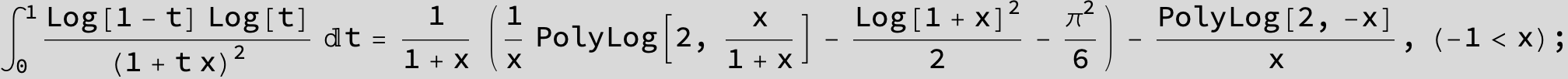
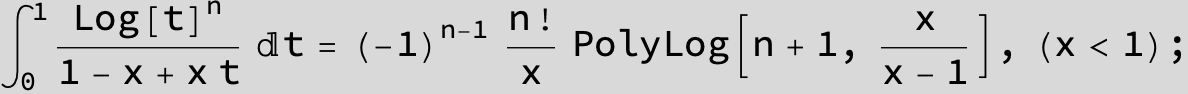
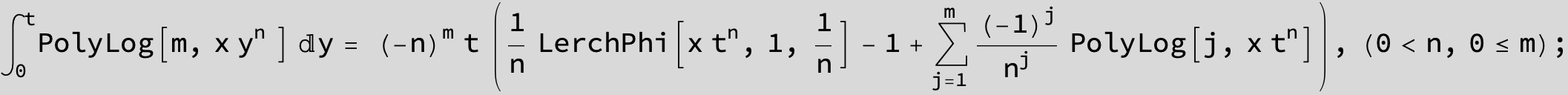
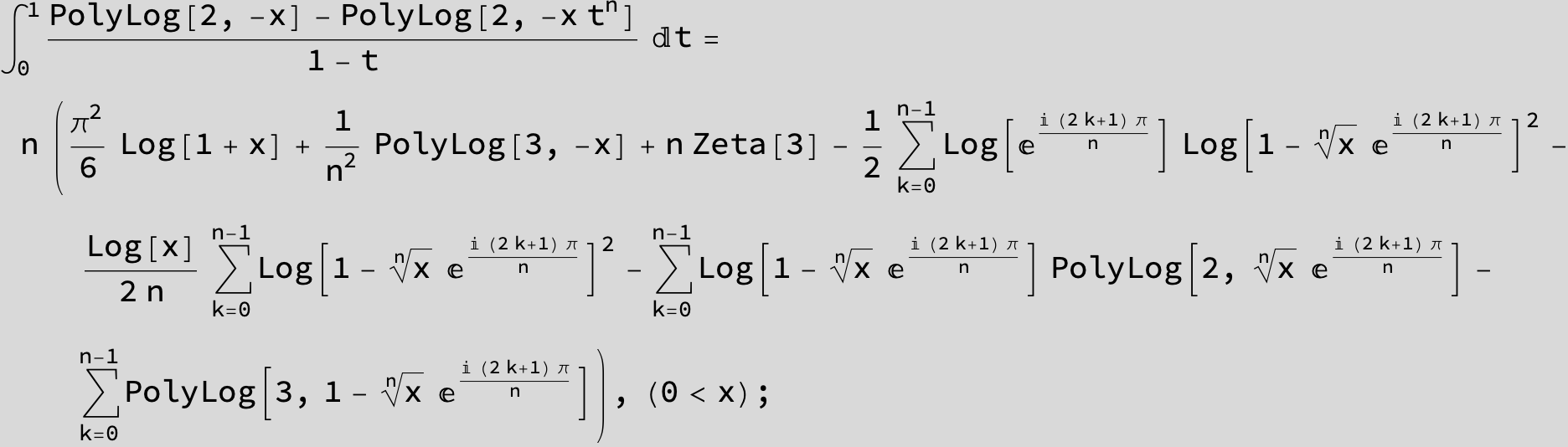
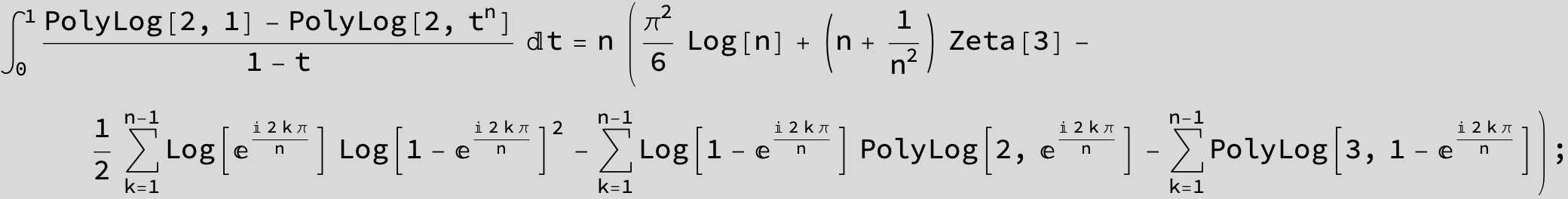
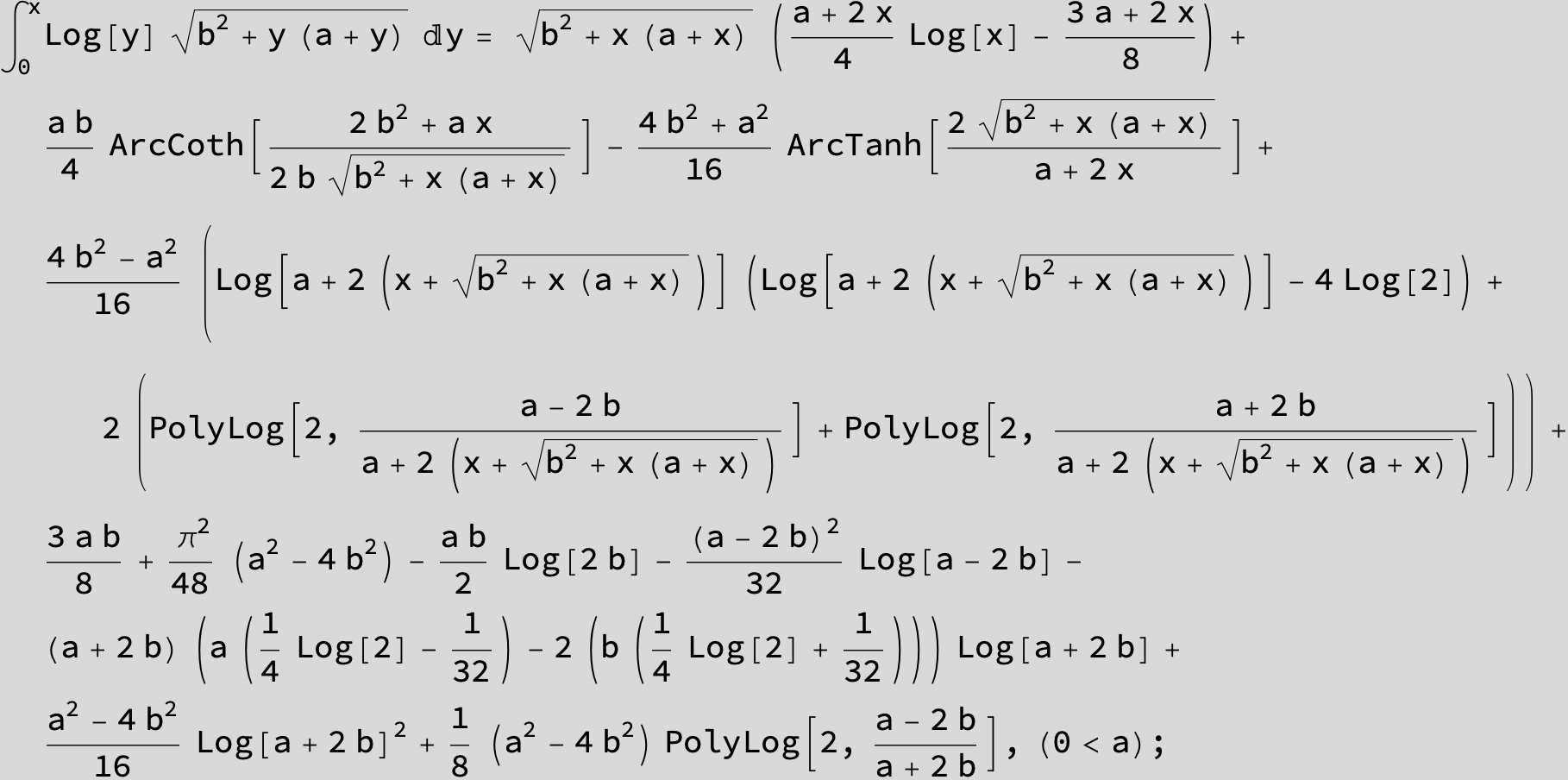
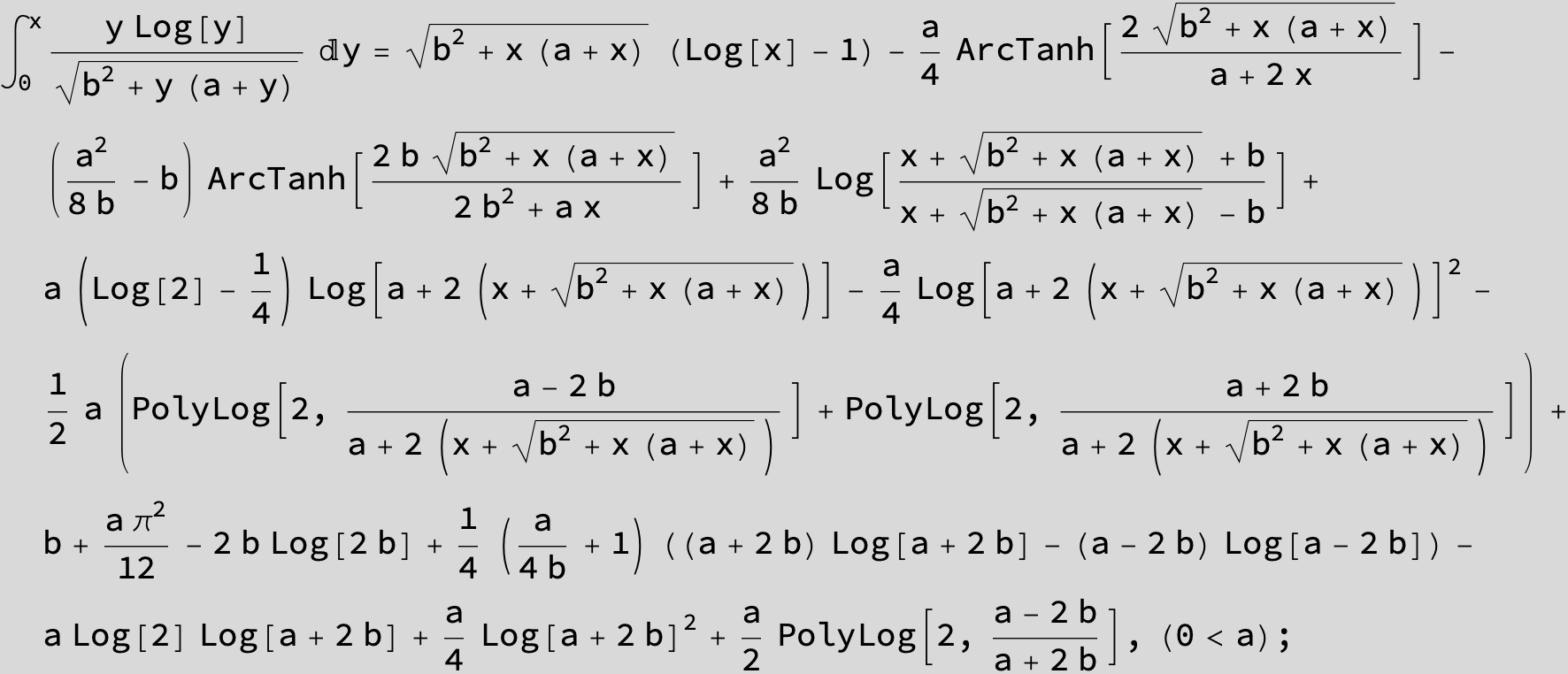
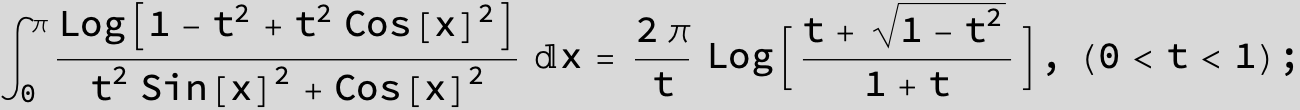
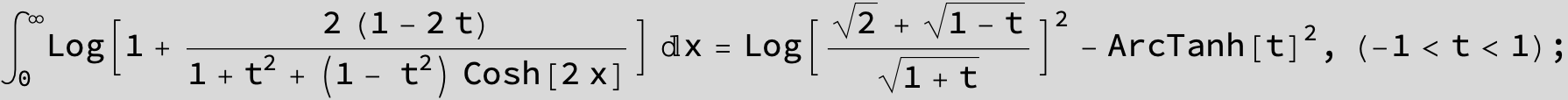
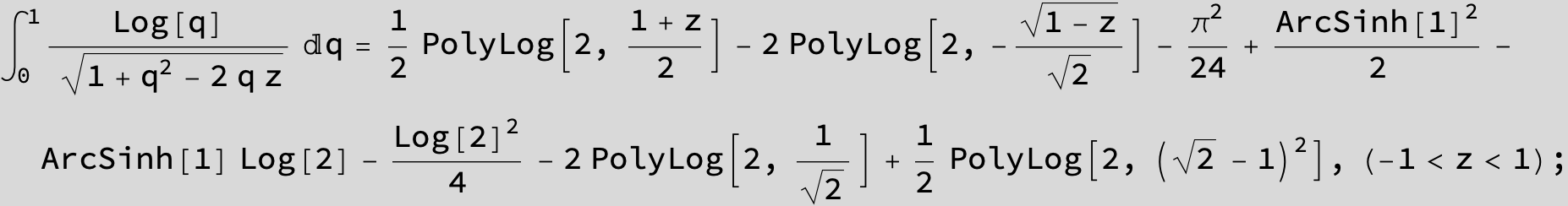
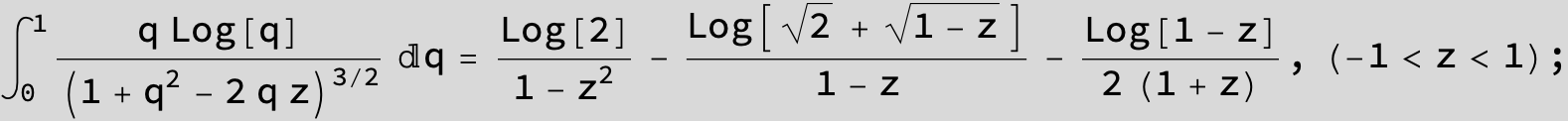
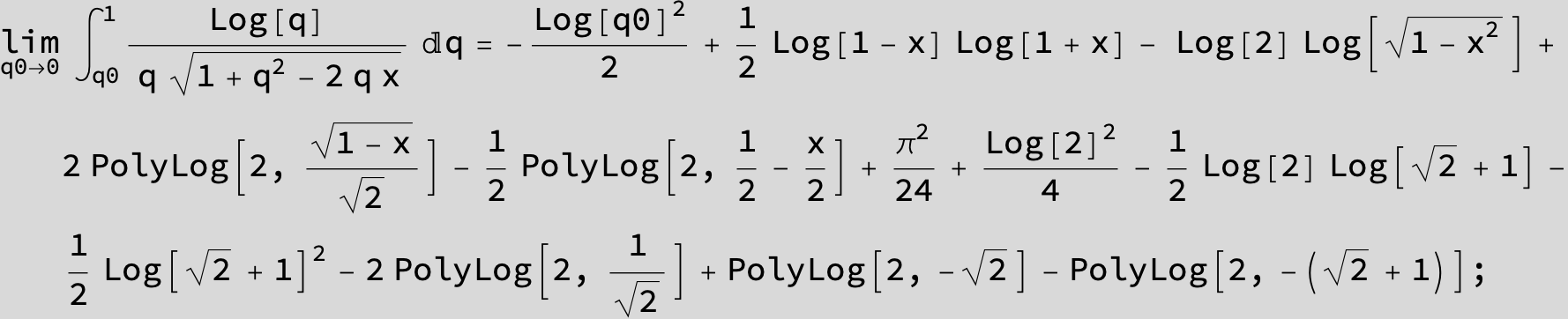
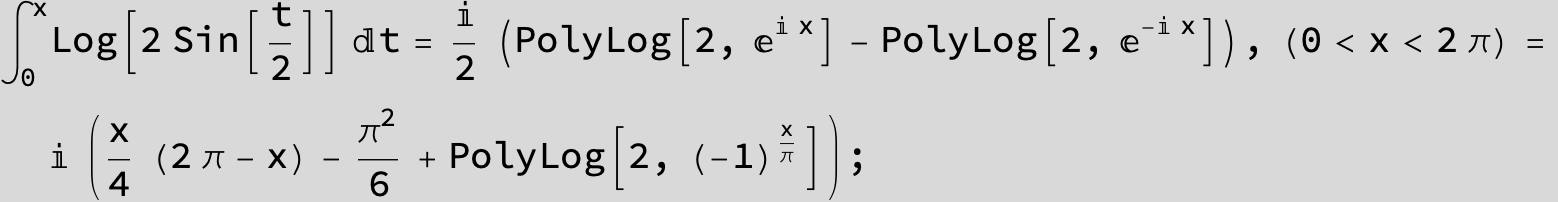
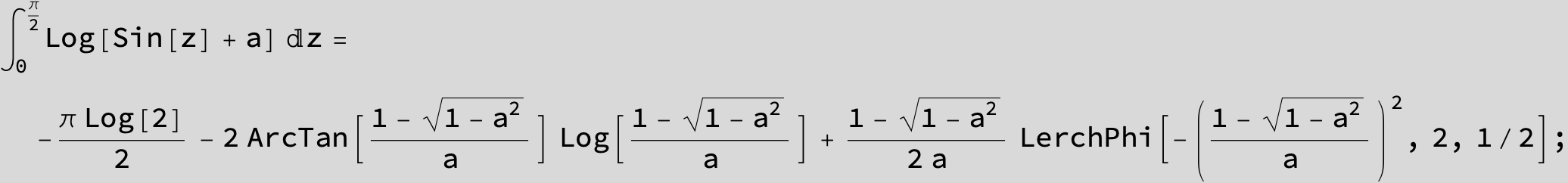
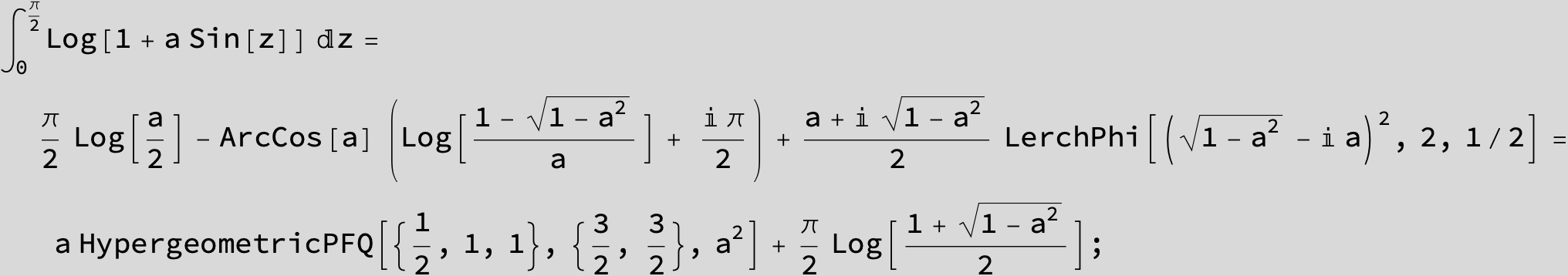
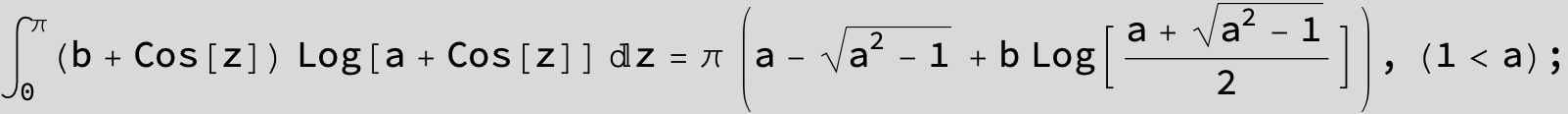
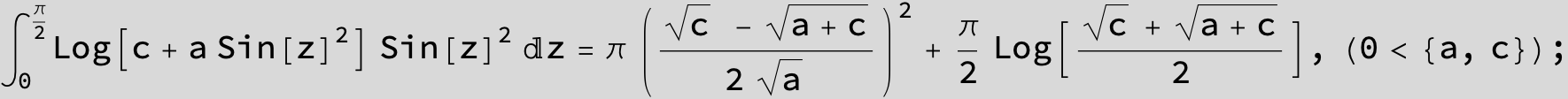
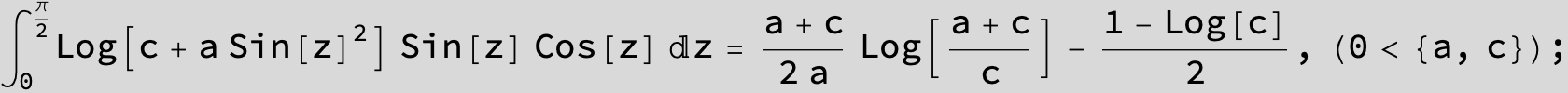
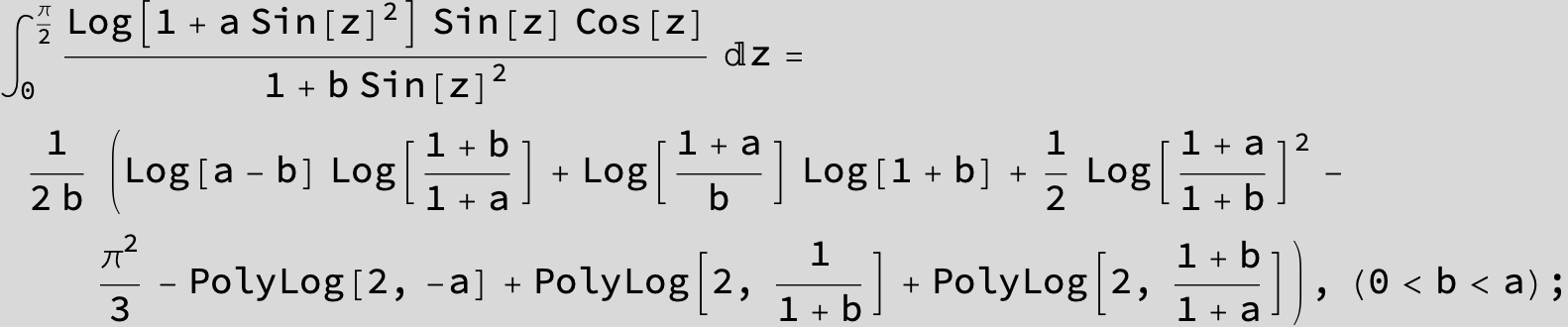
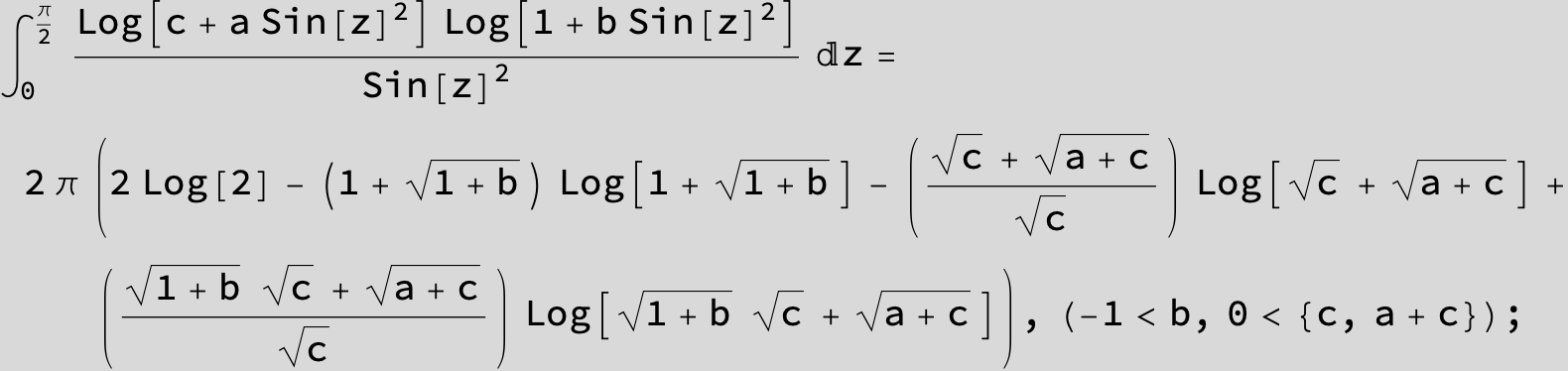
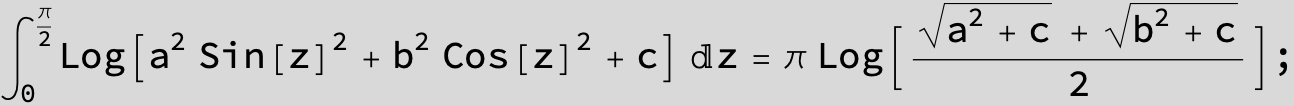
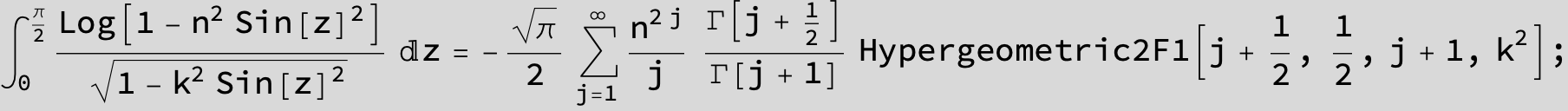
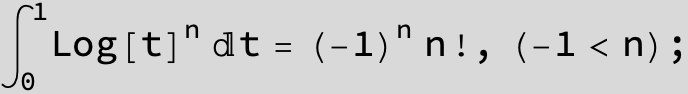
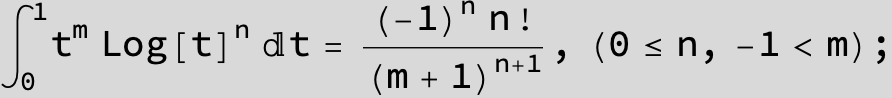
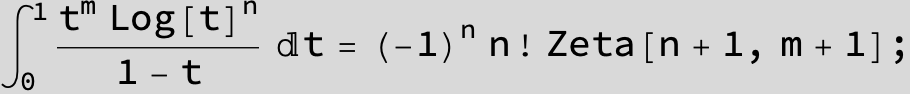
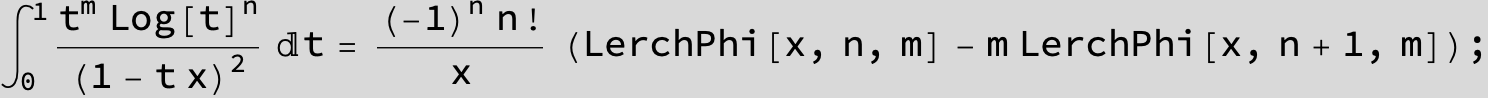
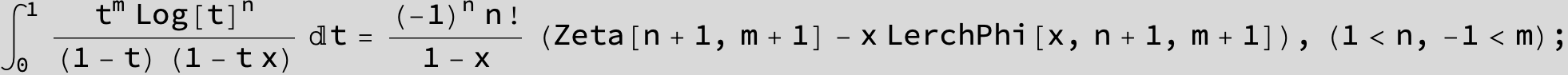
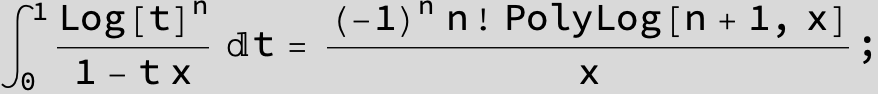
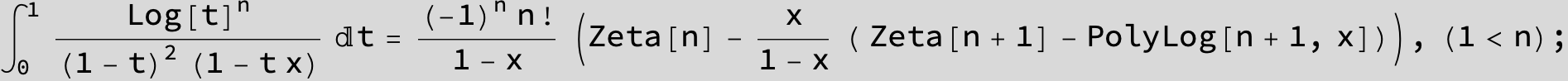
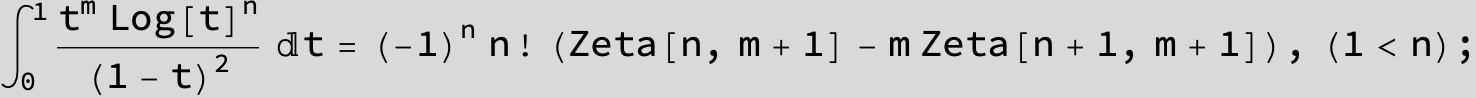
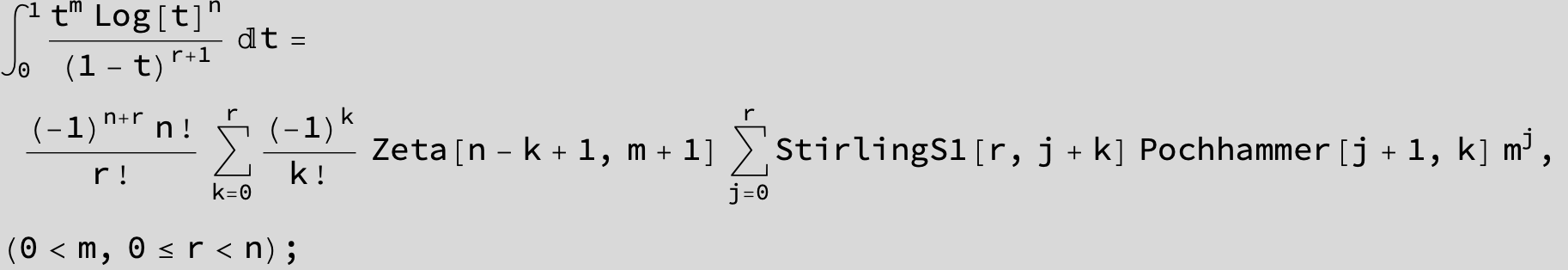
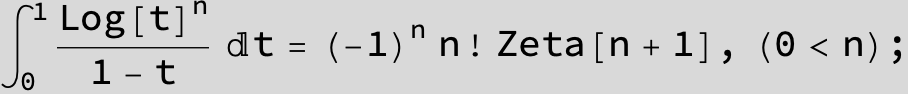
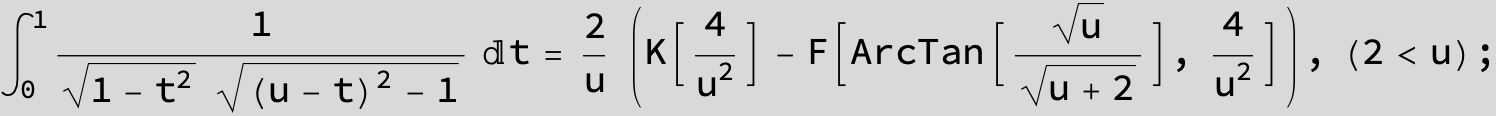
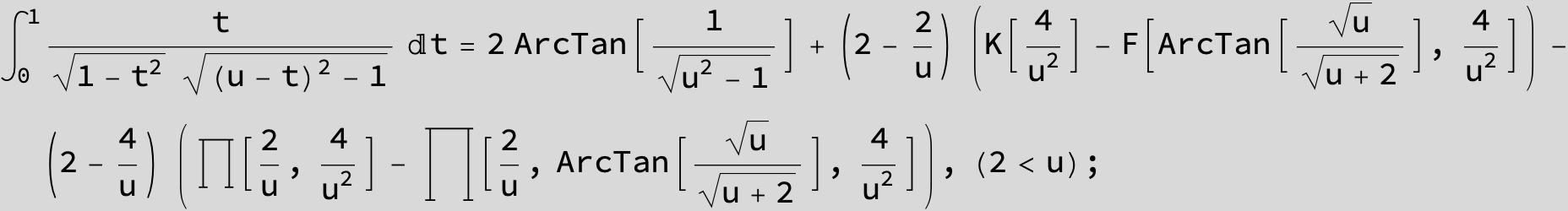
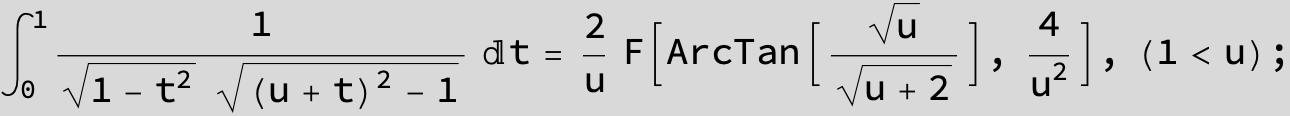
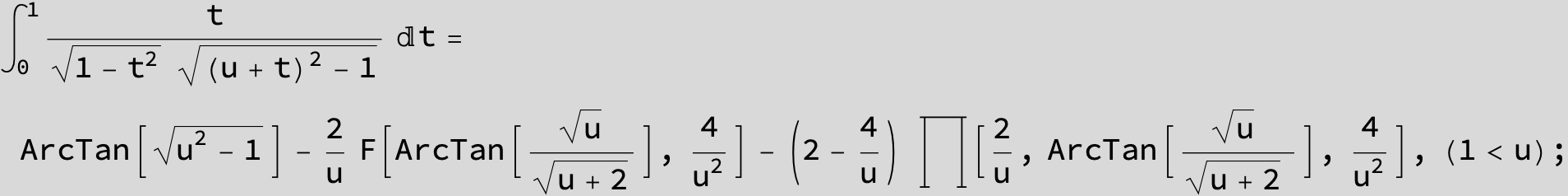
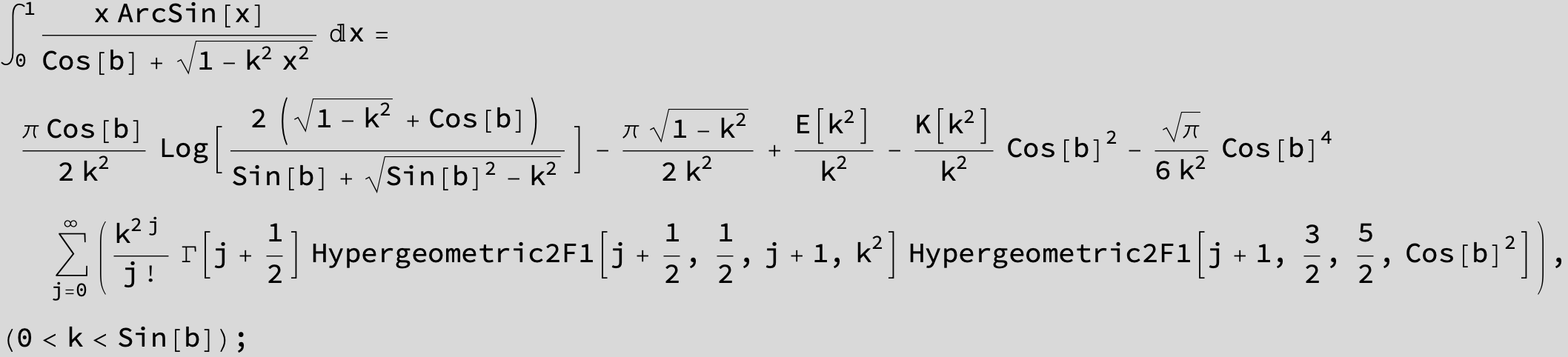
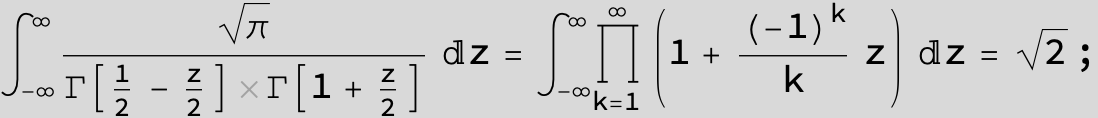
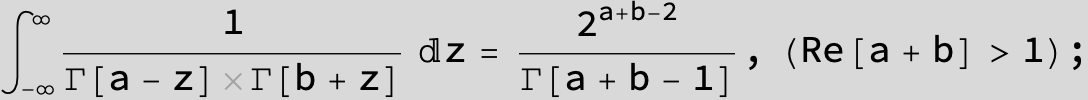
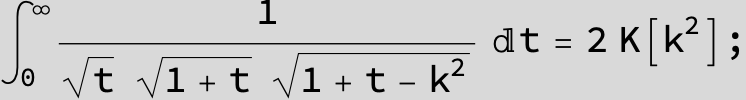
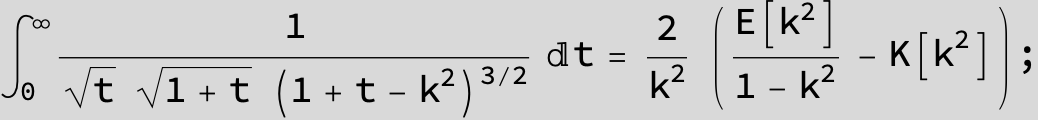
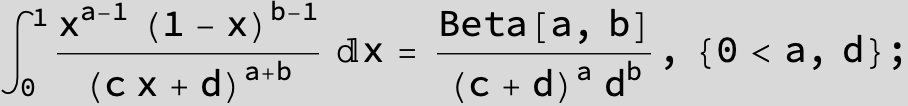
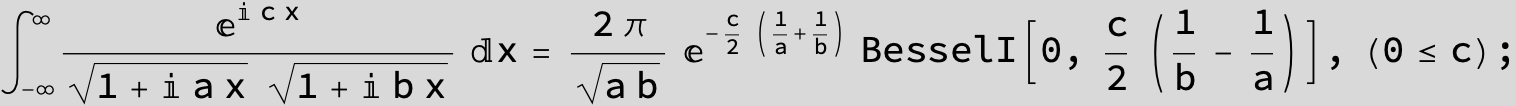
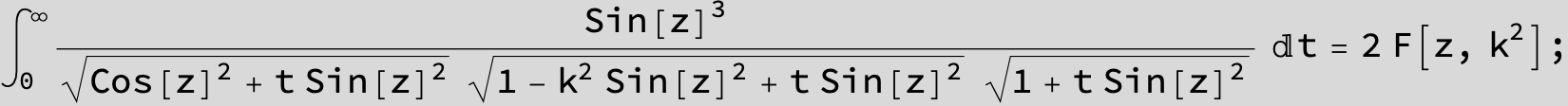
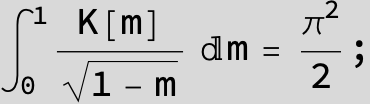
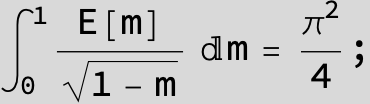
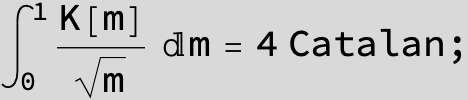
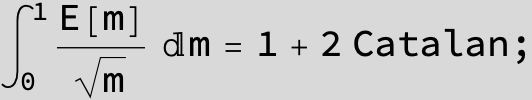
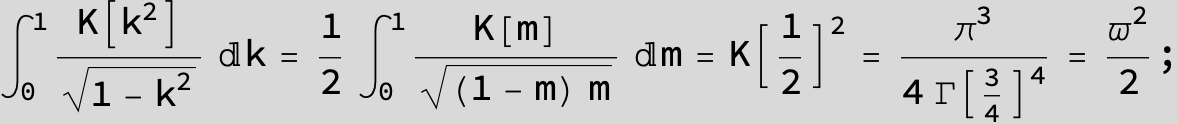
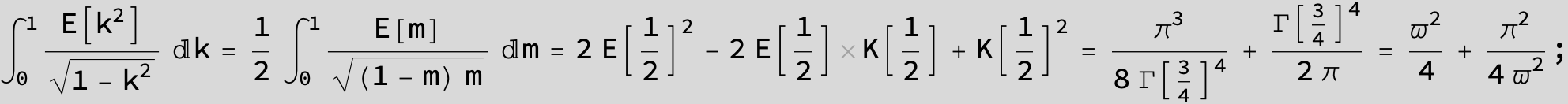
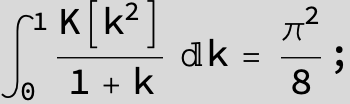
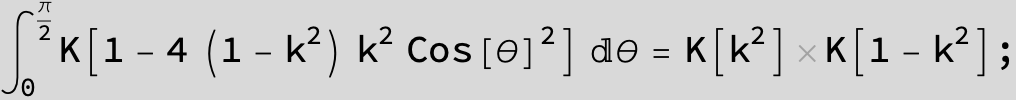
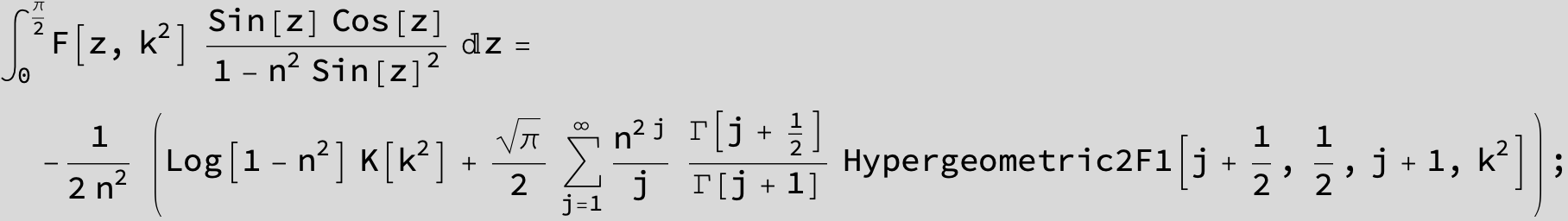
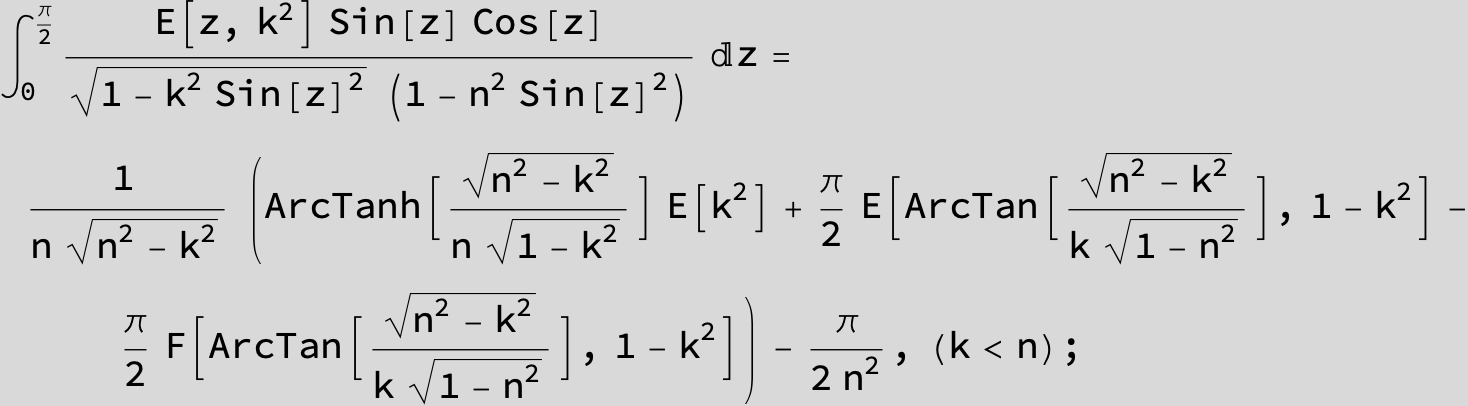
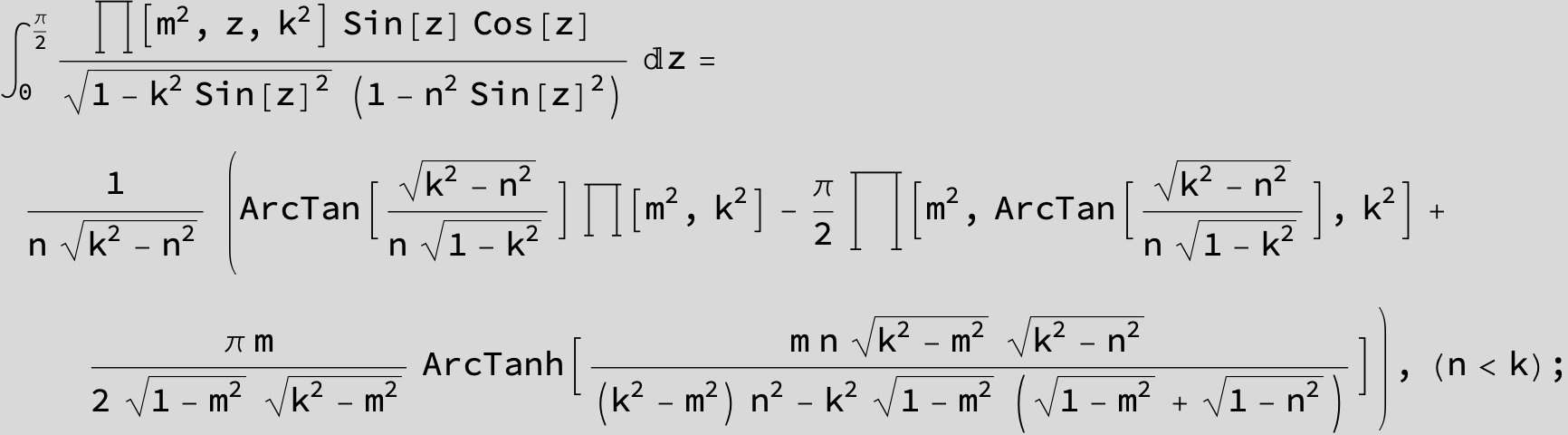
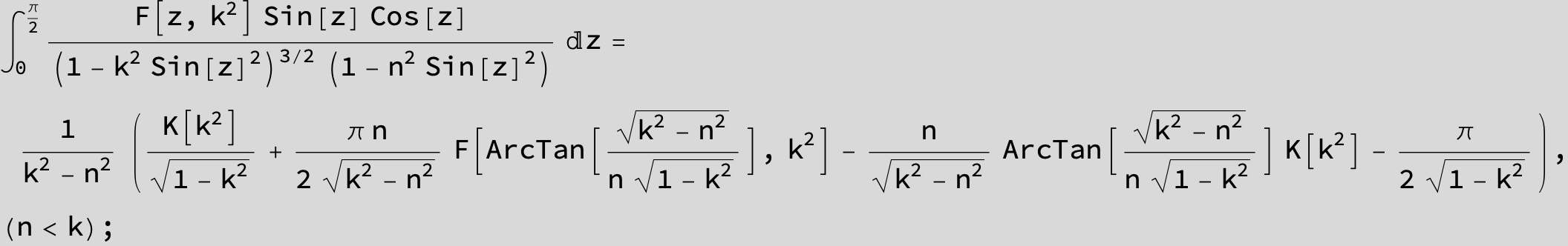
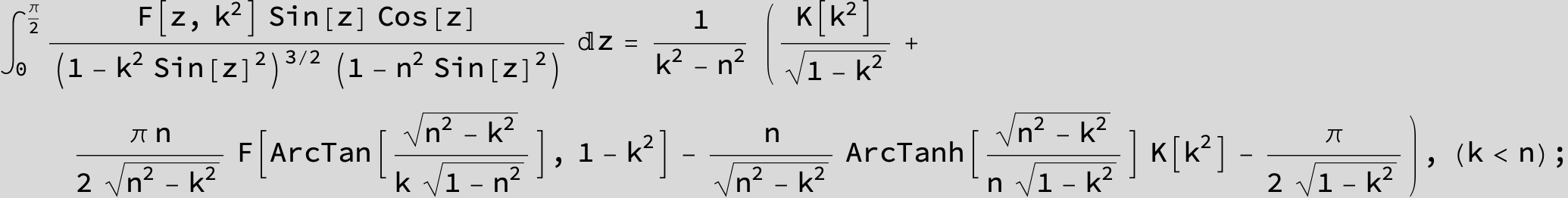
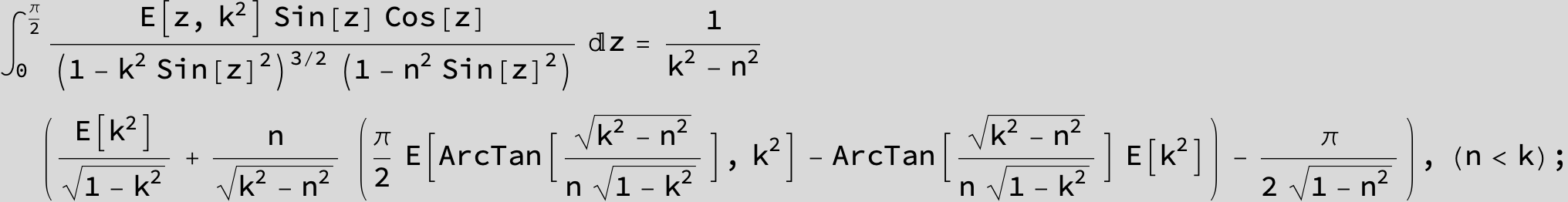
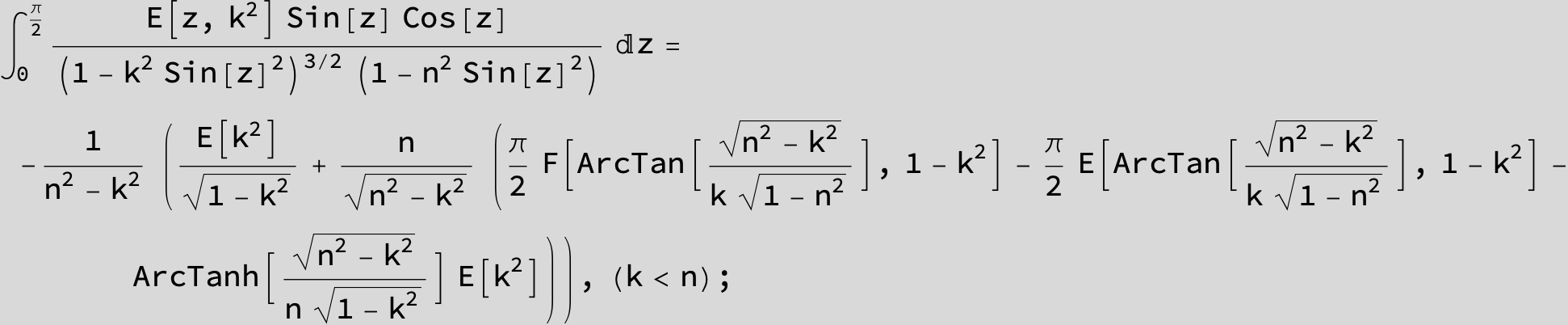
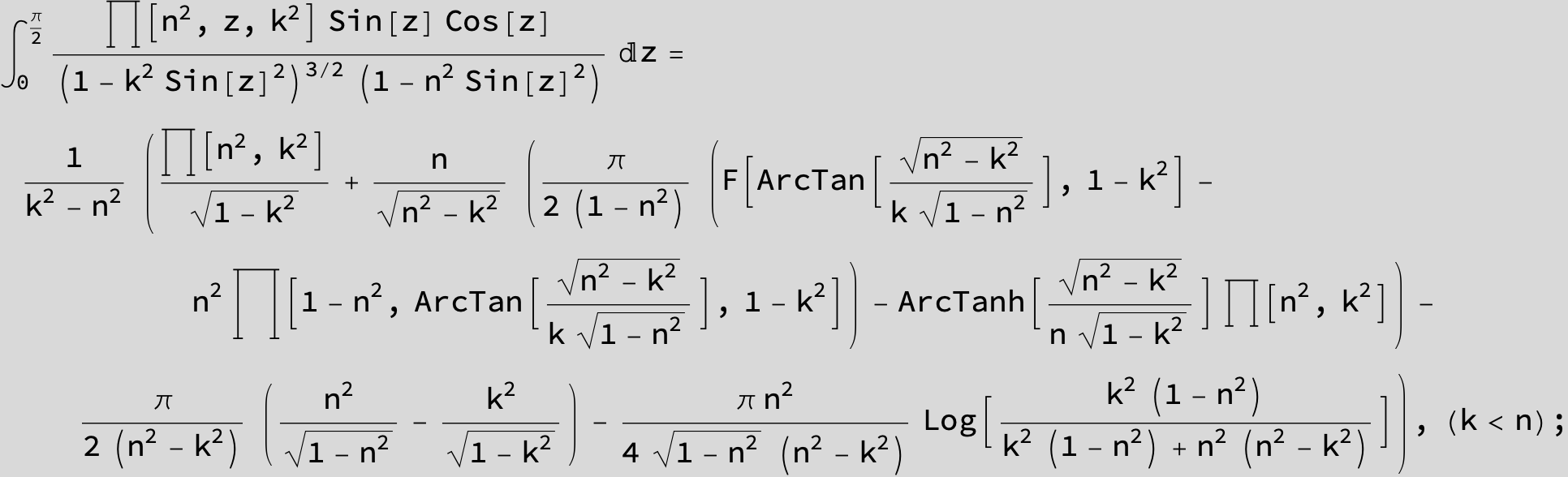
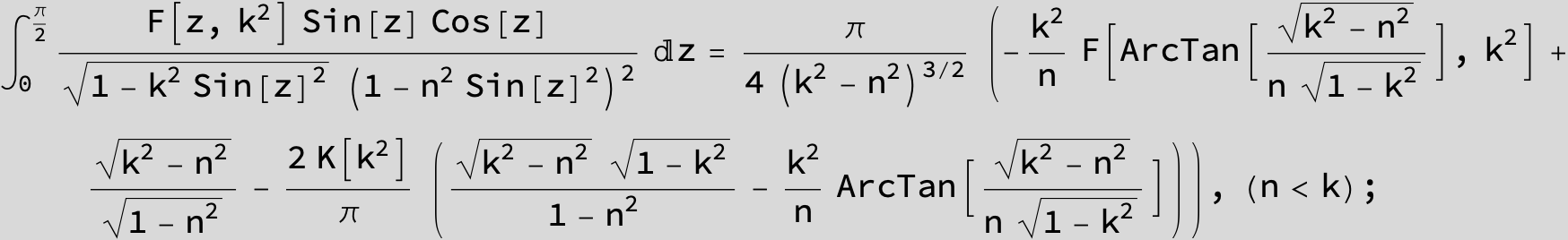
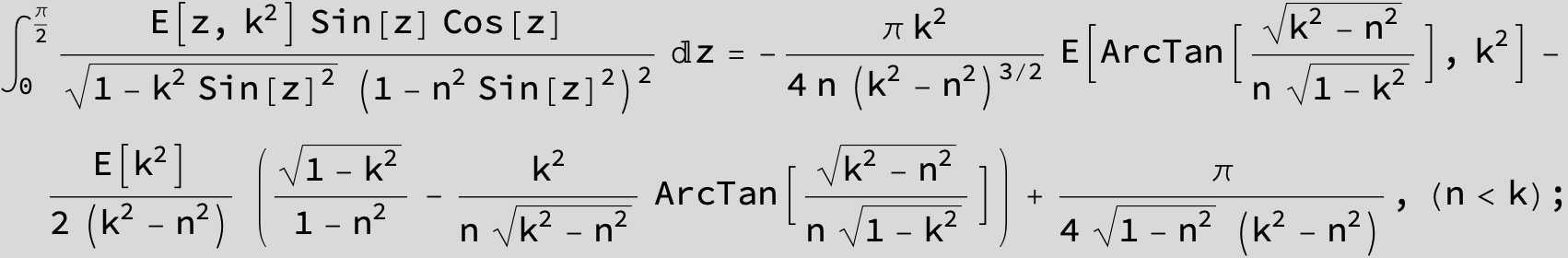
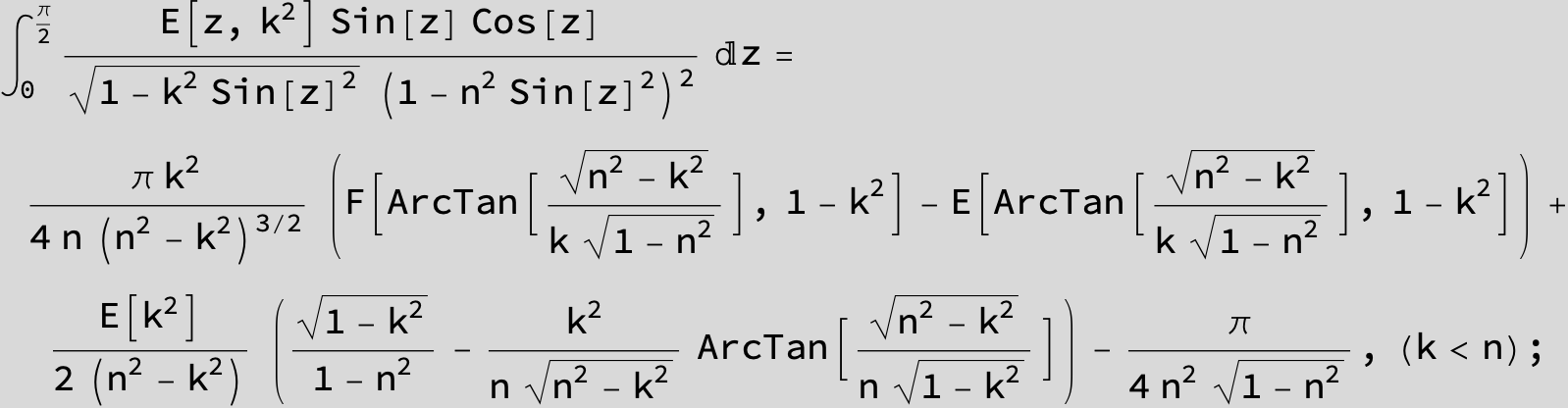
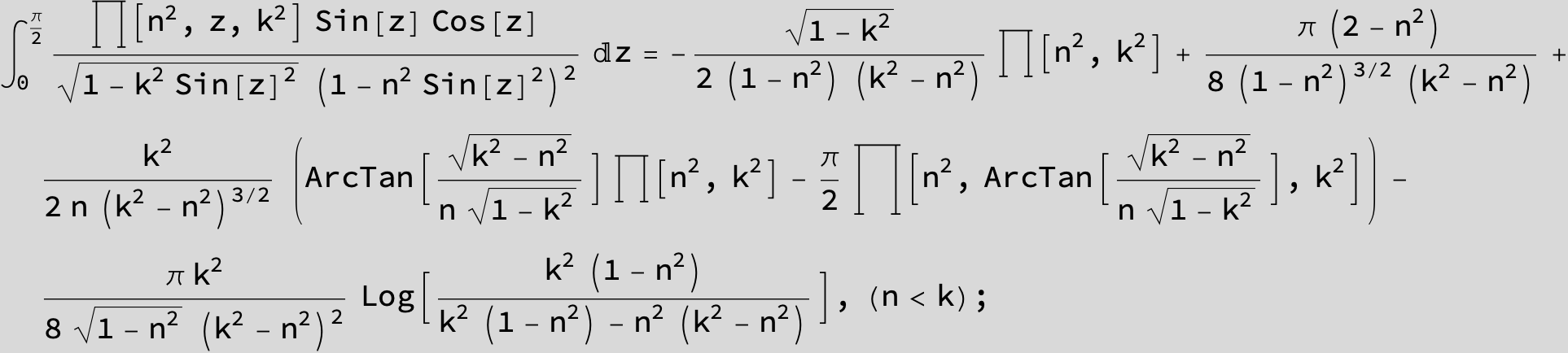
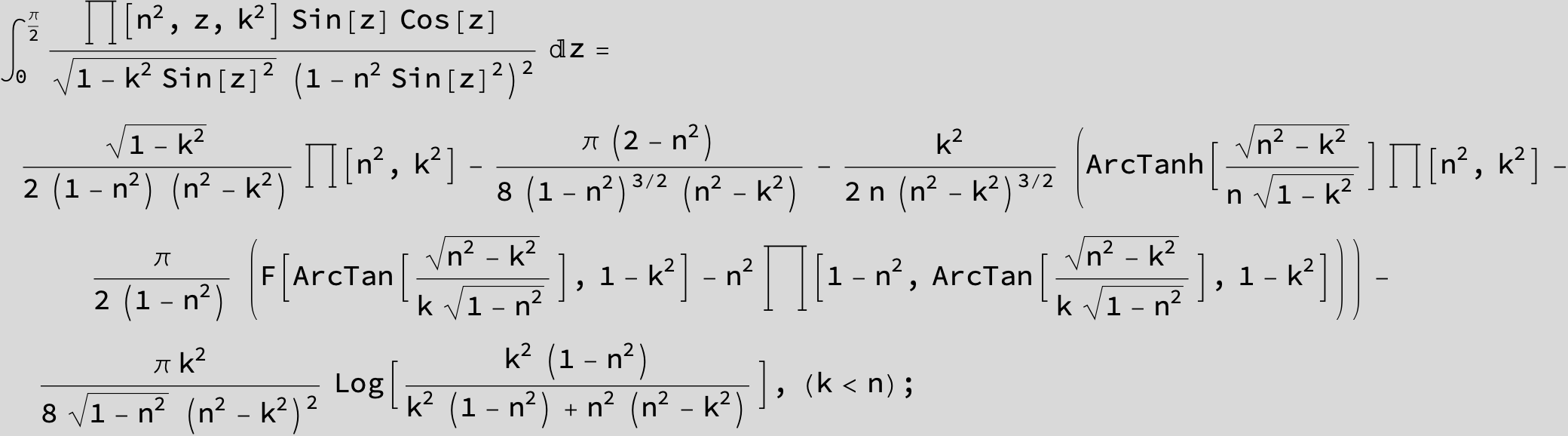
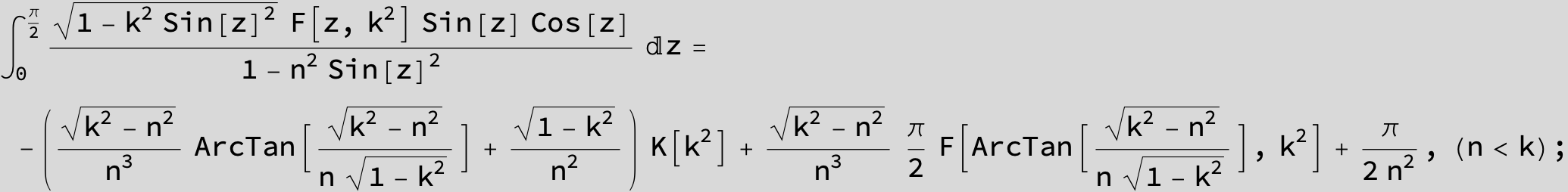
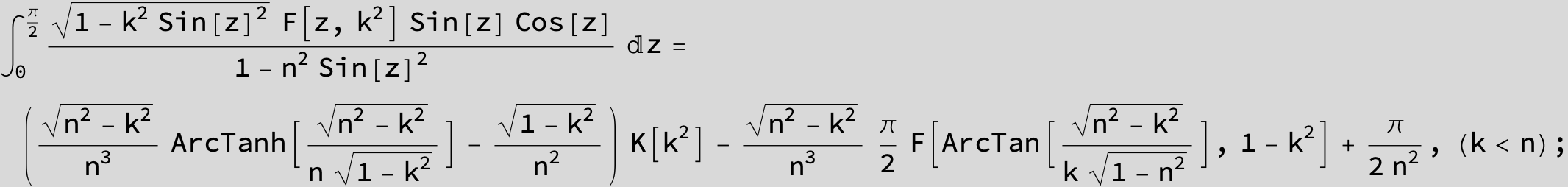
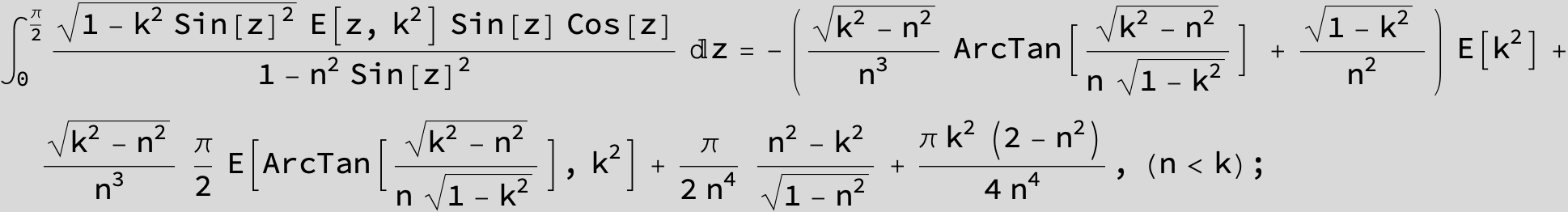
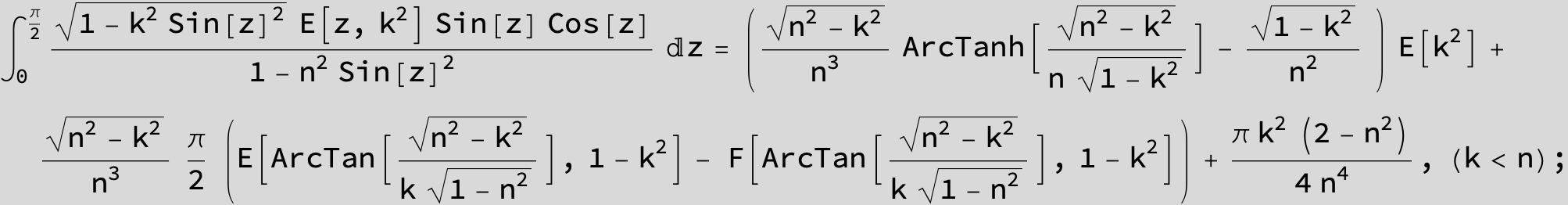
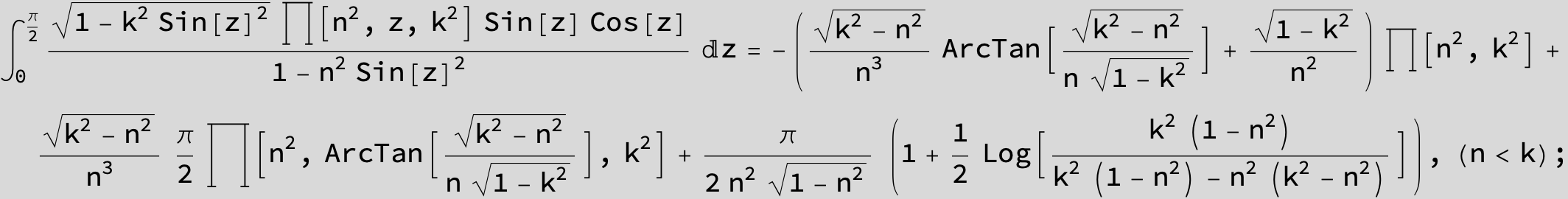
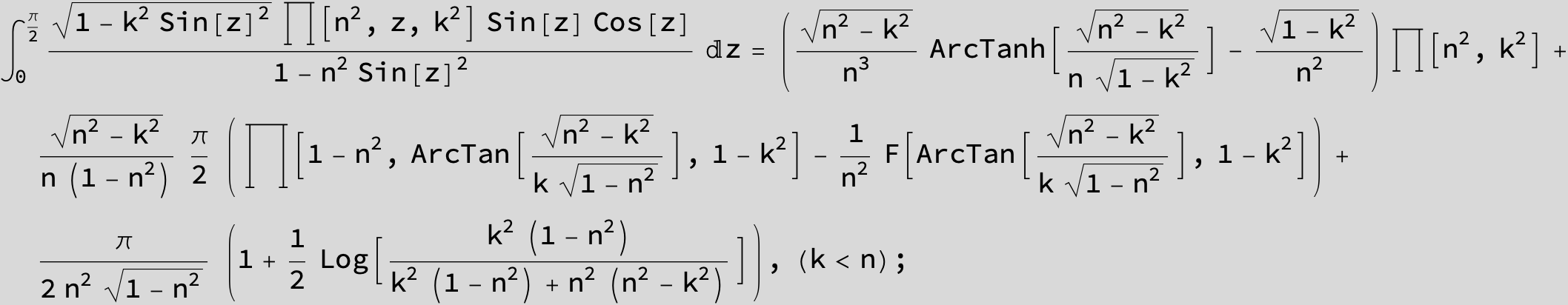
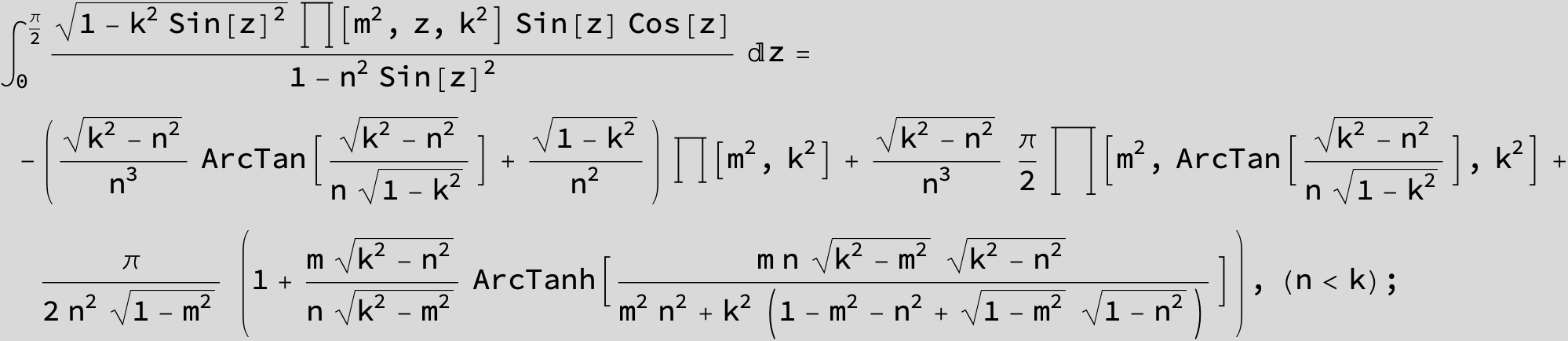
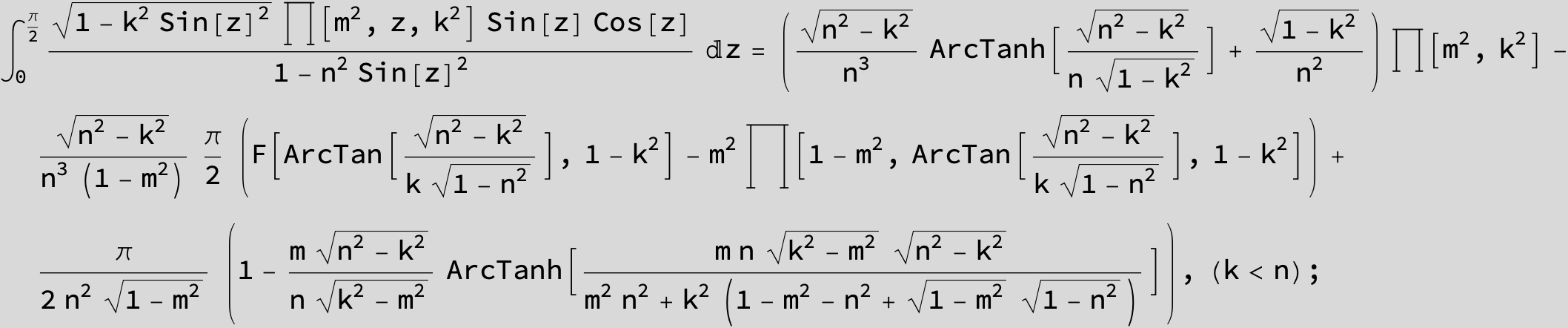
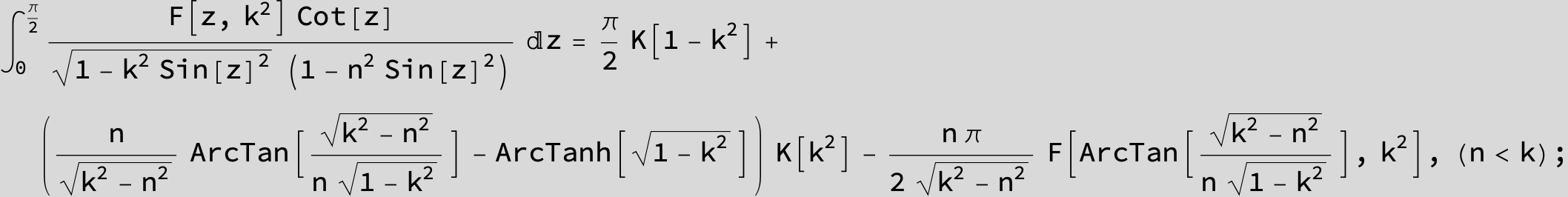
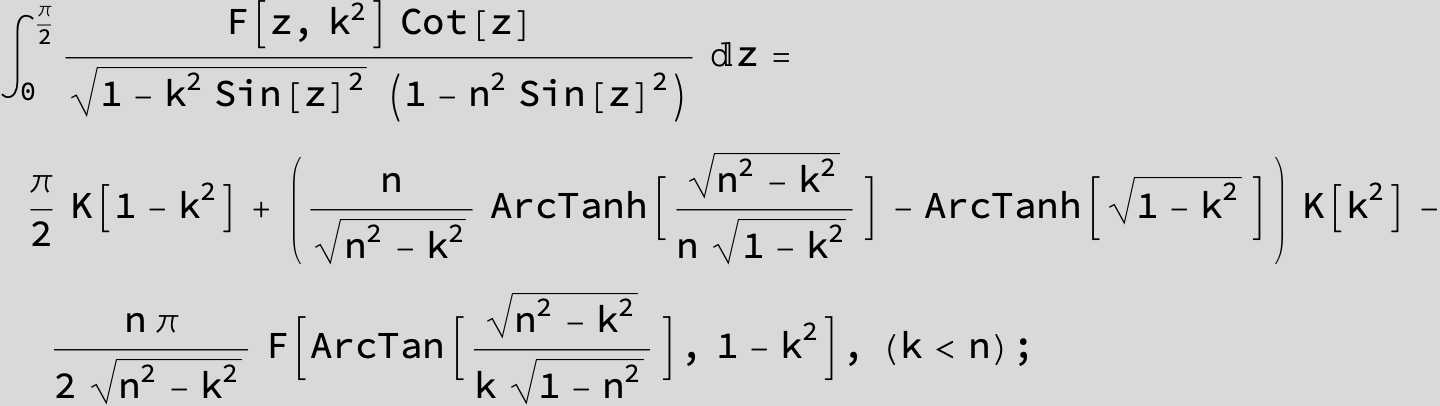
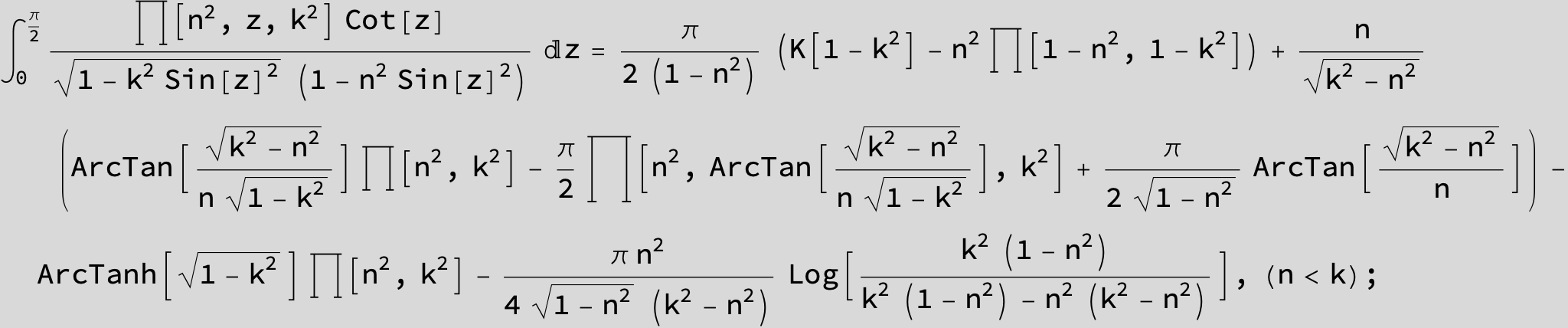
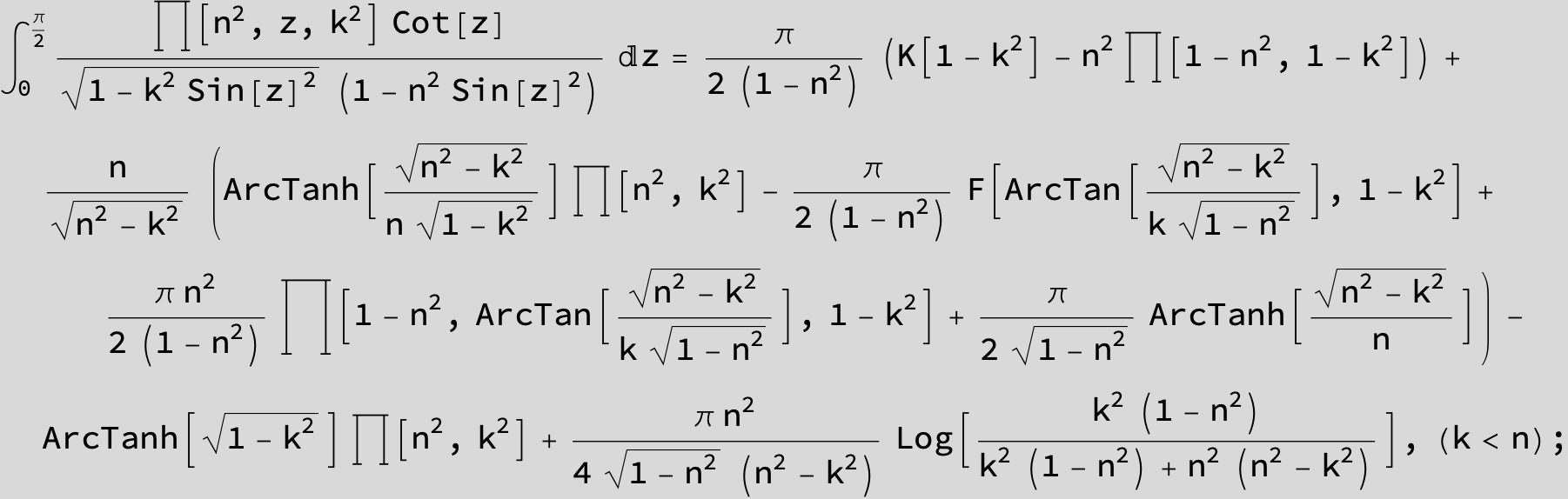
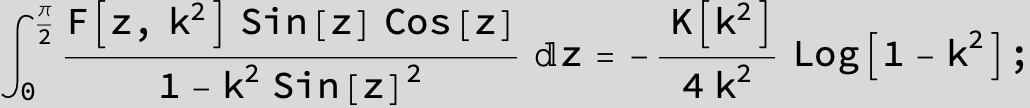
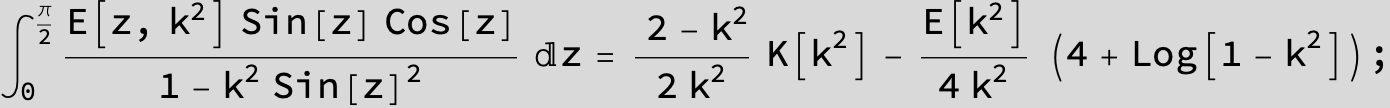
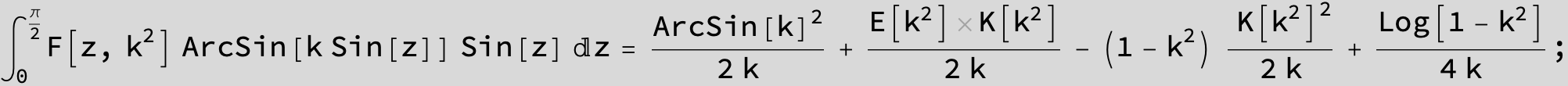
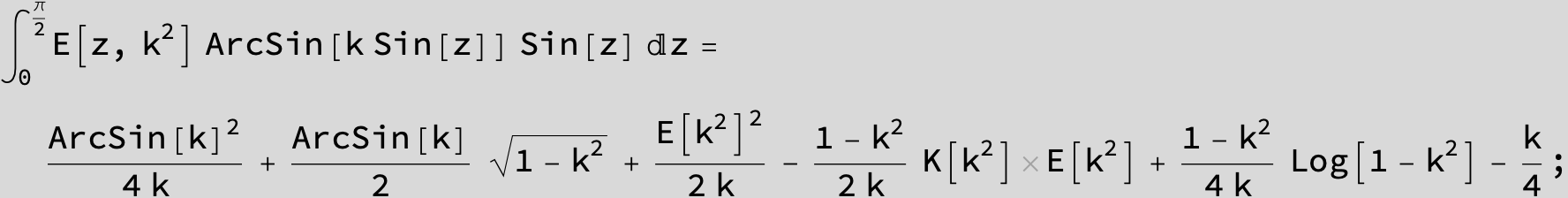
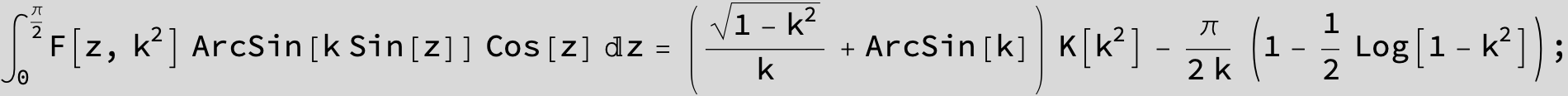
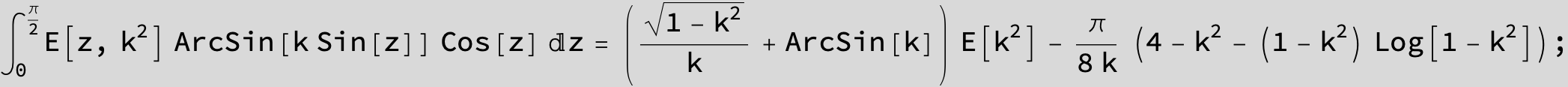
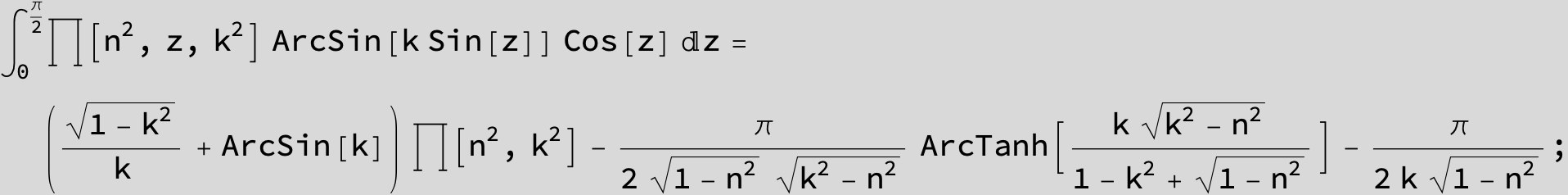
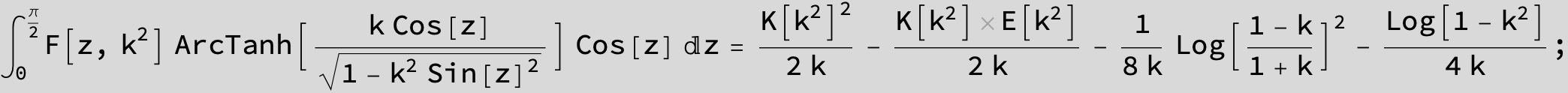
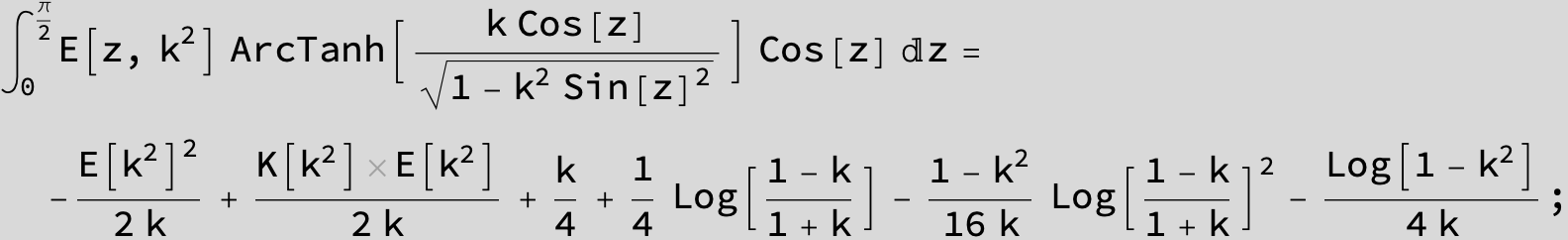
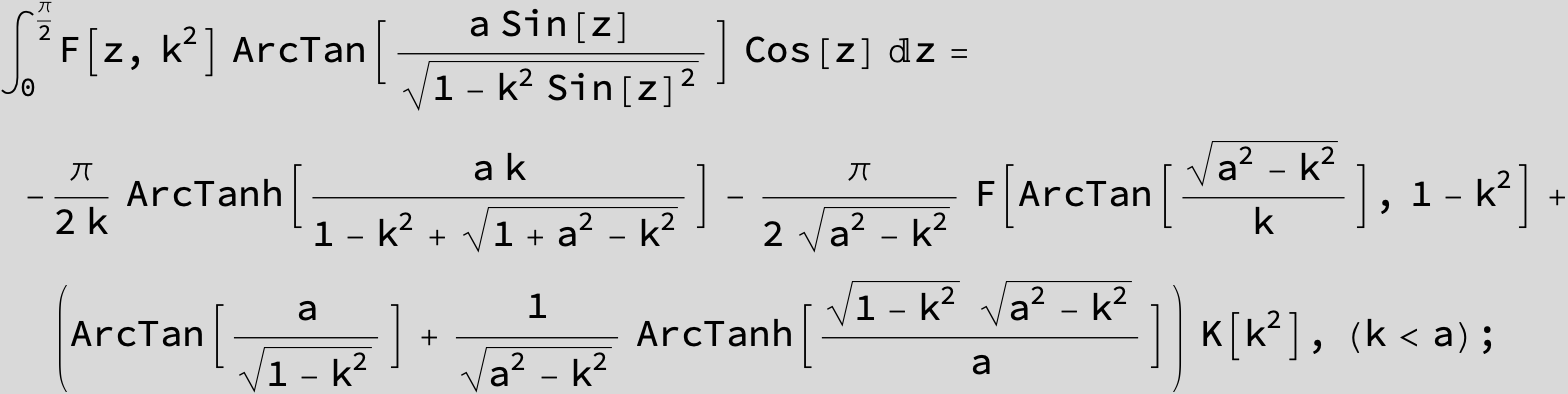
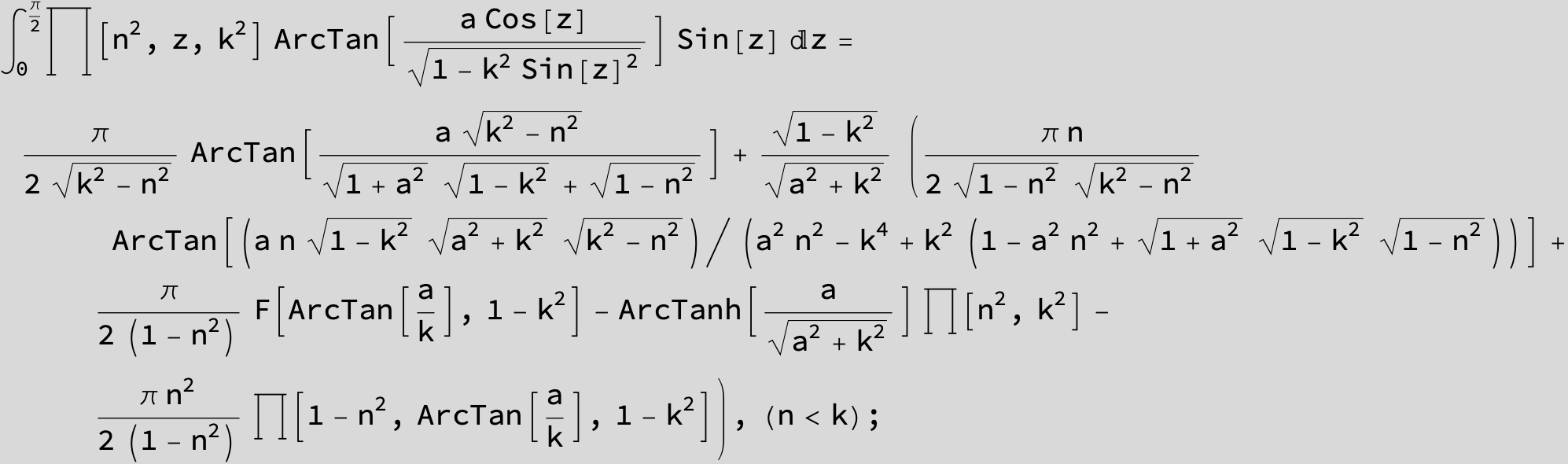
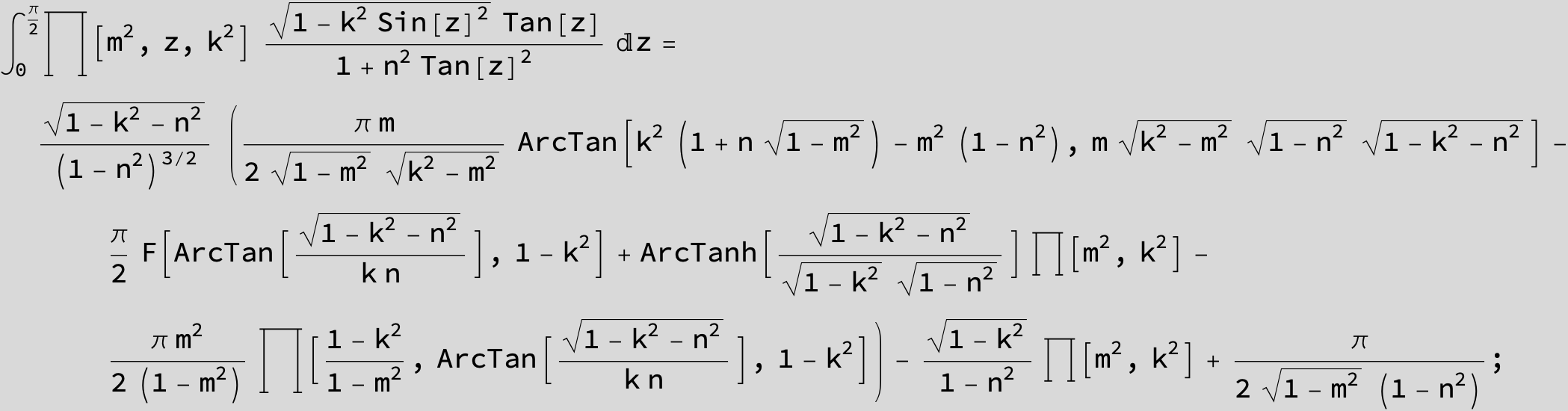
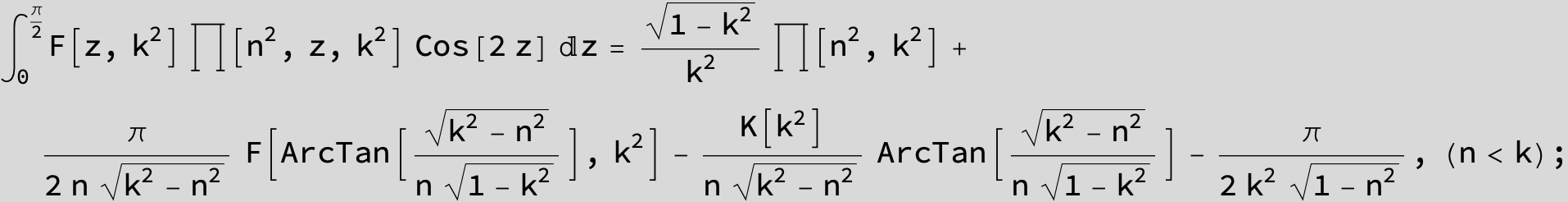
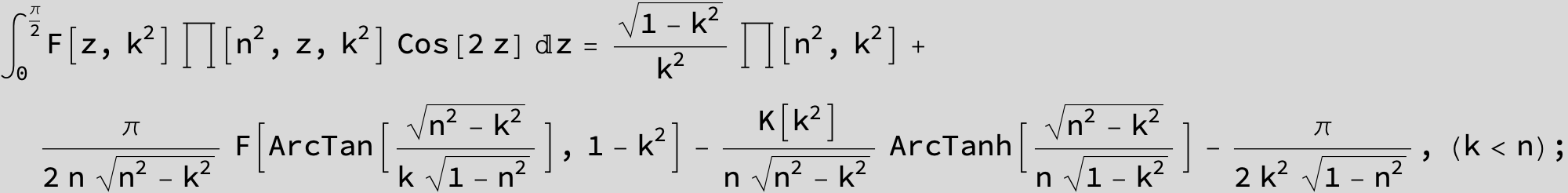
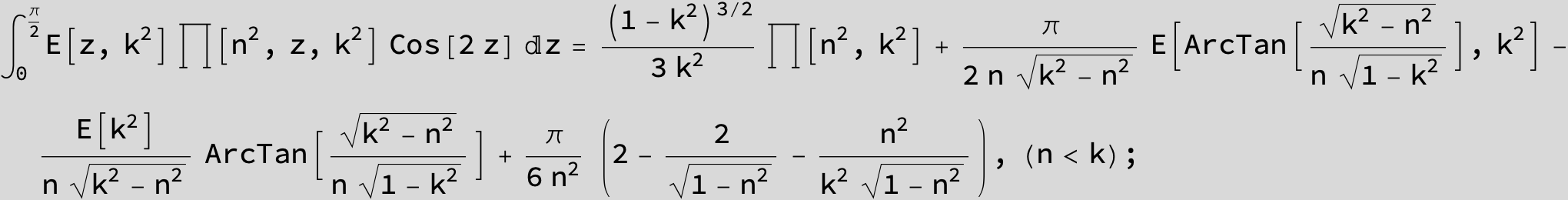
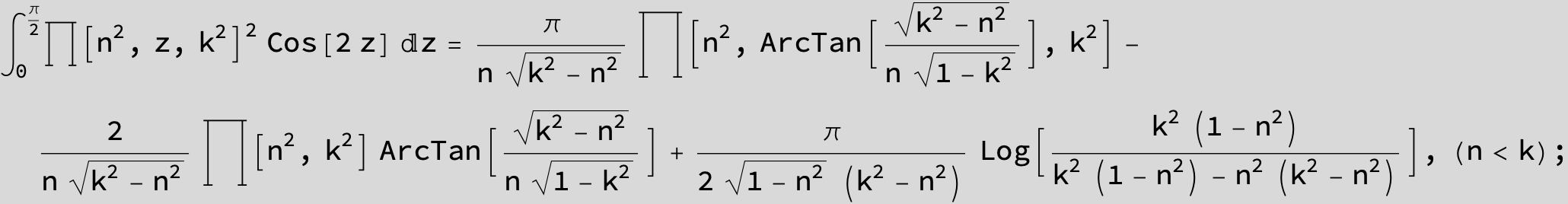
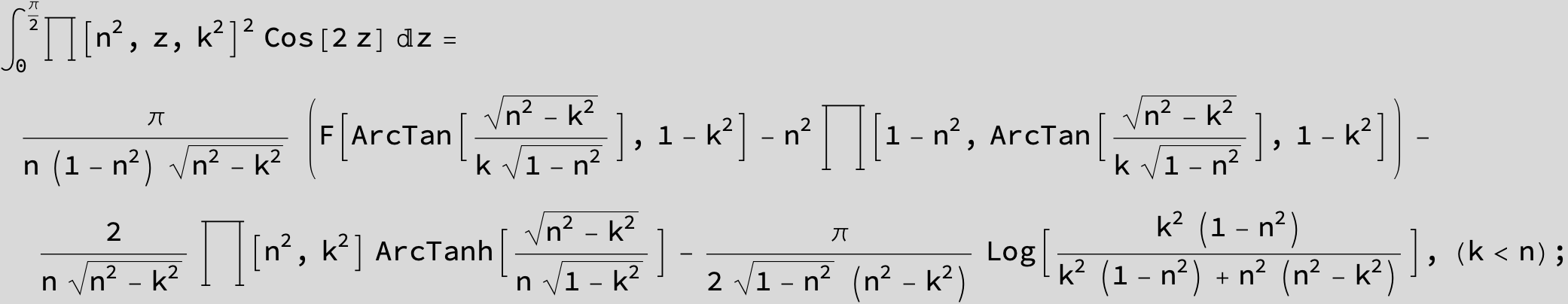
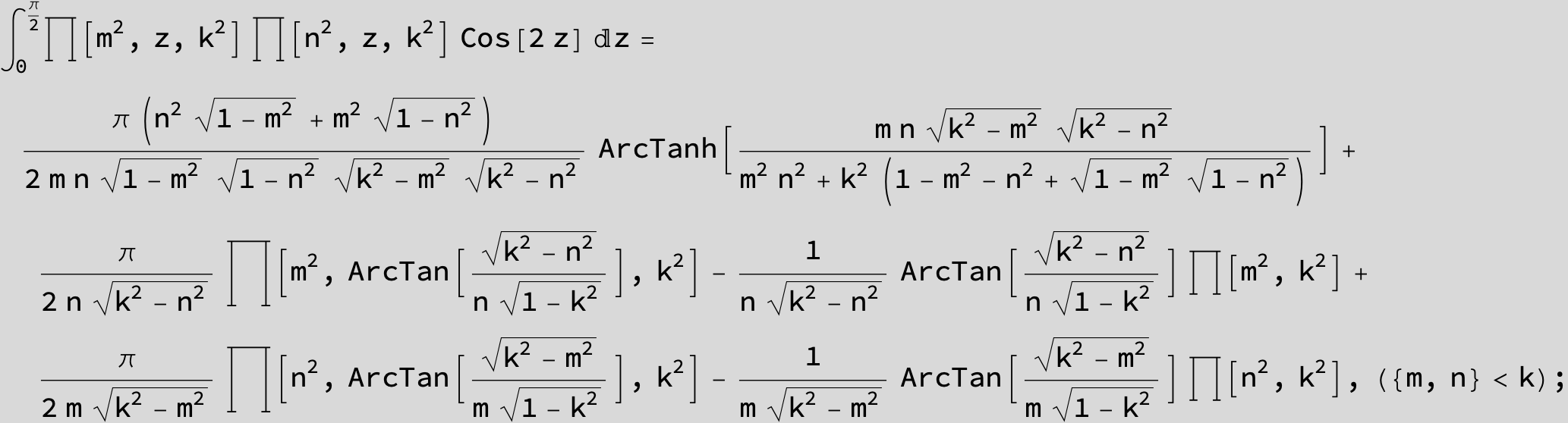
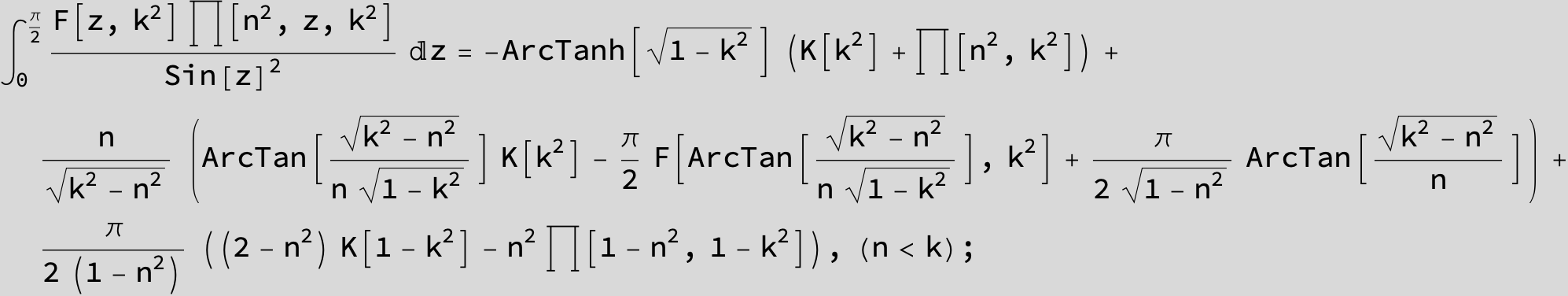
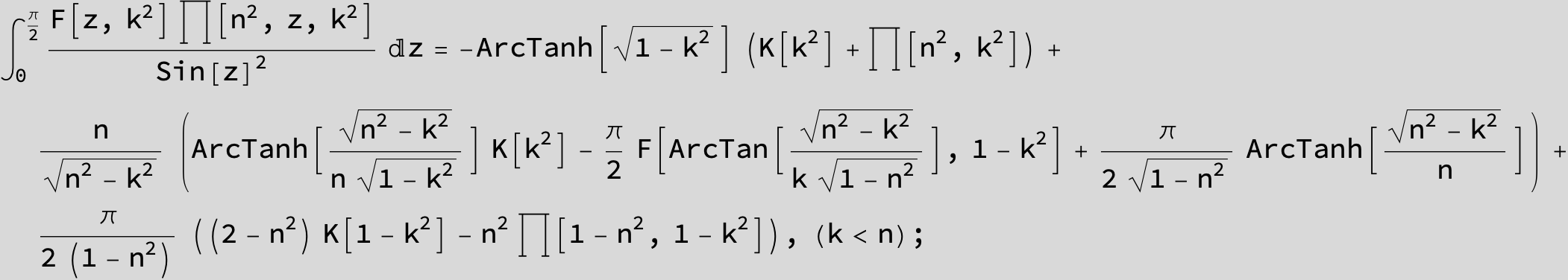
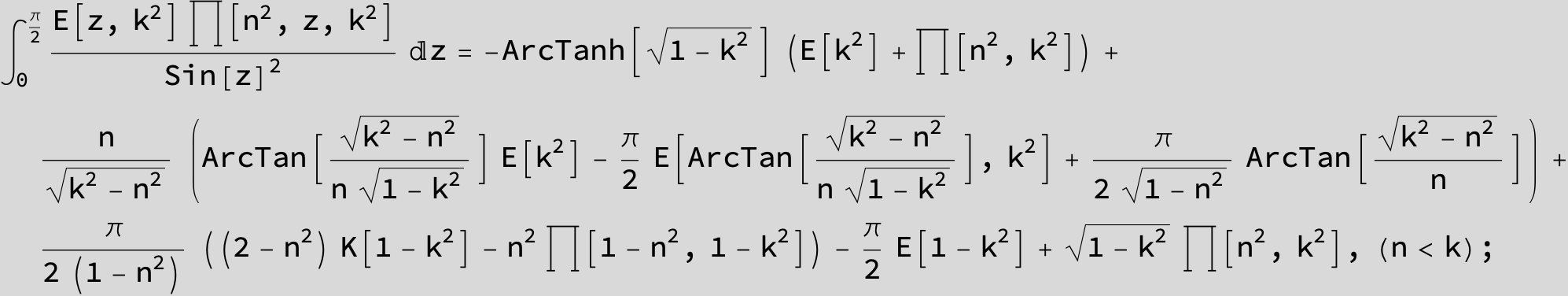
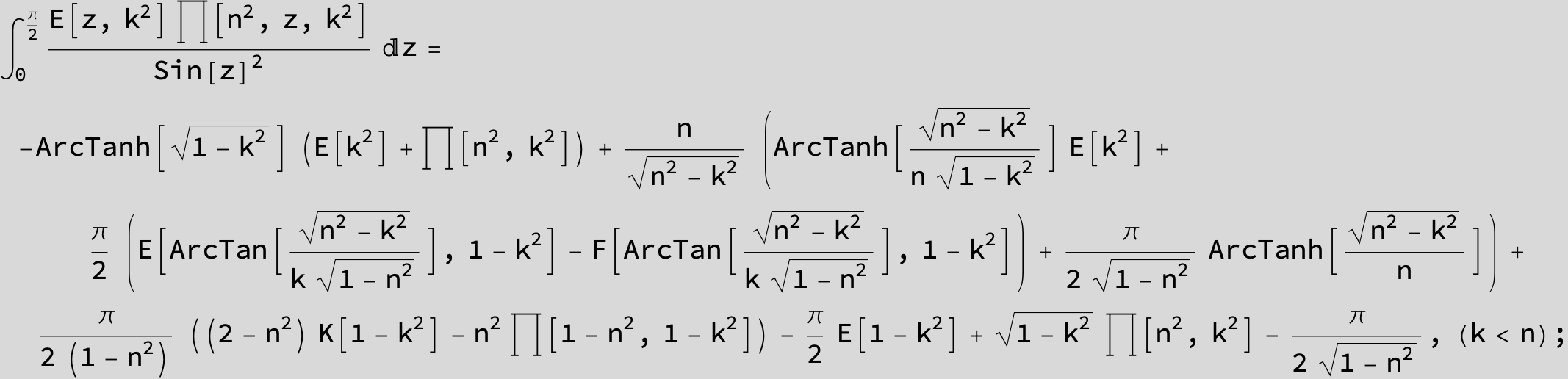
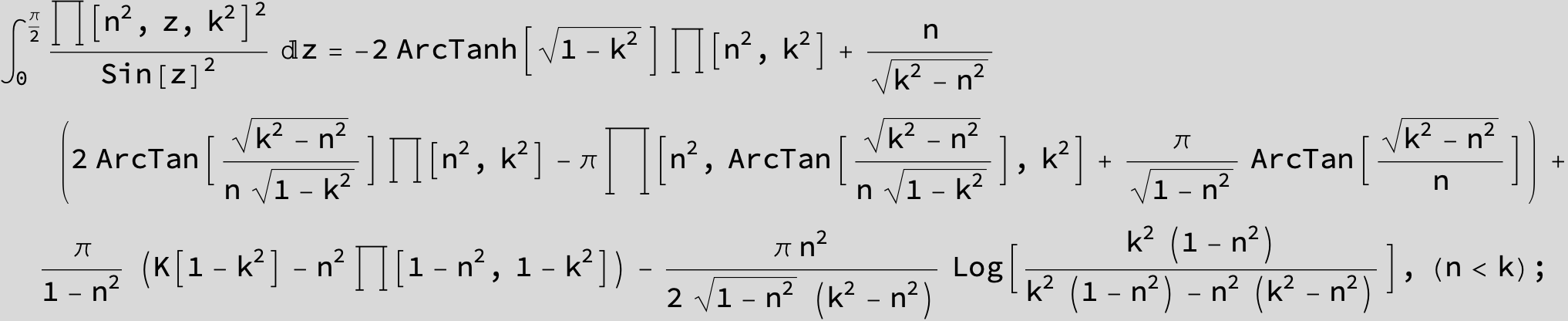
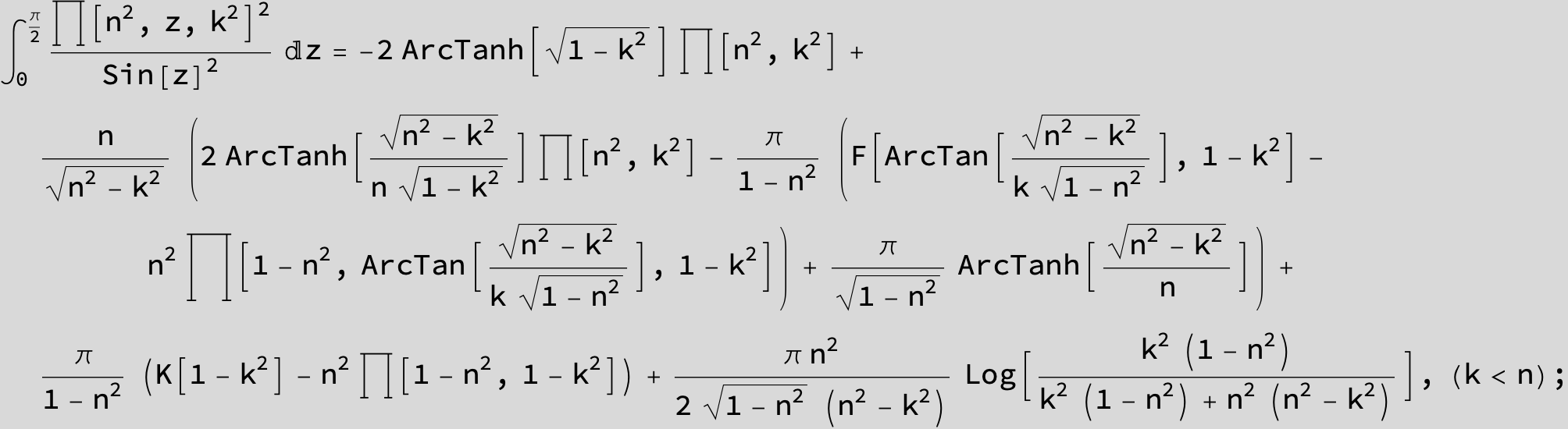
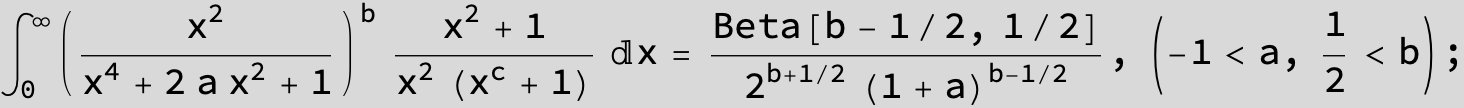
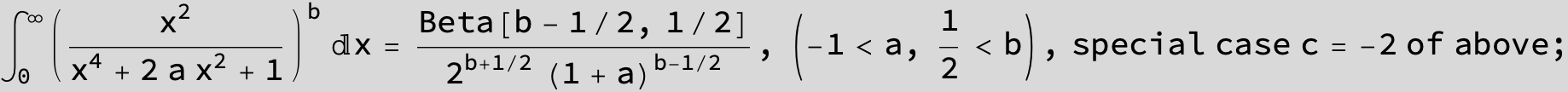
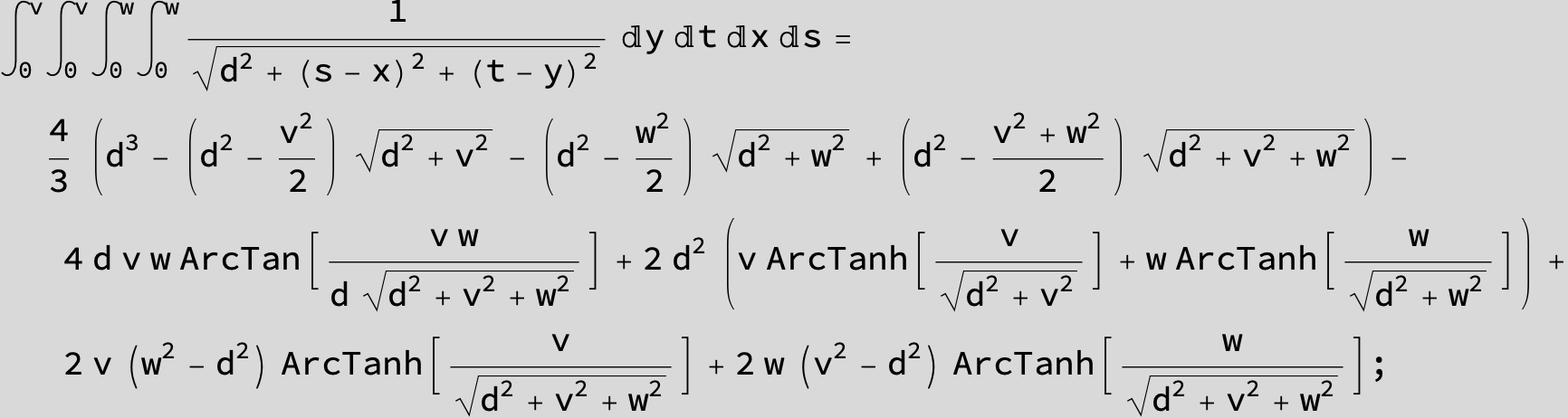
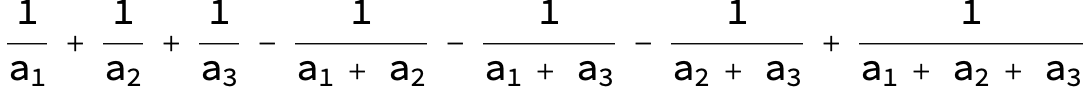
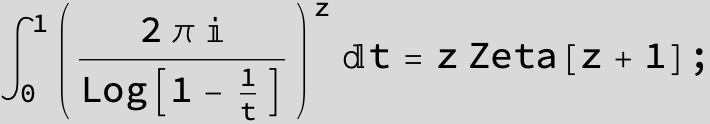
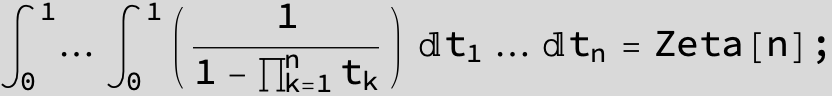
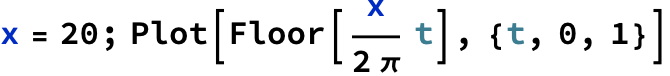
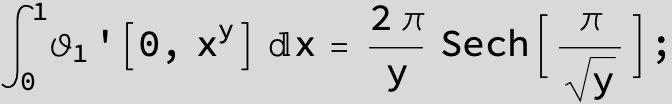
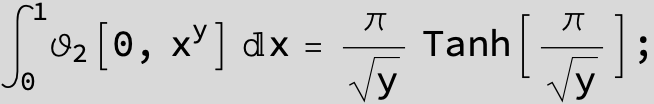
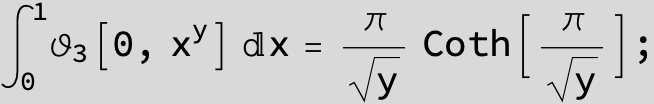
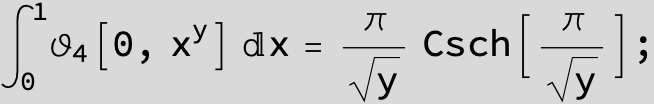
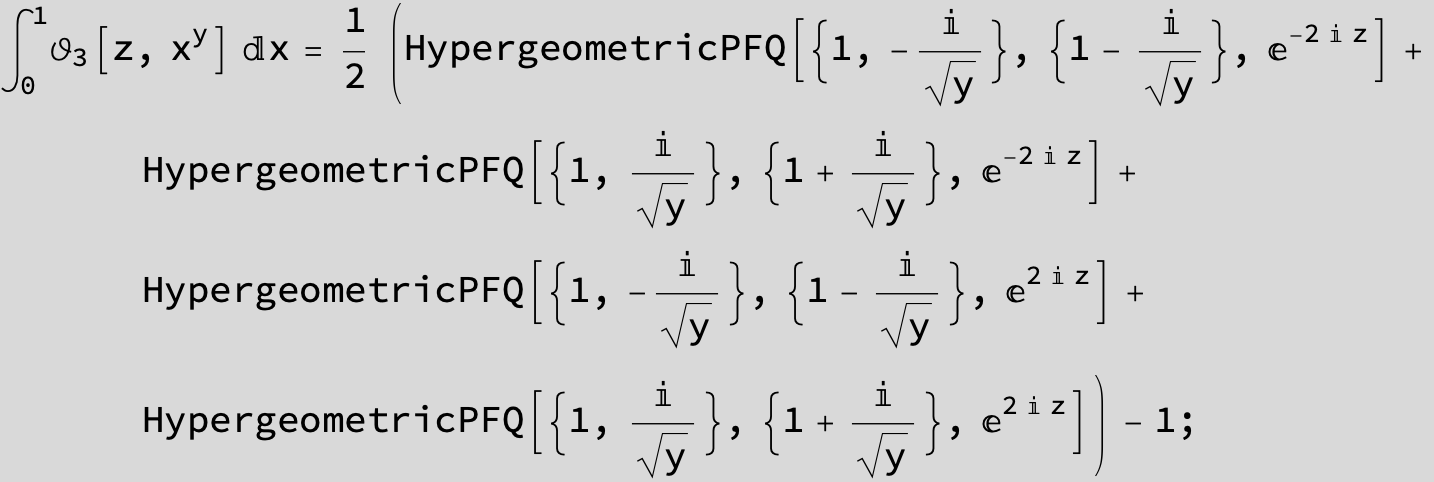
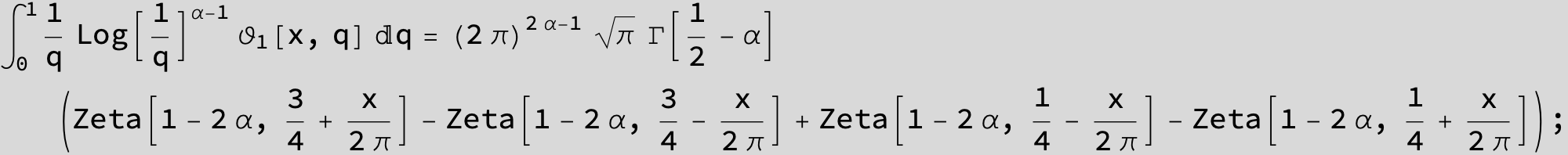
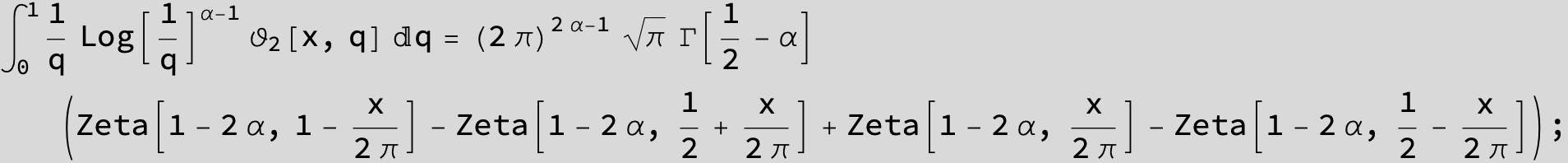
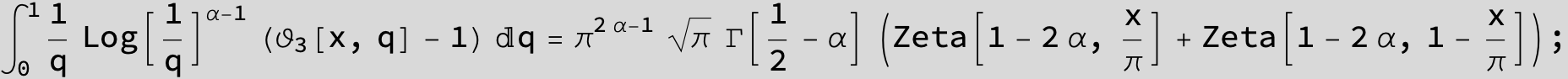
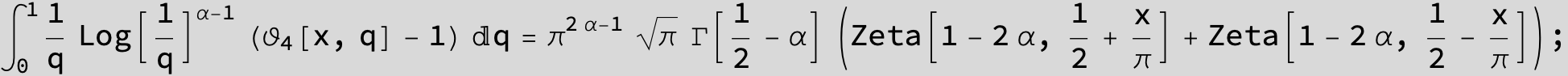
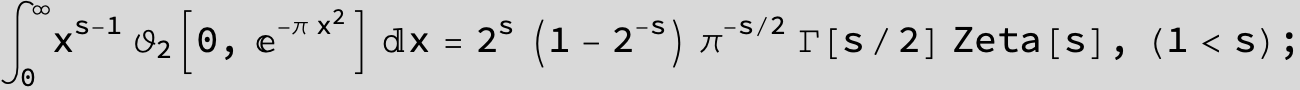
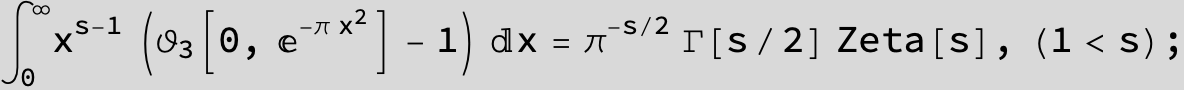
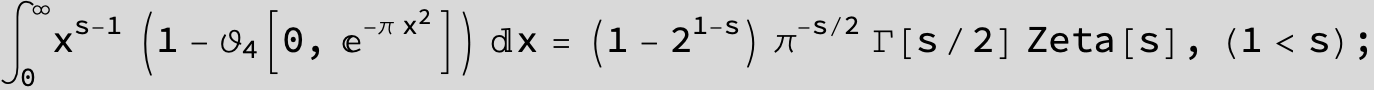
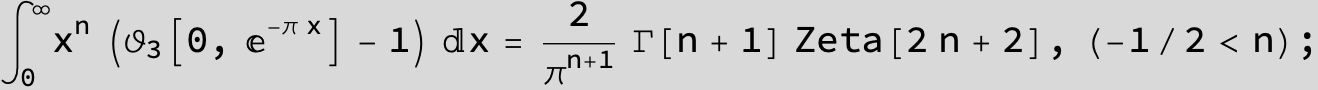
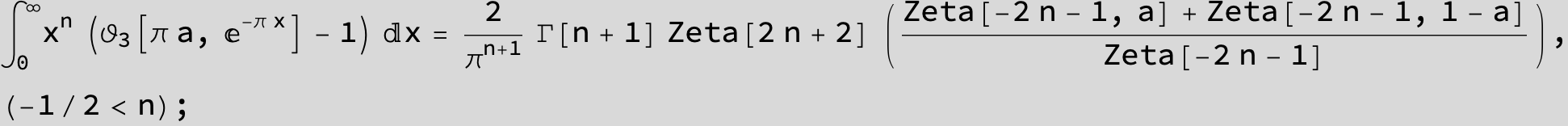
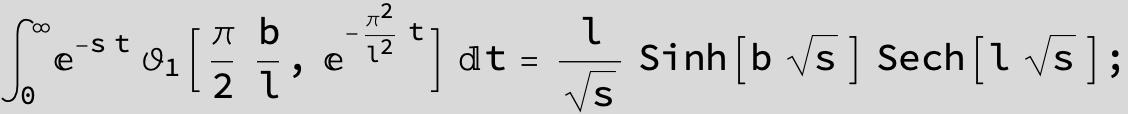
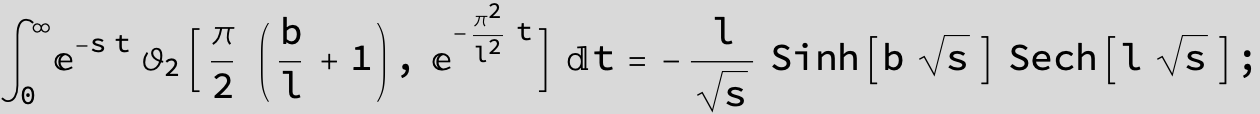
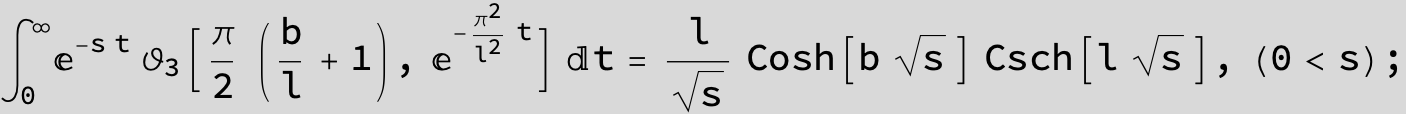
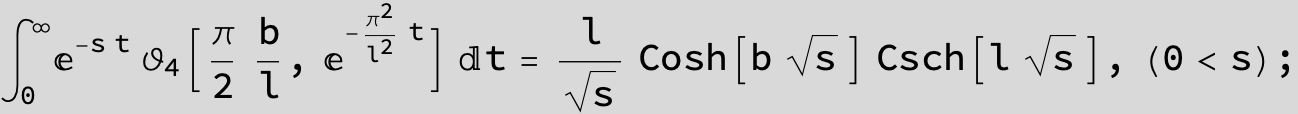
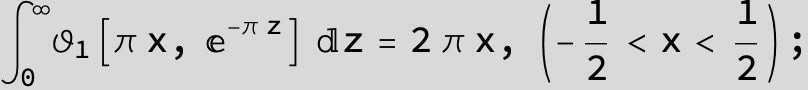
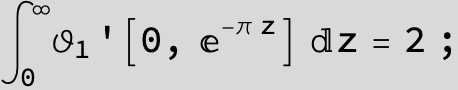
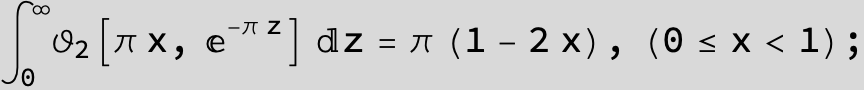
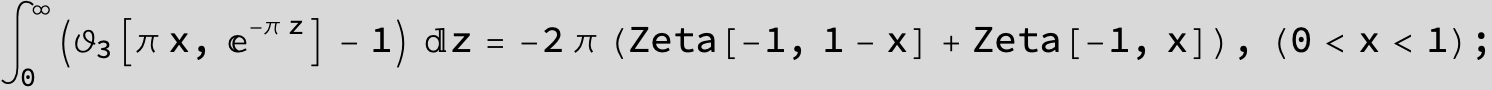
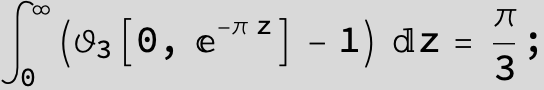
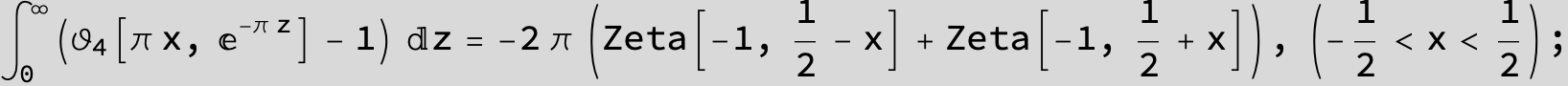
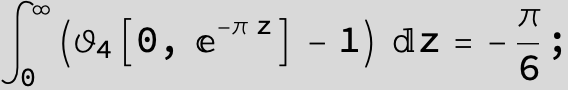
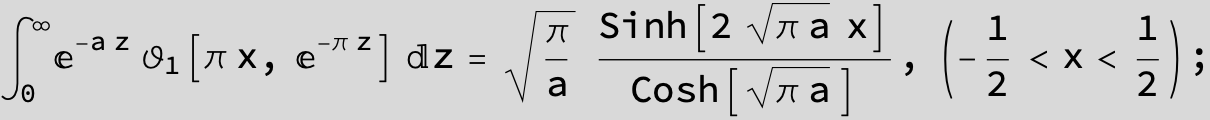
Master formula of Boros and Moll:

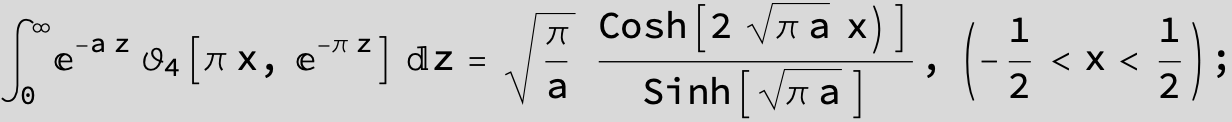
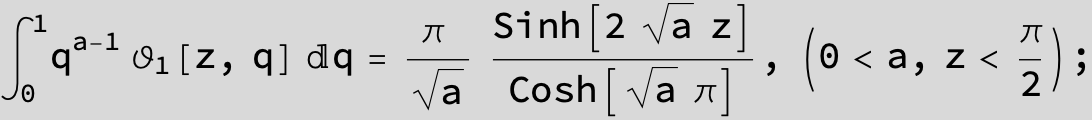
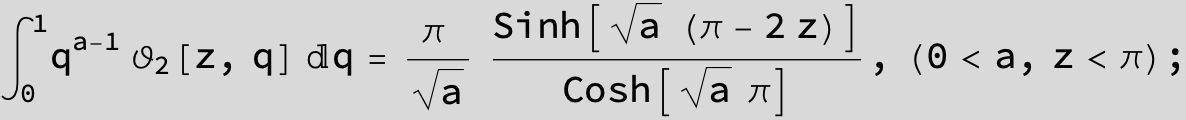
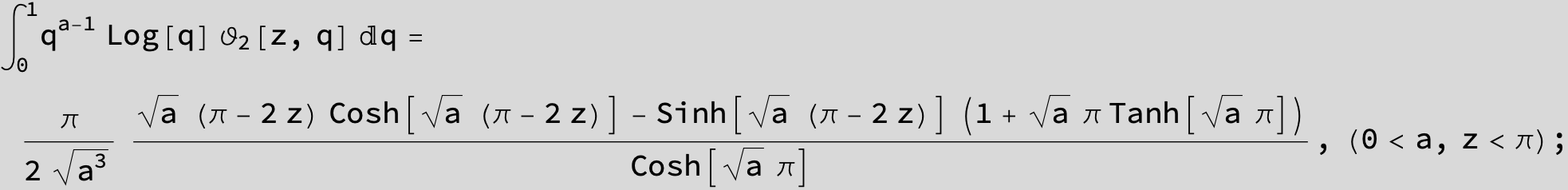
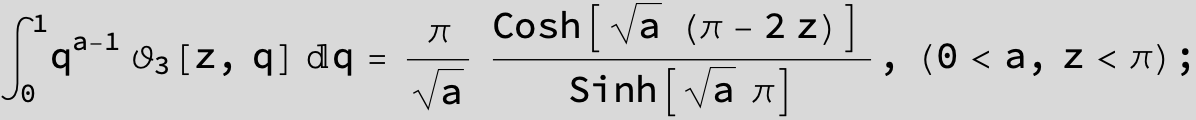
Here the result is a threefold sum shown in Mathematica syntax:
KSubsets[aList, k] is in Package DiscreteMath`Combinatorica` and gives a list of all subsets with k elements of aList .
For n=3 the sum is .
<<DiscreteMath`Combinatorica`

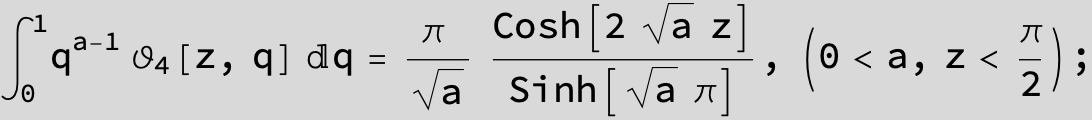
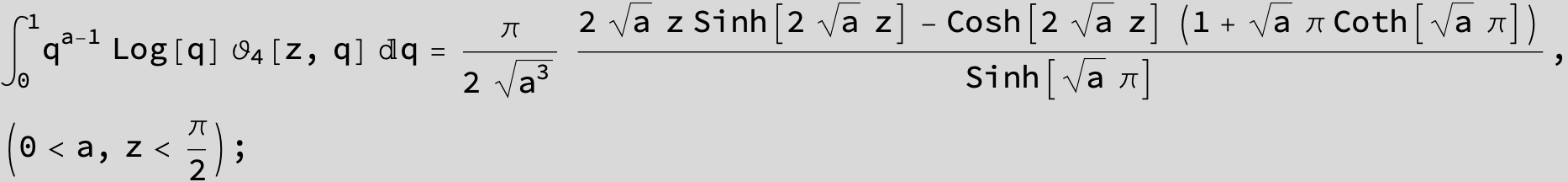
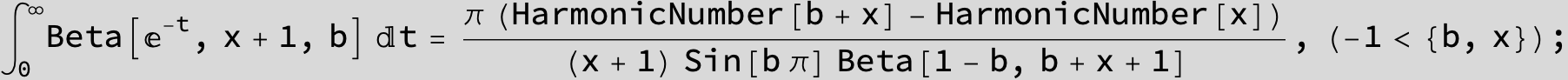
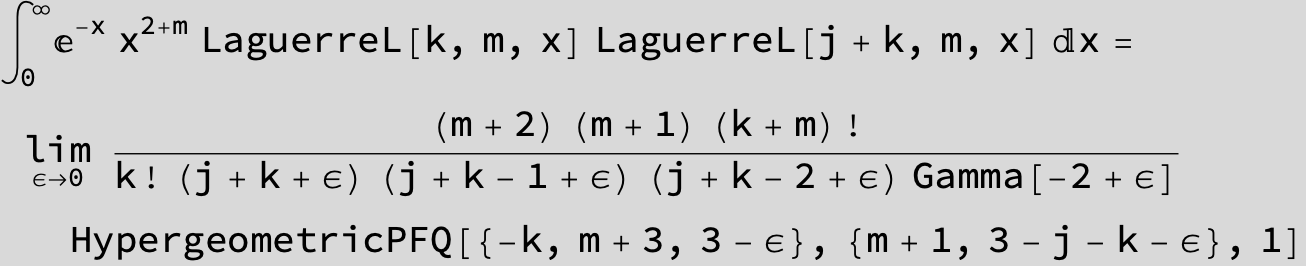
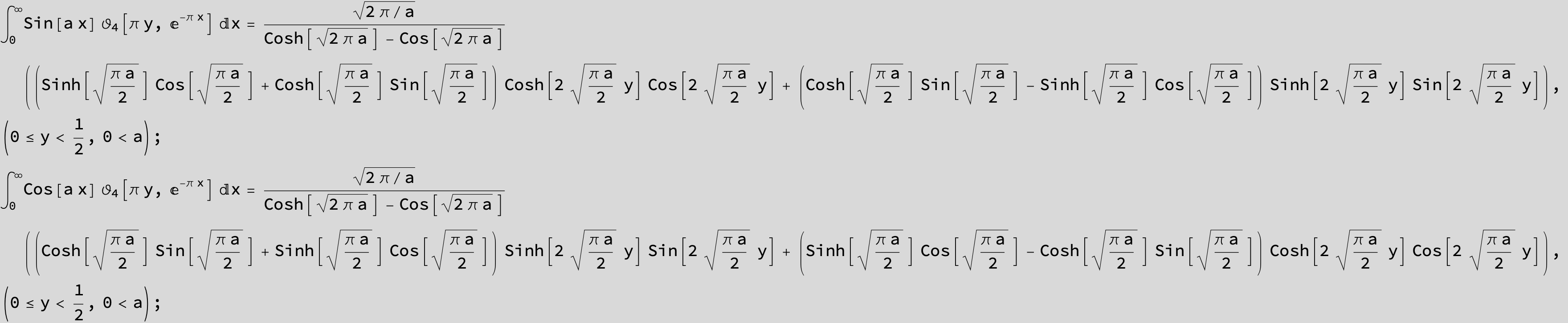
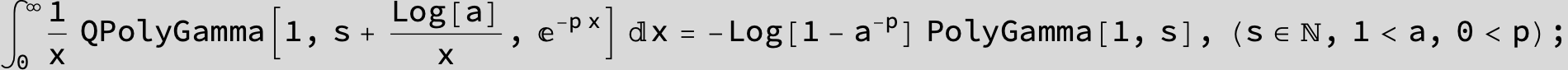
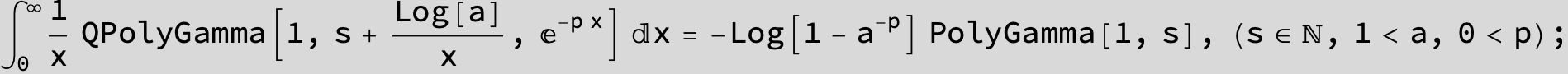
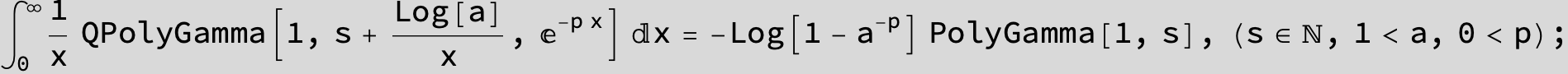
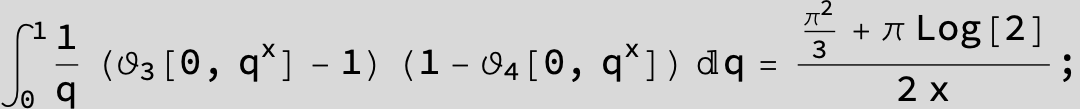
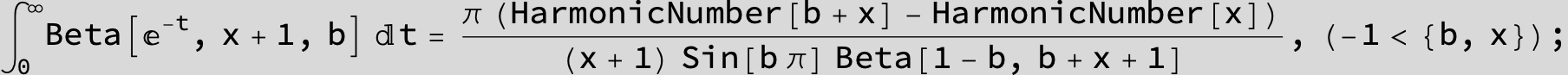
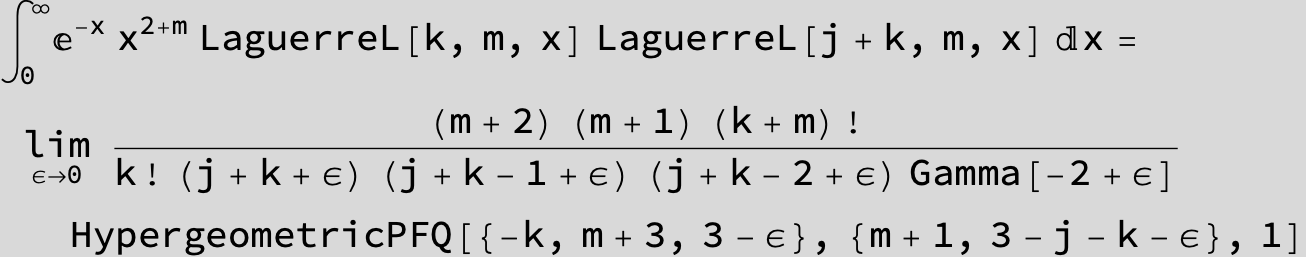
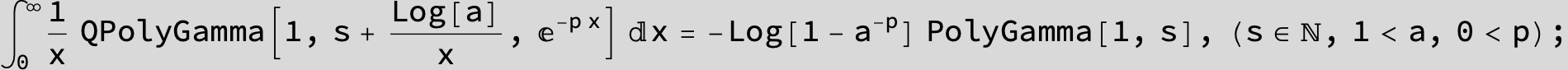
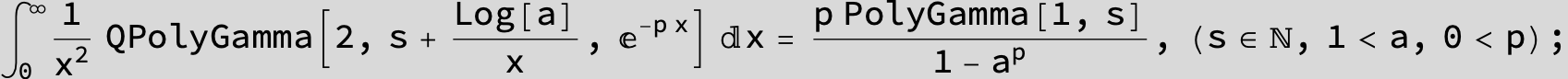
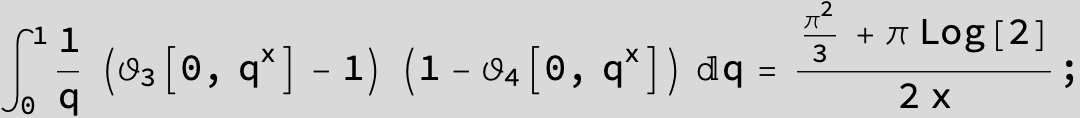
use  Γ[1 - t] Γ[t] = π Csc[π t]

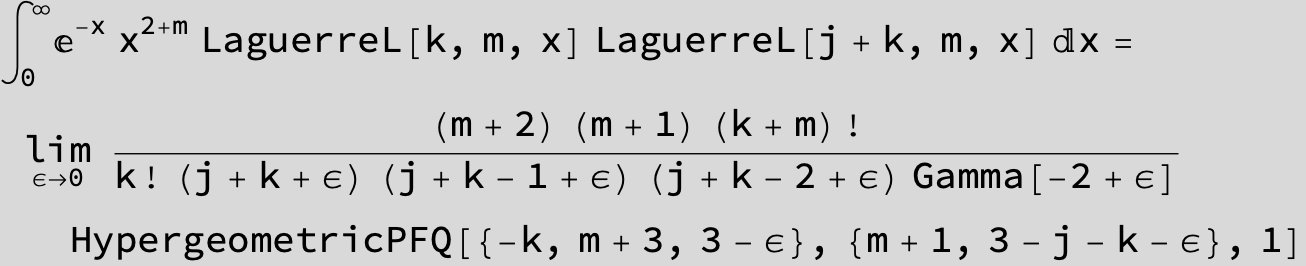
See below Mariusz's integrals that I was able to verify numerically :